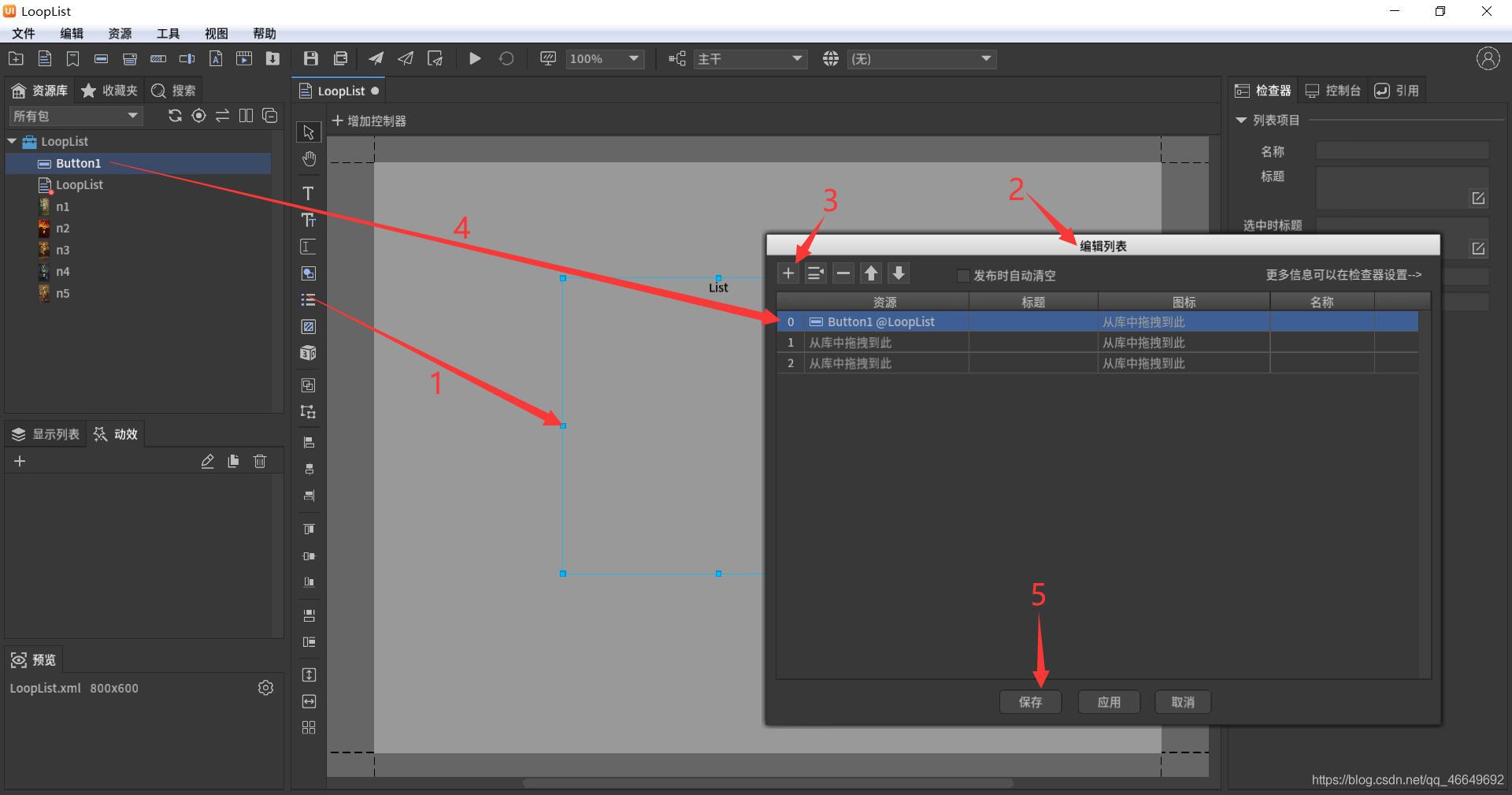
Problems and solutions of robust estimation in rtklib single point location spp

Problem description
stay spp When robust estimation is applied in , After calculating the observed value, the residual error v Covariance matrix of , There is a problem ,Qvv The diagonal element has a negative value .
First , I suspect there is something wrong with my code , The next step is debugging , stay vs The debugging matrix is really impressive .
secondly , I will spp Coefficient matrix in H、 Constant matrix l、 Covariance matrix Qxx、 Parameter vector dx It's printed , stay matlab Verification comparison .
1、matlab Print the above matrix

>> H=[       0.497179       -0.767231        0.405178        1.000000        0.000000        0.000000        0.000000;
       0.954274        0.112689       -0.276879        1.000000        0.000000        0.000000        0.000000;
       0.387339       -0.481553       -0.786178        1.000000        0.000000        0.000000        0.000000;
      -0.580737       -0.519400       -0.626872        1.000000        0.000000        0.000000        0.000000;
      -0.287620       -0.601084       -0.745636        1.000000        0.000000        0.000000        0.000000;
       0.394442       -0.847597       -0.354957        1.000000        0.000000        0.000000        0.000000;
       0.479621       -0.224119       -0.848371        1.000000        0.000000        0.000000        0.000000;
      -0.266211       -0.887121        0.377026        1.000000        0.000000        0.000000        0.000000;
       0.000000        0.000000        0.000000        0.000000        1.000000        0.000000        0.000000;
       0.000000        0.000000        0.000000        0.000000        0.000000        1.000000        0.000000;
       0.000000        0.000000        0.000000        0.000000        0.000000        0.000000        1.000000];
>> Q=[       1.444742       -1.205538       -0.559907       -1.256723        0.000000        0.000000        0.000000;
      -1.205538        4.239855        1.510516        3.308947        0.000000        0.000000        0.000000;
      -0.559907        1.510516        1.847995        1.891790        0.000000        0.000000        0.000000;
      -1.256723        3.308947        1.891790        3.215663        0.000000        0.000000        0.000000;
       0.000000        0.000000        0.000000        0.000000        0.010000        0.000000        0.000000;
       0.000000        0.000000        0.000000        0.000000        0.000000        0.010000        0.000000;
       0.000000        0.000000        0.000000        0.000000        0.000000        0.000000        0.010000];
>> dx=[       0.000009
      -0.000020
      -0.000022
      -0.000041
       0.000000
       0.000000
       0.000000];
>>  l=[0.123075
       0.433912
       0.828791
       0.067140
       0.026320
      -0.289038
      -0.862615
      -0.198928
       0.000000
       0.000000
       0.000000];
>> H'

ans =

  Columns 1 through 8

   0.497179000000000   0.954274000000000   0.387339000000000  -0.580737000000000  -0.287620000000000   0.394442000000000   0.479621000000000  -0.266211000000000
  -0.767231000000000   0.112689000000000  -0.481553000000000  -0.519400000000000  -0.601084000000000  -0.847597000000000  -0.224119000000000  -0.887121000000000
   0.405178000000000  -0.276879000000000  -0.786178000000000  -0.626872000000000  -0.745636000000000  -0.354957000000000  -0.848371000000000   0.377026000000000
   1.000000000000000   1.000000000000000   1.000000000000000   1.000000000000000   1.000000000000000   1.000000000000000   1.000000000000000   1.000000000000000
                   0                   0                   0                   0                   0                   0                   0                   0
                   0                   0                   0                   0                   0                   0                   0                   0
                   0                   0                   0                   0                   0                   0                   0                   0

  Columns 9 through 11

                   0                   0                   0
                   0                   0                   0
                   0                   0                   0
                   0                   0                   0
   1.000000000000000                   0                   0
                   0   1.000000000000000                   0
                   0                   0   1.000000000000000

>> H*Q*H'

ans =

  Columns 1 through 8

   1.332860500714645   0.645546014871716  -0.098580562413659  -0.064031507548390  -0.165752578512155   0.396295832699334  -0.141008818175153   1.168889713304825
   0.645546014871717   1.968804844653495   0.053246247795955  -0.005468449432181  -0.265950607478022  -0.319534503408733   0.574091433817809   0.243277031690377
  -0.098580562413659   0.053246247795955   0.357273653443425  -0.021840446651663   0.164659427109121   0.283415207166032   0.318871615198842  -0.284958778729781
  -0.064031507548390  -0.005468449432181  -0.021840446651663   1.072132904685670   0.641476084869937  -0.226446903091478   0.079281778351138   0.679077103029250
  -0.165752578512155  -0.265950607478023   0.164659427109121   0.641476084869937   0.515321629013082   0.067397424711531   0.125308500906703   0.247806596987045
   0.396295832699334  -0.319534503408734   0.283415207166032  -0.226446903091478   0.067397424711531   0.647339251042735   0.015423699735895   0.151774558340723
  -0.141008818175153   0.574091433817809   0.318871615198843   0.079281778351138   0.125308500906704   0.015423699735896   0.481685375510297  -0.331346855770643
   1.168889713304826   0.243277031690377  -0.284958778729780   0.679077103029250   0.247806596987045   0.151774558340723  -0.331346855770643   1.674731658216493
                   0                   0                   0                   0                   0                   0                   0                   0
                   0                   0                   0                   0                   0                   0                   0                   0
                   0                   0                   0                   0                   0                   0                   0                   0

  Columns 9 through 11

                   0                   0                   0
                   0                   0                   0
                   0                   0                   0
                   0                   0                   0
                   0                   0                   0
                   0                   0                   0
                   0                   0                   0
                   0                   0                   0
   0.010000000000000                   0                   0
                   0   0.010000000000000                   0
                   0                   0   0.010000000000000

>> 

2、 stay vs Print the above matrix
2.1 Print Q_ matrix
I am here vs Middle computation HQH’ There was a problem , The code is as follows ：

printf("**********************\n");
				Q_ = mat(nv, nv);
				matmul("TN", nv, NX, NX, 1.0, H_, Q, 0.0, Q);
				matmul("NN", nv, nv, NX, 1.0, Q, H_, 0.0, Q);
				printmat(Q, nv, nv, "Q");

among ,matmul Is a function of matrix multiplication ,T Means transpose ,N Means no transpose ;H_ It's the coefficient matrix , Unweighted coefficient matrix , yes rescode Function returns directly H A copy of the ,Q yes lsq The return value of ,Q_ Express HQH’, Then the print result obtained according to the above code is shown in the following figure ：

Diagonal elements have negative values , And it's not a diagonal matrix , It's obviously wrong , Ha ha ha
2.2、 Print coefficient matrix H
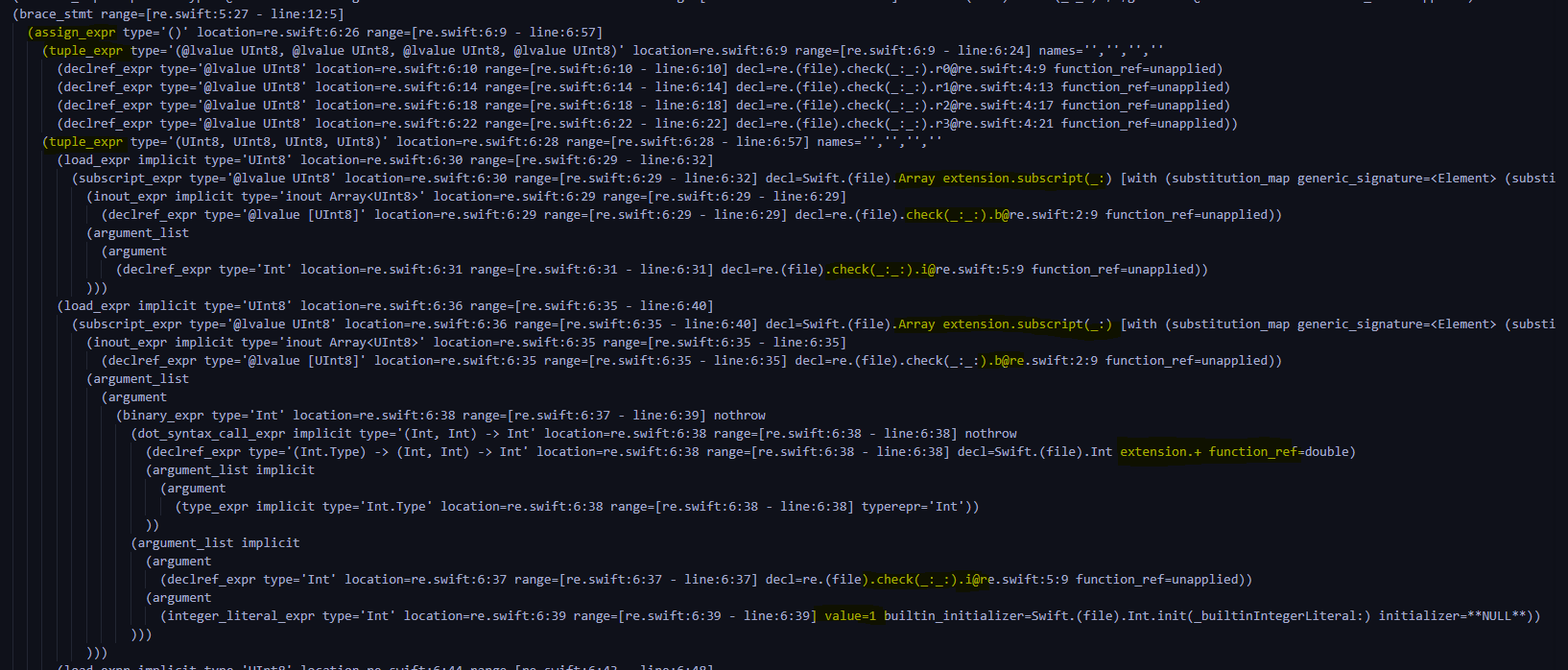
stay rescode Function H Is in accordance with the [-e1 -e2 -e3 1.0 0.0 0.0 0.0] Put in an array or matrix like this , This is the nv * NX An element , I press mat Defined NX * nv To print , Again according to nv * NX To print , give the result as follows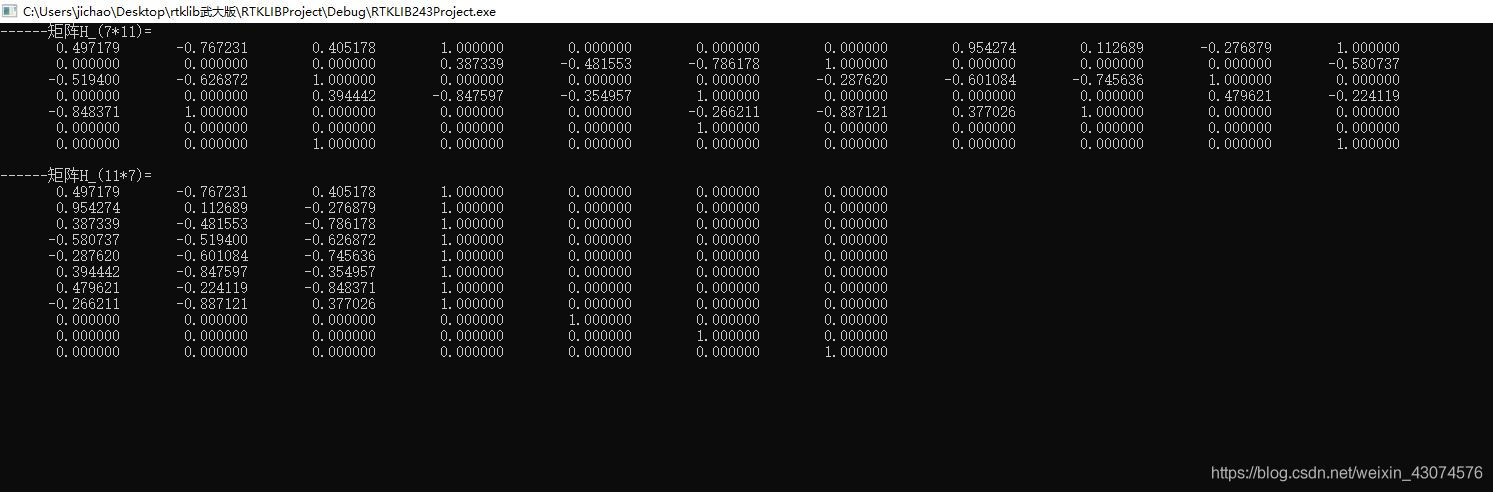

coefficient matrix H be supposed to NX * nv, The printing result shows that the internal data arrangement should be in the form of transposition of the second printing matrix mentioned above , in other words H The form of is actually matlab in H’ In the form of
2.3、 Print H‘ * H
In order to verify 2.2 The above conclusion , That's right H’ * H Print the results of , As shown in the figure below ：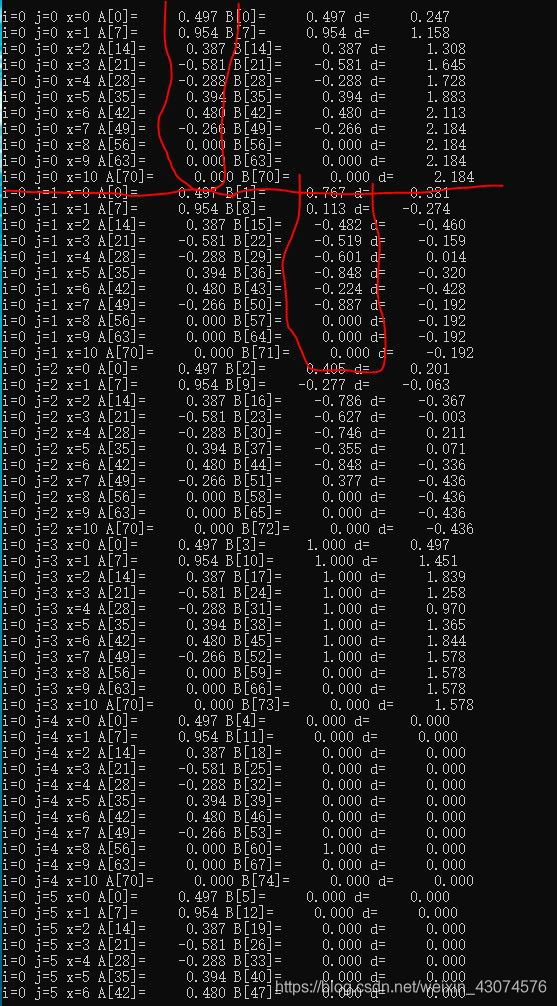

2.4、 Yes 2.1 Modification and verification of matrix multiplication operation in
First pair H Multiply with the identity matrix , Work it out H‘, Proceed again H‘QH operation

				// 3、 According to the law of covariance propagation ,Qvv=Qll-B*Q*B',Q=(B'PB)^-1
				// lsq:  n<m,n=NX m=nv
				//      matmul("NN",n,1,m,1.0,A,y,0.0,Ay); /* Ay=A*y */
				//		matmul("NT", n, n, m, 1.0, A, A, 0.0, Q);  /* Q=A*A' */

				
				printf("**********************\n");
				Q_ = mat(nv, nv);
				double *eyeI;
				double *tH;
				eyeI = mat(NX, NX);
				tH = mat(nv, NX);
				for (j = 0; j < NX;j++)
				{
					for (k = 0; k < NX;k++)
					{
						eyeI[j + k*NX] = (j==k)?1.0:0.0;
					}
				}
				matmul("TN", nv, NX, NX, 1.0, H_, eyeI, 0.0, tH); /*  Find the transpose matrix H' */
				printmat(tH, NX, nv, "tH");//  Print transpose matrix 
				double *Q1,*Q2;
				Q1 = mat(nv, NX);
				Q2 = mat(nv, nv);
				matmul("NN", nv, NX, NX, 1.0, tH, Q, 0.0, Q1);
				matmul("NN", nv, nv, NX, 1.0, Q1, H_, 0.0, Q_);
				printmat(Q_, nv, nv, "Q_"); 

The results are as follows ：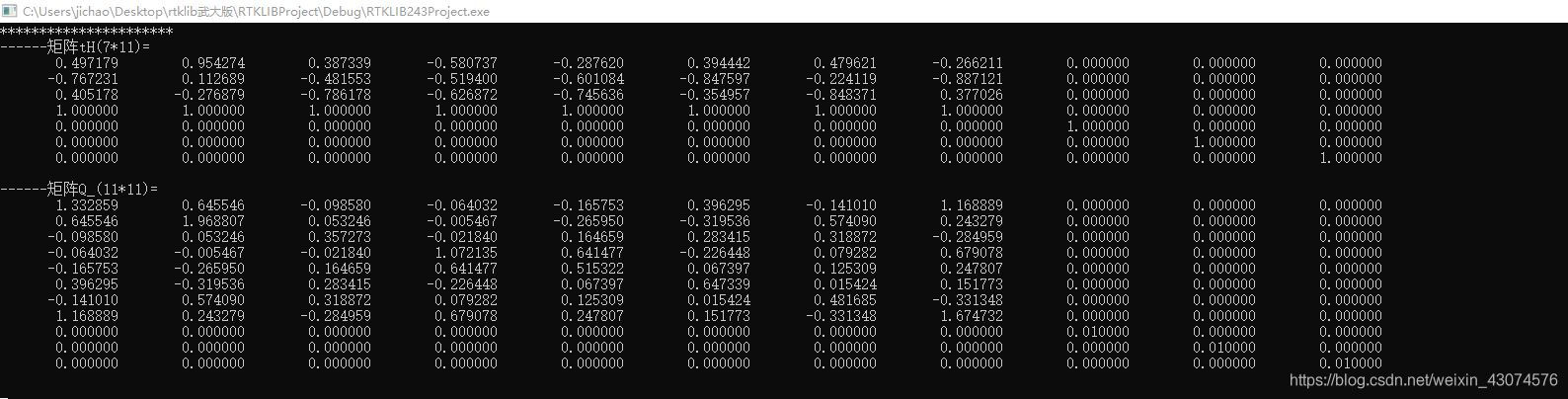

Actually this tH Namely Matlab Medium H Transpose form of , It is verified by debugging again rtklib The matrix of is in the first column 、 Second column ... The first n The form of columns fills the matrix , It's different from our usual habit of writing code by ourselves . Print the results and Matlab It's the same .

Robust code
spp The code that adds robustness to the code is also written , The test verifies , It's really anti poor rms and std It's smaller than the one without resistance , Wait for me to add the comments of the code , Will be able to Test data + Code + Result chart release , Let's talk about it .