当前位置:网站首页>Basic concepts and properties of binary tree
Basic concepts and properties of binary tree
2022-07-07 18:55:00 【Brant_ zero】
Catalog
One 、 Concept and structure of tree
1.2 Important concepts of tree
1.3 The representation of a tree
Two 、 Concept and structure of binary tree
2.1 The concept of binary tree
2.3 Properties of binary trees
One 、 Concept and structure of tree
1.1 The concept of tree
Trees are a kind of nonlinear Data structure of , He is from n(n>=0) A hierarchical set of finite nodes . It is called a tree because its structure is like an upside down tree , namely Root up , And the leaves are down .
- There is one Special nodes , Called the root node , The root node has no precursor node .
- Except for the root node , The rest of the nodes are divided into M(M>0) Disjoint sets T1、T2……Tn, And every set of them Ti(1 <= i <= n) It is also a subtree with a tree structure similar to that of a tree . The root node of each subtree There is only one precursor , There can be 0 One or more successor nodes .
- therefore , Trees are defined recursively .
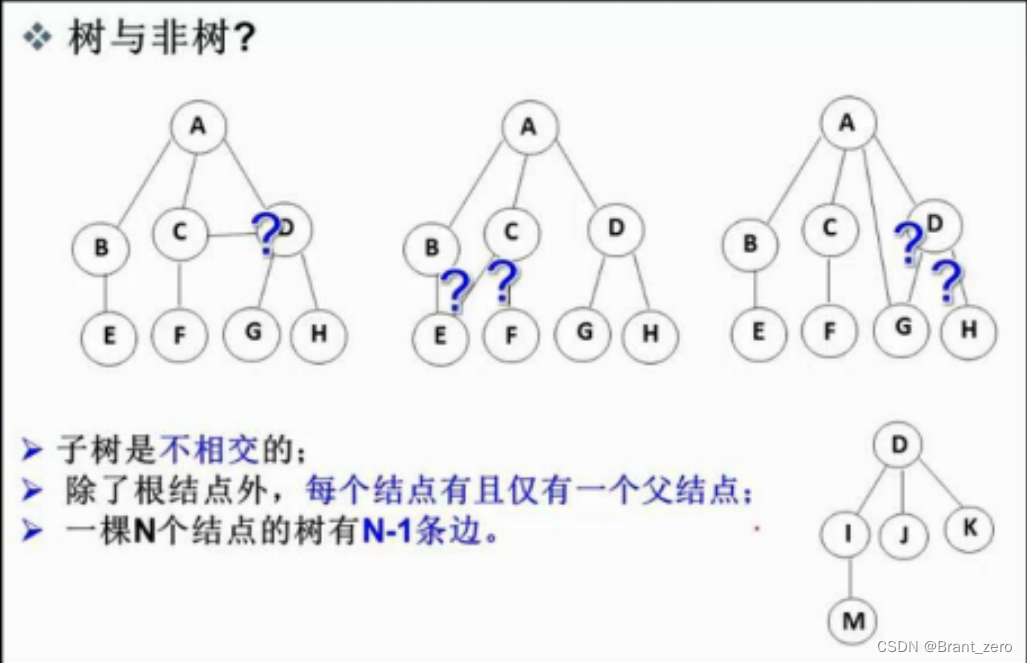
Be careful : In the tree structure , There can be no intersection between subtrees , Otherwise, it is not a tree structure , It should be the data structure of the graph .
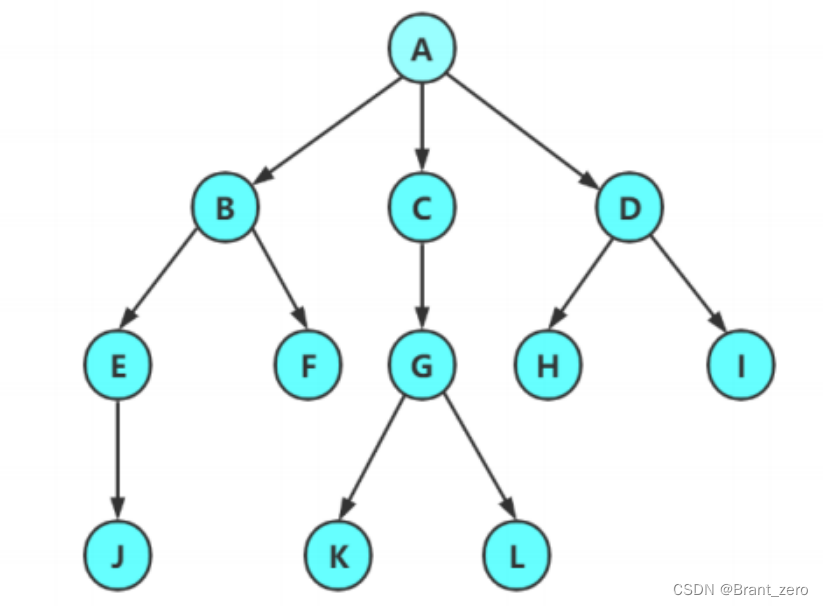
1.2 Important concepts of tree
important :
Degree of node : A node contains Number of subtrees Called the degree of the node ; Pictured above :A The degree of 6.
Leaf node or terminal node : Degree is 0 The node of It's called a leaf node ; Pictured above :B、C、H、I…… Equal as leaf node .
Parent node or parent node : If a node has child nodes , This node is called the parent of its child ; Pictured above :A yes B Parent node .
Child node or child node : The root node of the subtree contained in a node is called the child node of the node ; Pictured above :B yes A The child node of .
The height or depth of a tree : The maximum level of tree node ; Pictured above : The height of the tree is 4.
The ancestor of node : From the root to all nodes on the branch through which the node passes ; Pictured above :A Is the ancestor of all nodes .
descendants : Any node of a subtree rooted from a node is called its descendants . Pictured above : All nodes are A The descendants of .
The degree of a tree : In a tree , The degree of the largest node is called the degree of the tree ; Pictured above : The degree of the tree is 6.
secondly :
Non terminal node or branch node : The degree is not for 0 The node of ; Pictured above :D、E、F、G…… Such nodes are branch nodes .
Brother node : Nodes with the same parent are called siblings ; Pictured above :B、C It's a brother node .
Hierarchy of nodes : Starting from the root , The root is the first layer , The child node of the root is the second layer , And so on ;
Cousin node : The nodes of both parents on the same layer are cousins to each other ; Pictured above :H、I Each other's cousins .
The forest : from m(M>0) A collection of trees that do not intersect each other is called a forest .
1.3 The representation of a tree
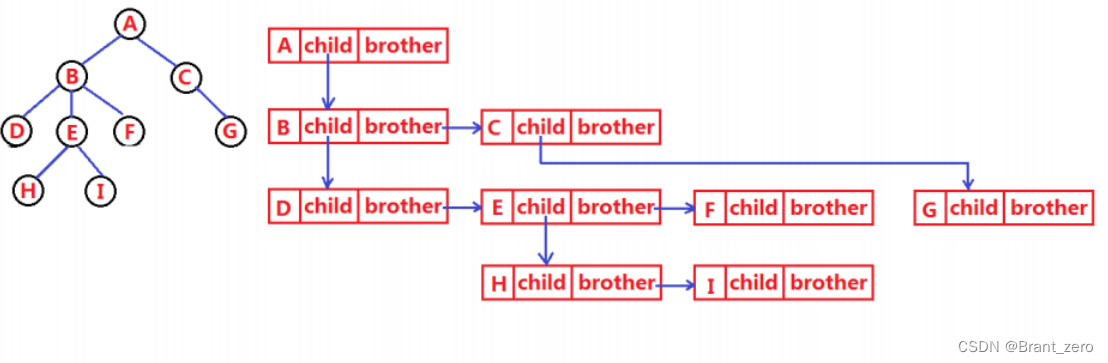
Tree structure is more complex than linear table , Save the value field 、 Also save the relationship between nodes , In practice, there are many ways to represent trees , Here is the most commonly used Child brother notation that will do .
typedef int DataType;
struct Node
{
struct Node* firstChild1; // The first child node
struct Node* pNextBrother; // Point to its next sibling node
DataType data; // Data fields in nodes
};Two 、 Concept and structure of binary tree
2.1 The concept of binary tree
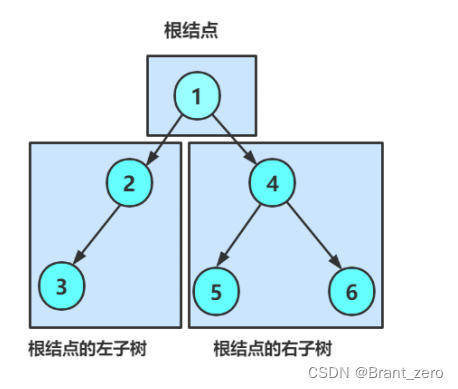
A binary tree is a finite set of nodes , This collection :
- Or empty
- from A root node Add two trees, nicknamed The left subtree and Right subtree The binary tree of .
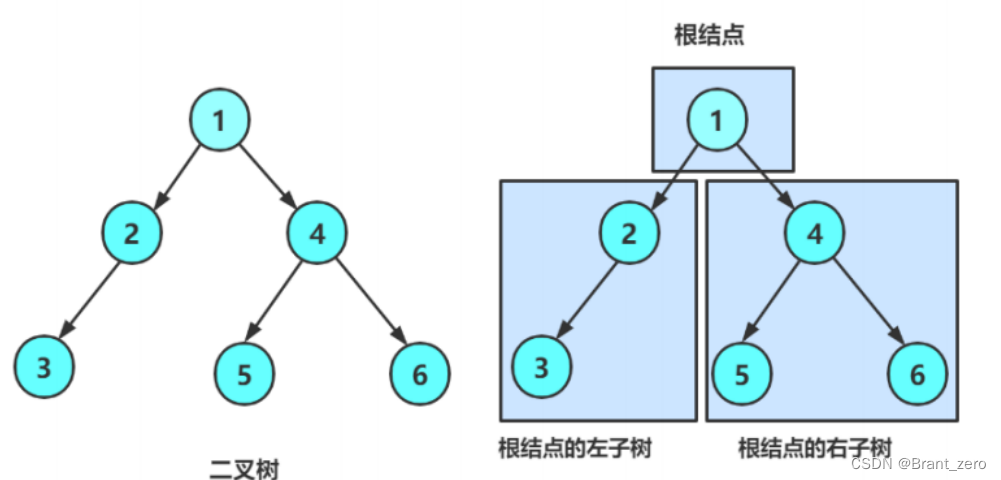
As can be seen from the above figure :
- The degree of nonexistence of binary trees is greater than 2 The node of .
- The subtree of a binary tree has left and right branches , The order cannot be reversed , So a binary tree is an ordered tree .
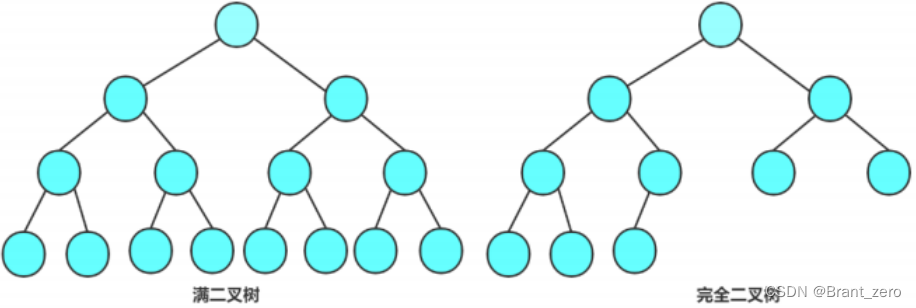
2.2 Special binary tree
- Full binary tree : A binary tree , If the node tree of each layer reaches the maximum , Tut Tut, changing a binary tree is a full binary tree . in other words , If the number of layers of a binary tree is K, And the total number of nodes is
-1, Then it's full of binary trees .
- Perfect binary tree : Complete binary tree is a highly efficient data organization , A complete binary tree is derived from a full binary tree . For a depth of K Of , Yes N A binary tree of nodes , If and only if each of its nodes has a depth of K From the full binary tree of 1 to n The node of —— The corresponding time is called complete binary tree .( The first n The layer is not satisfied, but it is continuous from left to right ,n-1 The floor is full ), It should be noted that a full binary tree is a special kind of complete binary tree .
2.3 Properties of binary trees
important :
- If the specified number of layers of root node is 1, Then the of a non empty binary tree The first i There is a maximum of
Nodes .
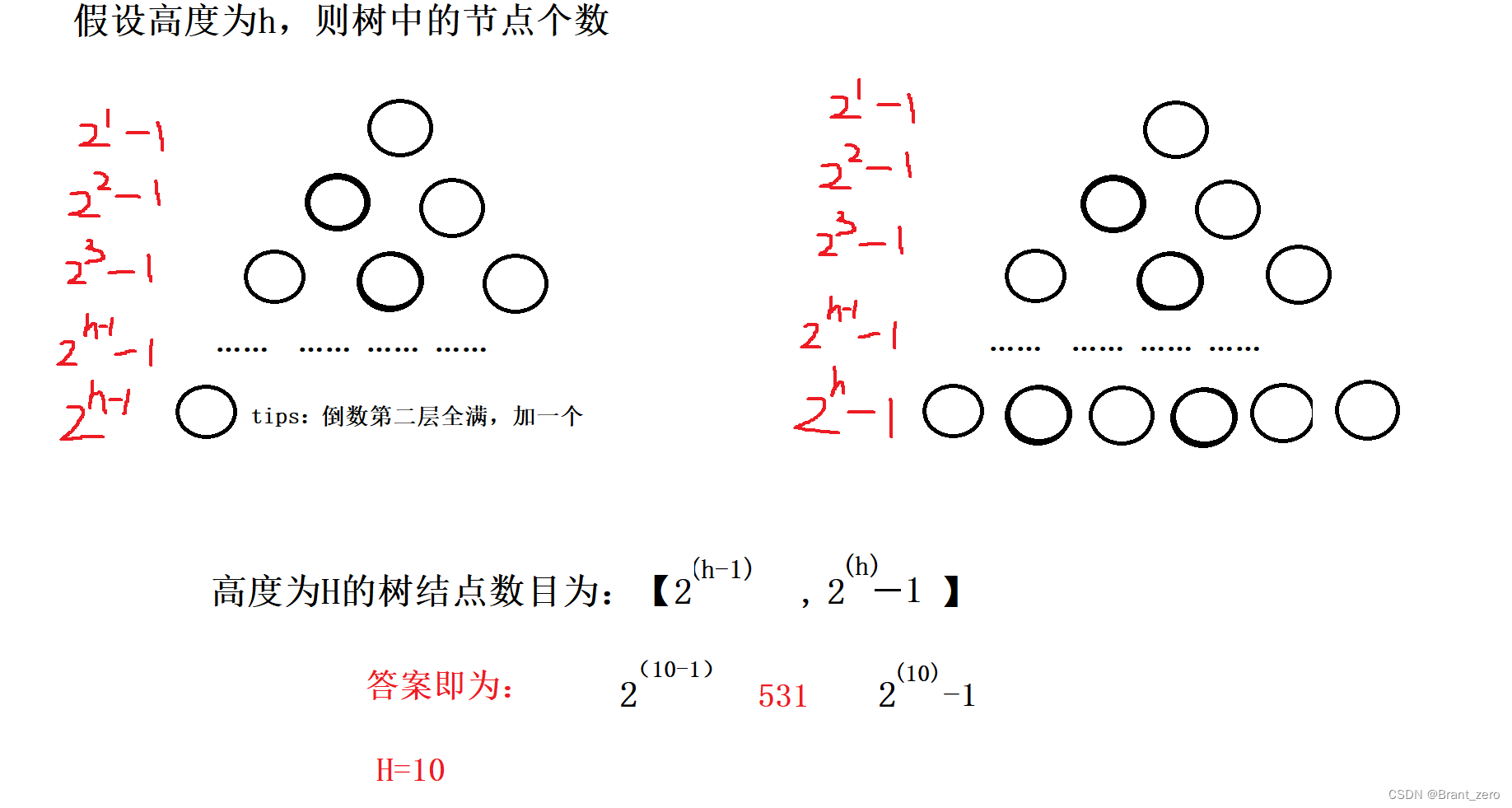
- If the specified number of layers of root node is 1, be Depth is h The largest node of the binary tree of is
.
- For any binary tree , If the degree is 0 The number of leaf nodes is n0,
- If the specified number of layers of the root node is 1, have n The depth of the full binary tree of the node of ,
.
- Those who have n Complete binary tree of nodes , If all nodes are in the array order from top to bottom and from left to right 0 Numbered starting , Then for the serial number is i There are :
- if i>0,i The parent sequence number of the location node :(i-1)/2; i=0, i Number the root node , No parent node
- if 2i+1<n , Left child serial number :2i+1, 2i+1>=n Otherwise no left child
- if 2i+2<n , Right child number :2i+2,2i+2>=n Otherwise no right child
2.4 Binary tree exercise
1. A binary tree has 399 Nodes , Among them is 199 The individual degree is 2 The node of , Then the number of leaf nodes in the binary tree is ()A There is no such binary treeB 200C 198D 199
2. In the following data structure , What is not suitable for sequential storage structure is ()A Incomplete binary treeB Pile upC queueD Stack
3. In possession of 2n In a complete binary tree of nodes , The number of leaf nodes is ()A nB n+1C n-1D n/2
4. The number of nodes in a complete binary tree is 531 individual , Then the height of this tree is ()A 11B 10C 8D 12
5. One has 767 A complete binary tree of nodes , The number of leaf nodes is ()A 383B 384C 385D 386
answer :
The first question is :
The second question is : B
Third question :
Fourth question :
Fifth question :
This concludes this article , The emphasis is on the concept of tree and the properties of binary tree , These are the essence of understanding binary trees , It is also the starting point of the exam , I hope you can understand .
The next blog will bring the basic structure and functions of chain binary tree , I hope you will continue to pay attention .
边栏推荐
- Recommend free online SMS receiving platform in 2022 (domestic and foreign)
- C语言中匿名的最高境界
- 财富证券证券怎么开户?通过链接办理股票开户安全吗
- Continuous test (CT) practical experience sharing
- 线程池中的线程工厂
- [paper sharing] where's crypto?
- 回归问题的评价指标和重要知识点总结
- How to open an account for wealth securities? Is it safe to open a stock account through the link
- 不能忽略的现货白银短线操作小技巧
- Redis的发布与订阅
猜你喜欢
随机推荐
Unlike the relatively short-lived industrial chain of consumer Internet, the industrial chain of industrial Internet is quite long
nest. Database for getting started with JS
RIP和OSPF的区别和配置命令
App capture of charles+drony
来了!GaussDB(for Cassandra)新特性亮相
GSAP animation library
Rules for filling in volunteers for college entrance examination
ip netns 命令(备忘)
不能忽略的现货白银短线操作小技巧
Disk storage chain B-tree and b+ tree
Summary of debian10 system problems
Redis
Ten thousand words nanny level long article -- offline installation guide for datahub of LinkedIn metadata management platform
[principle and technology of network attack and Defense] Chapter 6: Trojan horse
DataSimba推出微信小程序,DataNuza接受全场景考验? | StartDT Hackathon
3.关于cookie
Three forms of multimedia technology commonly used in enterprise exhibition hall design
PTA 1102 教超冠军卷
线程池的拒绝策略
Backup Alibaba cloud instance OSS browser
 -1, Then it's full of binary trees .
-1, Then it's full of binary trees . Nodes .
Nodes . .
. .
.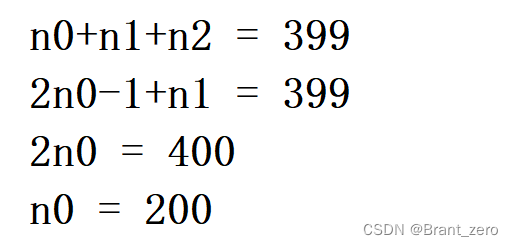
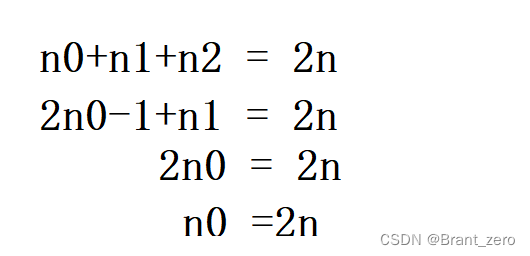
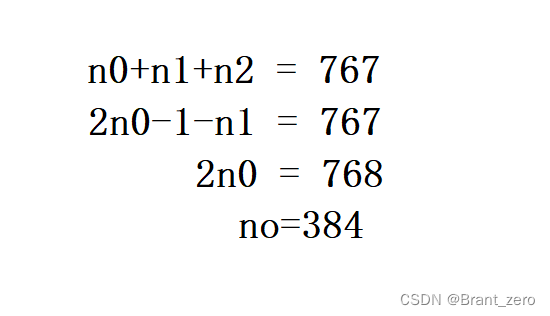




![[论文分享] Where’s Crypto?](/img/27/9b47bfcdff8307e63f2699d6a4e1b4.png)
![[tpm2.0 principle and Application guide] Chapter 5, 7 and 8](/img/38/93fd986916193803bbd90805f832fa.png)