Chapter 5 neural network

1. Try to describe common activation functions , Try to describe the linear function $f(x)=w^{T}x$ Defects used as neuron activation function

1.1 What is an activation function

Here's the picture , Here's the picture , In neurons , Input inputs By weighting , After summing up , A function is also applied , This function is the activation function Activation Function.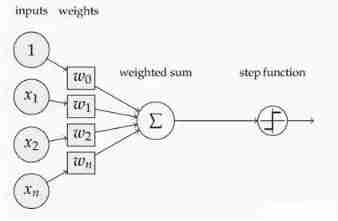

1.2 The function of activation

If you don't use the excitation function , The output of each layer is a linear function of the upper input , No matter how many layers the neural network has , The output is a linear combination of inputs , This is why linear activation functions are not used .
If used , Activation functions introduce nonlinear factors into neurons , So that the neural network can arbitrarily approximate any nonlinear function , So the neural network can be applied to many nonlinear models .

1.3 Common activation functions

• Sigmoid Activation function
  sigmoid Is the most widely used type of activation function , With exponential function shape , It is closest to biological neuron in physical sense . Besides ,$(0,1)$ The output of can also be expressed as probability , Or normalization for input , Typical examples are Sigmoid Cross entropy loss function .
  However ,sigmoid It also has its own shortcomings , The most obvious is saturation . You can see it in the picture below , Its derivatives on both sides gradually approach 0 . Those with this property are called soft saturation activation functions . Concrete , Saturation can be divided into left saturation and right saturation . Corresponding to soft saturation is hard saturation .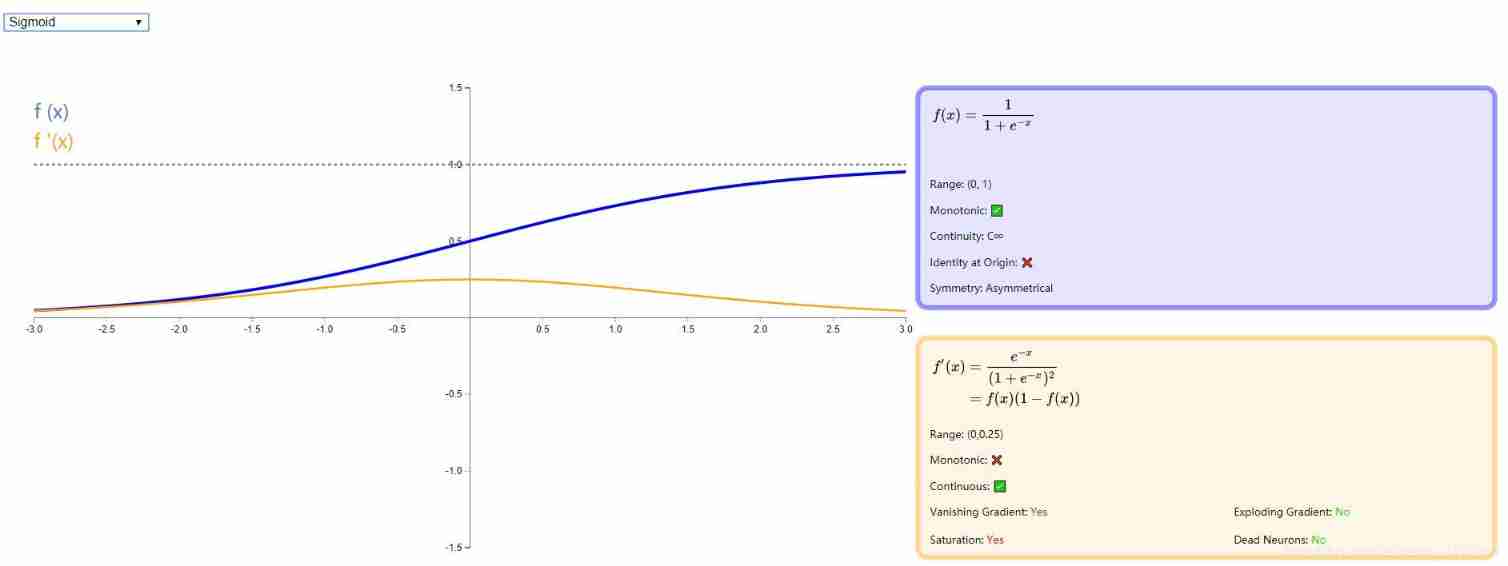
  
• Tanh function
  tanh Is a hyperbolic tangent function ,tanh Functions and sigmod The curve of the function is relatively similar , Let's compare . First of all, the same is , When the input of these two functions is large or small , The output is almost smooth , The gradient is very small , It is not conducive to weight update ; The difference is the output interval ,tanh The output interval of is in (-1,1) Between , And the whole function is based on 0 Centred , This feature is better than sigmod Good. .
  In general binary classification problems , Hidden layer with tanh function , For output layer sigmod function . But these are not invariable , What activation function is used , Or we should analyze it according to specific problems , It still depends on debugging .

See the figure below for details ：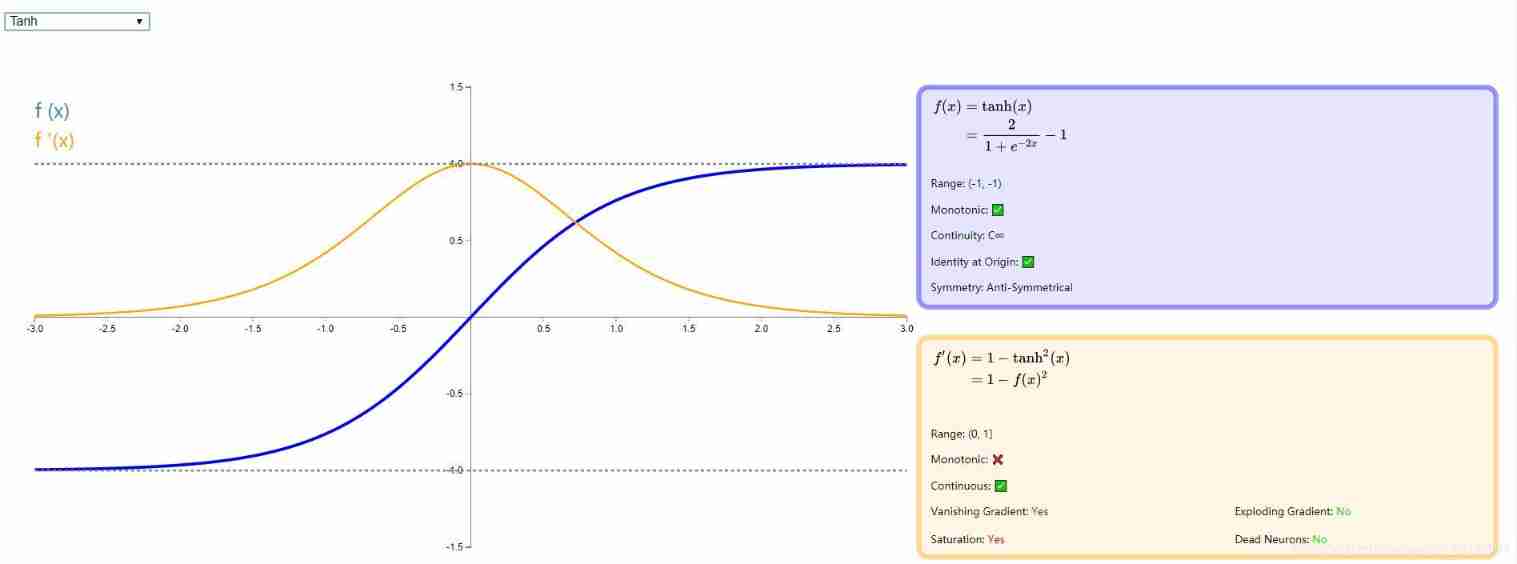

• ReLU
  ReLU The full name is ：Rectified linear unit, It is a popular activation function at present , It retains something similar step That biological neuronal mechanism ： When the input exceeds the threshold, it will fire . Although in 0 Points cannot be derived , However, it does not affect its effective role in gradient based back propagation . of ReLU Detailed introduction , Please move on to the paper ：《Rectified Linear Units Improve Restricted Boltzmann Machines》 There is also a blog with a comprehensive introduction ： Neural network review - Relu Activation function .
  Here is the following ：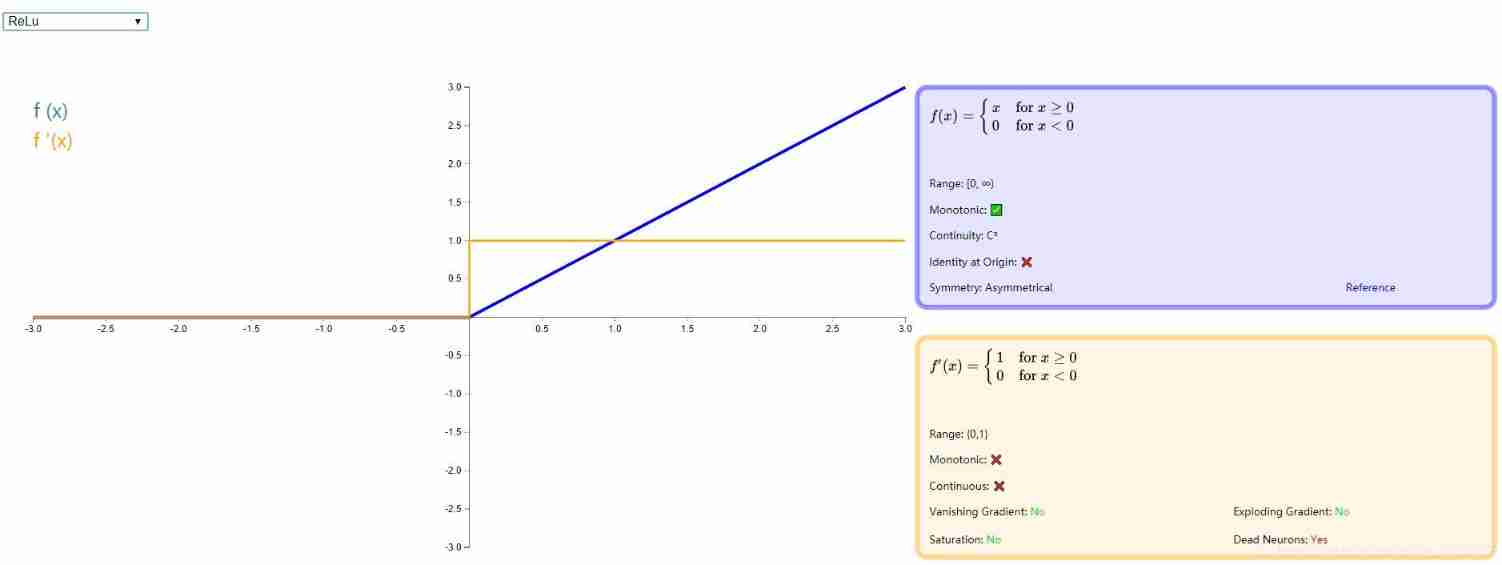
  
• Leaky ReLU
  because ReLU All parts less than zero are classified as 0 , This is very easy to cause Neuron death , therefore Andrew L. Maas Wait for someone in the paper 《Rectifier Nonlinearities Improve Neural Network Acoustic Models》 A new activation function is proposed in , In less than 0 Add a very small slope in the direction of . Here's the picture ：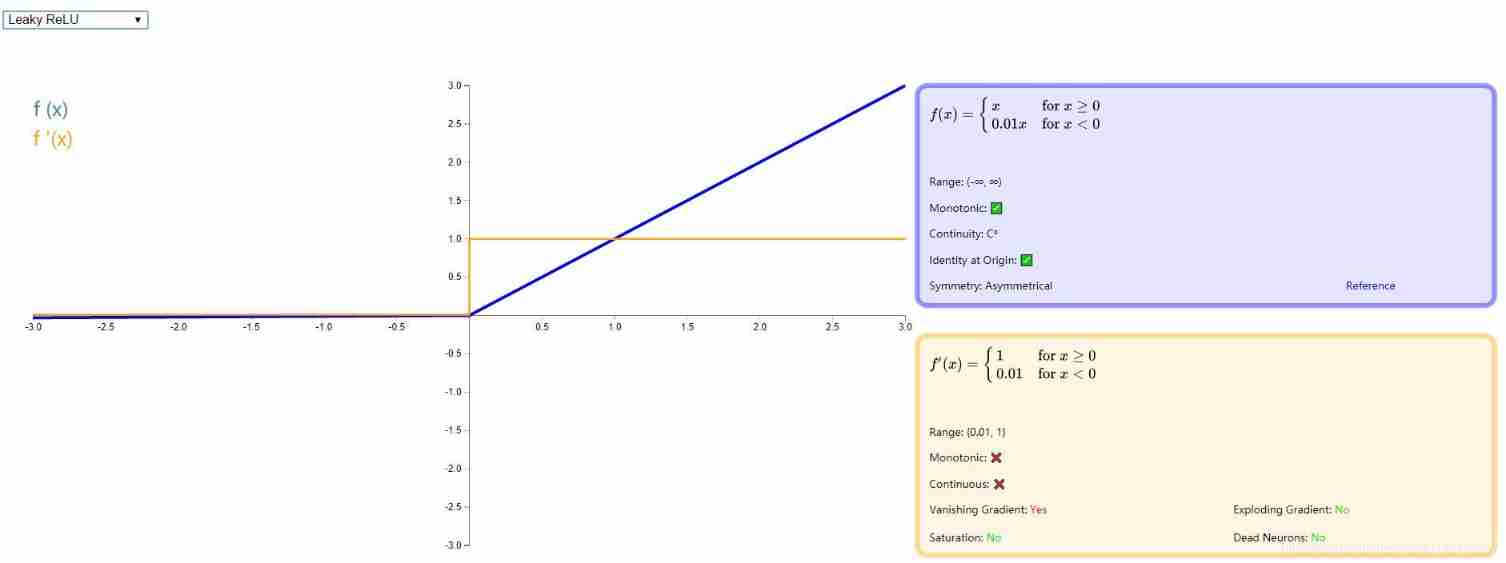
  

2. Perceptrons and multilayer networks

2.1 perceptron

perceptron （Perceptron） It's made up of two layers of neurons , As shown in the figure , The input layer receives the external input signal and passes it to the output layer , The output layer is M−PM−P Neuron , Also known as “ Threshold logical unit ”.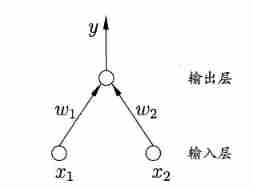

More generally , Given the training data set , The weight $w_i$ And the threshold $\theta$ You can learn . threshold $\theta$ It can be regarded as a fixed input $-1.0$ Of “ Dumb node ” Multiple corresponding connection weights $w_{n+1}$. such , Weight and threshold learning can be unified as weight learning . The learning rules of perceptron are very simple , For training samples $(x,y)$, If the output of the current sensor is $\hat{y}$, Then the weight of the perceptron will be optimally adjusted ：
$$\begin{gathered} w_i\leftarrow w_i+\Delta w_i \\ \Delta w_i=\eta (y-\hat{y})x_i \end{gathered}$$
among $\eta \in (0,1)$ be called “ Learning rate （learing rate）” . It can be seen from the above formula , If the perceptron is on the training sample $(x,y)$ The prediction is correct , Then the perceptron does not change , Otherwise, the weight will be adjusted according to the degree of error . The perceptron has only output layer neurons to process the activation function , That is, only one layer of functional neurons , Their learning ability is very limited . It can only deal with linearly separable cases , Unable to deal with non-linear separable cases .

2.2 Multi layer network

To solve the nonlinear separable problem , We need to consider using multi-layer functional neurons . A layer of neurons between the output layer and the input layer , It is called hidden layer or hidden layer , Hidden layer and output layer neurons are functional neurons with activation function .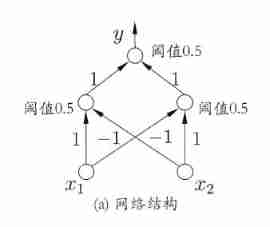

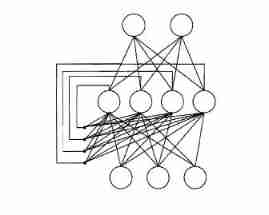
More generally , Common neural networks are shown in the figure below , Each layer of neurons is fully interconnected with the next layer of neurons , There is no same layer connection between neurons , There is no cross layer connection . Such neural network results are usually called “ Multilayer feedforward neural network ”（multi-layer feedforward neural networks）, The input layer neuron receives external input , Hidden layer and output layer neurons process signals , The final result is output by the output layer neurons ; In other words , Input layer neurons only accept input , No function processing , The hidden layer and the output layer contain functional neurons .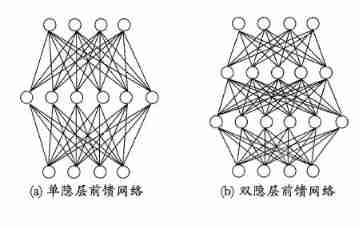

3. Try to use sigmoid The relationship between neurons of activation function and logarithmic probability regression .

Both are related to $sigmoid$ Function related , But in logarithmic probability regression ,$sigmoid$ The function is to convert the predicted value generated by the linear regression model （ It's worth it ） Turn into $0/1$ value . $sigmoid$ Function is used to replace unit step function , because $sigmoid$ The function is monotonic and differentiable ; In the neuron model , $sigmoid$ Function as “ Activation function ” Used to process the output of neurons , Because neurons in the neuron model receive signals from $n$ The input signals from these other neurons , These input signals are transmitted through weighted connections , The total input received by the neuron is compared with the threshold of the neuron , use “ Activation function ” It can convert the output value into $0/1$ value .

3. For Graphs 5.7（102 page ） Medium , Try to deduce BP Update formula in the algorithm

For training example $({\mathbf{x}}_k,{\mathbf{y}}_k)$, Suppose the output of the neural network is ${\hat{y}}_k=({\hat{y}}_1^k,{\hat{y}}_2^k,...,{\hat{y}}_l^k)$, namely ${\hat{y}}_j^k=f({\beta }_j-{\theta }_j)$ ,
Then the network is $({\mathbf{x}}_k,{\mathbf{y}}_k)$ The mean square error of is ：
$$E_k=\frac{1}{2}\sum _{j=1}^l({\hat{y}}_j^k-{\hat{y}}_j^k{)}^2$$
Arbitrary parameters $v$ The updated estimation formula is $$v\leftarrow v+\Delta v$$
For errors $E_k$, Given the learning rate $\eta$, Yes $$\Delta w_{hj}=-\eta \frac{\partial E_k}{\partial w_{hj}}.$$
Can be derived ：
$$\begin{gathered} \frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial {\hat{y}}_j^k}.\frac{\partial {\hat{y}}_j^k}{\partial {\beta }_j}.\frac{\partial {\beta }_j}{\partial w_{hj}}. \\ \frac{\partial {\beta }_j}{\partial w_{hj}}=b_h \\ {f}^{\prime }(x)=f(x)(1-f(x)) \\ {g}_j=-\frac{\partial E_k}{\partial {\hat{y}}_j^k}.\frac{\partial {\hat{y}}_j^k}{\partial {\beta }_j} \\ =-({\hat{y}}_j^k-y_j^k)f^{\prime }({\beta }_j-{\theta }_j) \\ ={\hat{y}}_j^k(1-{\hat{y}}_j^k)(y_j^k-{\hat{y}}_j^k) \end{gathered}$$
And then you get it BP The algorithm is about $w_{hj}$ The updated formula of $$\Delta w_{hj}=\eta g_j{b}_h.$$
Similar can be obtained $$\begin{gathered} \Delta {\theta }_j=-\eta g_j, \\ \Delta v_{ih}=\eta e_h{x}_i, \\ \Delta \gamma =-\eta e_h, \end{gathered}$$
among $$\begin{gathered} e_h=\frac{\partial E_k}{\partial b_h}.\frac{\partial b_h}{\partial {\alpha }_h} \\ =-\sum _{j=1}^l\frac{\partial E_k}{\partial {\beta }_j}.\frac{\partial {\beta }_j}{\partial b_h}{f}^{\prime }({\alpha }_h-{\gamma }_h) \\ =\sum _{j=1}^l{w}_{hj}{g}_j{f}^{\prime }({\alpha }_h-{\gamma }_h) \\ =b_h(1-b_h)\sum _{j=1}^l{w}_{hj}{g}_j \end{gathered}$$

4. Try to describe the standard BP Algorithm and accumulation BP Algorithm , Try programming to realize the standard BP Algorithm and accumulation BP Algorithm , Using these two algorithms to train a single hidden layer neural network on watermelon data set , And compare

Here's the thing , BP The goal of the algorithm is to minimize the training set $D$ Cumulative error on
$$E=\frac{1}{m}\sum _{k=1}^m{E}_k$$ But what we introduced above " standard BP Algorithm " Update the connection weights and thresholds for only one training sample at a time , in other words , The update rules of the algorithm are based on a single $E_k$ Derived from . As a result, an update rule based on the minimization of cumulative error is similarly derived , The cumulative error inverse propagation is obtained (accumulated error backpropagation) Algorithm . The cumulative BP Algorithms and standards BP Algorithms are commonly used . Generally speaking , standard BP Each update of the algorithm is only for a single sample , Parameters are updated very frequently , Moreover, the effect of updating different samples may appear " offset " The phenomenon . therefore , In order to achieve the same cumulative error minimum , standard BP Algorithms often need more iterations . The cumulative BP The algorithm directly aims at minimizing the cumulative error , It's reading the entire training set $D$ Update parameters after one pass , The frequency of parameter update is much lower . But in many tasks , After the cumulative error decreases to a certain extent , Further decline will be very slow , Standard at this time BP Better solutions tend to be obtained faster , Especially in the training set $D$ It is more obvious when it is very large .

5. Try to describe how to alleviate BP Over fitting phenomenon of neural network

because BP（BackPropagation） Neural network has strong representation ability ,PB Neural networks often encounter fitting , The training error continues to decrease , But test errors can go up . There are two strategies commonly used to alleviate BP Overfitting of networks ：

• The first strategy is “ Stop early ”（early stopping）: Divide the data into training set and verification set , The training set is used to calculate the gradient 、 Update connection rights and thresholds , The verification set is used to estimate the error , If the training set error decreases but the verification set error increases , Then stop training , At the same time, the connection weight and threshold with the minimum verification set error are returned .
• The second strategy is “ Regularization ”（regularization）, The basic idea is to add a part to the error objective function to describe the network complexity , For example, the sum of the squares of the connection weight and the threshold .

6. Try to explain RBF The Internet ,RNN Concept and characteristics of recurrent neural network

• RBF It is a single hidden layer feedforward neural network , It uses the radial basis function as the activation function of hidden layer neurons , The output layer is a linear combination of the outputs of neurons in the hidden layer , Suppose the input is $d$ Dimension vector $\mathbf{x}$, Output as real value , be RBF Can be expressed as
  $$\phi (\mathbf{x})=\sum _{i=1}^q\rho (\mathbf{x},{\mathbf{c}}_i)$$
  among $q$ Is the number of neurons in the hidden layer ,$c_{i}and{w}_i$ They are the first $i$ The center and weight of each hidden layer neuron ,$\rho (x,c_i)$ Is the radial basis function , This is a function of radial symmetry , Usually defined as a sample $x$ To the data center $c_i$ A monotonic function of the Euclidean distance between . Common Gaussian radial basis functions are shaped like ：
  $$\rho (x,c_i)=e^{-{\beta }_i||x-c_i|{|}^2}$$ With enough hidden neurons RBF Neural network can approximate any continuous function with any accuracy .

• RNN Cyclic neural network , Different from feedforward neural network ,“ Recursive neural network ”（Recurrent Neural Networks） Allow the network to have a ring structure , The output of some neurons can be fed back as input signals , That is, the network is $t$ The output state of the time is not only related to the input , And also $t-1$ The network state at the moment , Thus, it can deal with the dynamic changes related to time .Elman Network is one of the most commonly used recurrent neural networks , Its structure is similar to multilayer feedforward network , But the output of hidden layer neurons is fed back , Together with the signal provided by the input layer neuron at the next moment , As the input of hidden layer neurons at the next moment . Hidden layer neurons usually adopt $Sigmoid$ Activation function , And network training is often promoted BP Algorithm .
  

7. Try to describe the convolution of convolution neural network 、 Down sampling （ Pooling ） The process , Try to describe the architecture of convolutional neural network

From a computer point of view , The image is actually a two-dimensional matrix , The work of convolution neural network is to use convolution 、 Operations such as pooling extract features from two-dimensional arrays , And recognize the image . In theory , As long as it is data that can be converted into a two-dimensional matrix , Convolutional neural network can be used to identify and detect . For example, sound files , It can be divided into very short segments , The height of each scale can be converted into numbers , In this way, the whole sound file can be converted into a two-dimensional matrix , Similar to text data in natural language , Chemical data in medical experiments and so on , Convolutional neural network can be used to realize recognition and detection .

• Convolution ： Convolution is the core concept of convolutional neural network , It is also the origin of its name . Convolution is used to extract local features of an image , It is a mathematical calculation method , The following figure vividly shows the convolution process .
  

• Pooling
  Pool English is pooling, Another name is down sampling（ Down sampling ）, I have to say that the translation of these two terms is very faithful to the original meaning , But this kind of straightforward translation is very difficult to understand . Use popular language to describe ： Pooling is to divide the characteristic matrix into several small blocks , Select a value from each sub matrix to replace the sub matrix , The purpose of this is to compress the characteristic matrix , Simplify the next calculation . There are two ways to pool ：Max Pooling（ Maximum pooling ） and Average Pooling（ Average pooling ）, The former is to take the maximum value from the submatrix , The latter is to take the average .
  
  Pooling is easier to understand than convolution , The dynamic diagram above simulates a simple pooling process , The Yellow characteristic matrix is divided into four sub matrices , Then select a value from each sub matrix according to the pooling method to form the pooling matrix . Maximum pooling is a commonly used pooling method , Because selecting the maximum value of the region can well maintain the characteristics of the original image .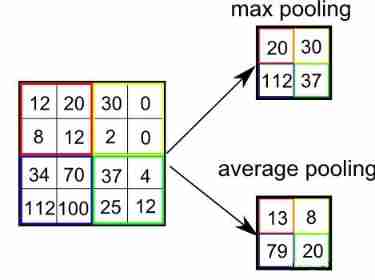
  

• Convolutional neural network architecture
  Here is a common convolutional neural network CNN Basic architecture , As shown in the figure , Network input is a $32\times 32$ The handwritten digital image of , The output is its recognition result ,CNN Compound multiple “ Convolution layer ” and “ Sampling layer ” Process the input signal . Then the mapping between the connection layer and the output target . Each convolution layer contains multiple feature maps , Each feature map is composed of multiple neurons “ Plane ”, A feature of the input is extracted by a convolution filter .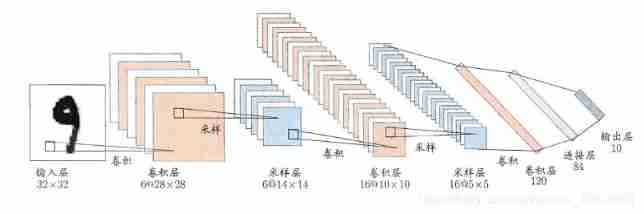
  

8. kaggle Introduction to the game - Handwritten digit recognition , Download data and code , Read the code carefully and mark the code comments in detail .

Reference data ：
https://www.kaggle.com/c/digit-recognizer/overview
Reference code ：
https://www.kaggle.com/elcaiseri/mnist-simple-cnn-keras-accuracy-0-99-top-1