LeetCode：124. Maximum path sum in binary tree

route It is defined as a path starting from any node in the tree , Along the parent node - Child node connection , A sequence that reaches any node . The same node in a path sequence At most once . This path At least one node , And it doesn't have to go through the root node .

Path and Is the sum of the values of the nodes in the path .

Give you the root node of a binary tree root , Back to its The maximum path and .

Example 1：

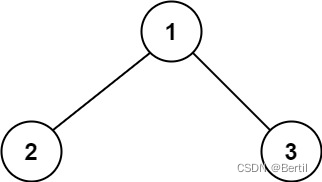
 Input ：root = [1,2,3]
 Output ：6
 explain ： The best path is  2 -> 1 -> 3 , Path and are  2 + 1 + 3 = 6

Example 2：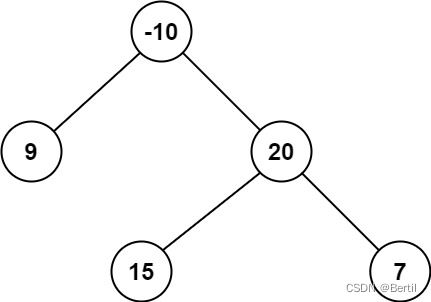

 Input ：root = [-10,9,20,null,null,15,7]
 Output ：42
 explain ： The best path is  15 -> 20 -> 7 , Path and are  15 + 20 + 7 = 42

Tips ：

• The range of nodes in the tree is [1, 3 * 10^4]
• -1000 <= Node.val <= 1000

---

Their thinking

1. First, traverse the depth of the left and right subtrees , The maximum value of the current node can be divided into three cases ：

• Go to the left ： Current node +L( The maximum depth of the left subtree )
• Go to the right ： Current node +R（ The maximum depth of the right subtree ）
• Don't go ： If the current node is negative , Go straight back to 0
  2. Then define the maximum path and ans Root node + The left subtree + Maximum depth of right subtree
  3. Last , After recursion, return the maximum path and ans that will do

Code

/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */
/** * @param {TreeNode} root * @return {number} */
var maxPathSum = function(root) {
    
    let ans = -9999; 
    dfs(root);
    return ans;
    //  Go down from the current node 
    function dfs(root) {
    
        if(!root) return 0;
        //  Traversing the depth of the left subtree 
        let left = dfs(root.left);
        //  Traverse the depth of the right subtree 
        let right = dfs(root.right);
        //  The maximum value of the update path 
        ans = Math.max(ans, root.val + left + right);
        //  Return the maximum value from the current node 
        return Math.max(0, Math.max(left, right) + root.val);
    }
};