当前位置:网站首页>《統計學》第八版賈俊平第七章知識點總結及課後習題答案
《統計學》第八版賈俊平第七章知識點總結及課後習題答案
2022-07-06 14:26:00 【無二三事】
一.考點歸納

參數估計的基本原理
1置信區間
(1)置信水平為95%的置信區間的含義:用某種方法構造的所有區間中有95%的區間包含總體參數的真值。(2)置信度愈高(即估計的可靠性愈高),則置信區間相應也愈寬(即估計准確性愈低)。
(3)置信區間的特點:置信區間受樣本影響,具有隨機性,總體參數的真值是固定的。一個特定的置信區間“總是包含”或“絕對不包含”參數的真值,不存在“以多大的概率包含總體參數”的問題。
2評價估計量的標准
(1)無偏性:估計量抽樣分布的期望值等於被估計的總體參數,即E(θ)=θ。
(2)有效性:估計量的方差盡可能小。
(3)一致性:隨著樣本量的增大,估計量的值越來越接近被估計總體的參數。
一個總體參數的區間估計


二、課後習題及答案
1利用下面的信息,構建總體均值的置信區間。
(1)總體服從正態分布,且已知σ=500,n=15,x=8900,置信水平為95%。
(2)總體不服從正態分布,且已知σ=500,n=35,x=8900,置信水平為95%。
(3)總體不服從正態分布,σ未知,n=35,x=8900,s=500,置信水平為90%。
(4)總體不服從正態分布,σ未知,n=35,x=8900,s=500,置信水平為99%。
解:(1)由於總體服從正態分布,σ=500,n=15,x=8900,α=0.05,z0.05/2=1.96。所以總體均值μ的95%的置信區間為:
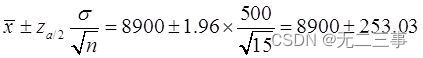
即(8646.97,9153.03)。
(2)已知總體不服從正態分布,但n=35為大樣本,因此采用z統計量,總體均值μ的95%的置信區間為:
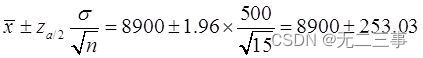
即(8734.35,9065.65)。
(3)已知總體不服從正態分布,σ未知,但由於n=35為大樣本,因此可以采用z統計量,總體均值μ的90%的置信區間為:
即(8760.97,9039.03)。
(4)已知總體不服從正態分布,σ未知,但由於n=35為大樣本,因此可以采用z統計量,總體均值μ的99%的置信區間為:
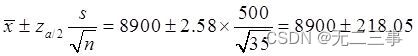
即(8681.95,9118.05)。
2某大學為了解學生每天上網的時間,在全校7500名學生中采取重複抽樣方法隨機抽取36人,調查他們每天上網的時間,得到錶7-3的數據(單比特:小時)。
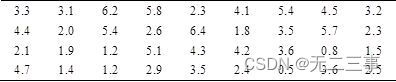
求該校大學生平均上網時間的置信區間,置信水平分別為90%,95%和99%。
解:已知:n=36,當α為0.1,0.05,0.01時,相應的z值分別為:z0.1/2=1.645,z0.05/2=1.96,z0.01/2=2.58
根據樣本數據計算得:
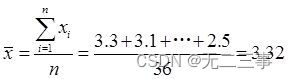
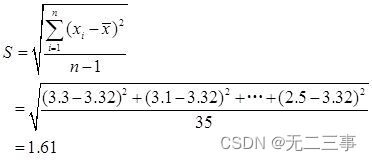
(1)由於n=36為大樣本,所以平均上網時間的90%的置信區間為:
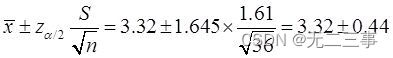
即(2.88,3.76)。
(2)平均上網時間的95%的置信區間為:
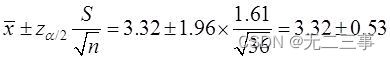
即(2.79,3.85)。
(3)平均上網時間的99%的置信區間為:
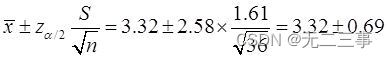
即(2.63,4.01)。
3某企業生產的袋裝食品采用自動打包機包裝,每袋標准重量為100g,現從某天生產的一批產品中按重複抽樣隨機抽取50包進行檢查,測得每包重量如錶所示。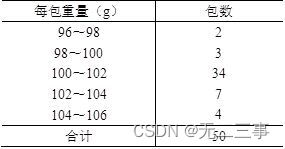
已知食品包重量從正態分布,要求:
(1)確定該種食品平均重量的95%的置信區間。
(2)如果規定食品重量低於100g屬於不合格,確定該批食品合格率的95%的置信區間。
解:(1)已知:總體服從正態分布,但σ未知,n=50為大樣本,α=0.05,z0.05/2=1.96。根據分組的樣本數據計算得:x=(97×2+99×3+…+105×4)/50=101.32
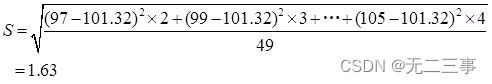
該種食品平均重量的95%的置信區間為:
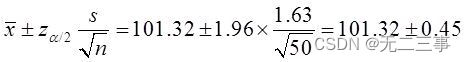
即(100.87,101.77)。
(2)根據樣本數據可知,樣本合格率為p=45/50=0.9。該種食品合格率的95%的置信區間為:
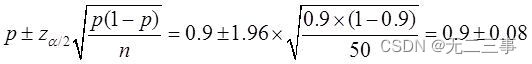
即(0.82,0.98)。
4假設總體服從正態分布,利用錶7-5的數據構建總體均值μ的99%的置信區間。

解:已知:總體服從正態分布,但σ未知,n=25為小樣本,α=0.01,t0.01/2(25-1)=2.797。根據樣本數據計算得:x=16.128,s=0.871。則總體均值μ的99%的置信區間為:
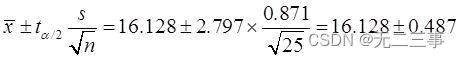
即(15.64,16.62)。
5利用下面的樣本數據構建總體比例π的置信區間。
(1)n=44,p=0.51,置信水平為99%。
(2)n=300,p=0.82,置信水平為95%。
(3)n=1150,p=0.48,置信水平為90%。
解:(1)已知:n=44,p=0.51,α=0.01,z0.01/2=2.58。總體比例π的99%的置信區間為:
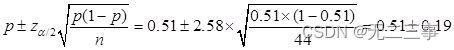
即(0.32,0.70)。
(2)已知:n=300,p=0.82,α=0.05,z0.05/2=1.96。總體比例π的95%的置信區間為:
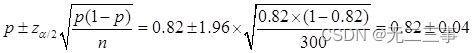
即(0.78,0.86)。
(3)已知:n=1150,p=0.48,α=0.1,z0.1/2=1.645。總體比例π的90%的置信區間為:
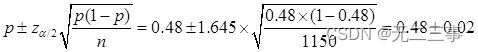
即(0.46,0.50)。
6在一項家電市場調查中,隨機抽取了200個居民戶,調查他們是否擁有某一品牌的電視機。其中擁有該品牌電視機的家庭占23%。求總體比例的置信區間,置信水平分別為90%和95%。解:已知:n=200,p=0.23,α為0.1和0.05時,相應的z0.1/2=1.645,z0.05/2=1.96。
(1)總體比例π的90%的置信區間為:
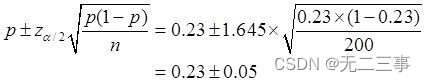
即(0.18,0.28)。
(2)總體比例π的95%的置信區間為:
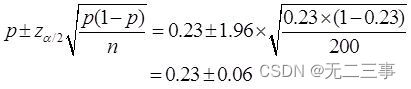
即(0.17,0.29)。
7一比特銀行的管理人員想估計每比特顧客在該銀行的月平均存款額。他假設所有顧客月存款額的標准差為1000元,要求的估計誤差在200元以內。置信水平為99%,應選取多大的樣本?解:已知:σ=1000,估計誤差E=200,α=0.01,z0.01/2=2.58。所以應抽取的樣本量為:
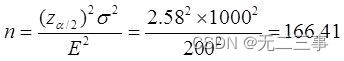
所以應抽取167個樣本。
8某居民小區共有居民500戶,小區管理者准備采用一種新的供水設施,想了解居民是否贊成。采取重複抽樣方法隨機抽取了50戶,其中有32戶贊成,18戶反對。
(1)求總體中贊成該項改革的戶數比例的置信區間(α=0.05)。
(2)如果小區管理者預計贊成的比例能達到80%,估計誤差不超過10%。應抽取多少戶進行調查(α=0.05)?
解:(1)已知:n=50,p=32/50=0.64,α=0.05,z0.05/2=1.96。總體中贊成該項改革的戶數比例的95%的置信區間為:
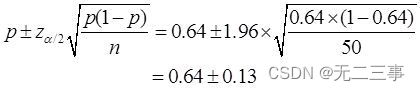
即(0.51,0.77)。
(2)已知:π=0.80,α=0.05,z0.05/2=1.96。應抽取的樣本量為:
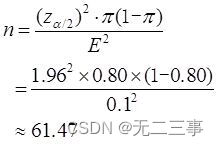
即應抽取的樣本量為62戶。
9根據下面的樣本結果,計算總體標准差σ的90%的置信區間。
(1)x=21,s=2,n=50。
(2)x=1.3,s=0.02,n=15。
(3)x=167,s=31,n=22。
解:(1)已知:x=21,s=2,n=50,α=0.1,查錶得:χ20.1/2(50-1)=66.3387,χ21-0.1/2(50-1)=33.9303。總體方差σ2的置信區間為:
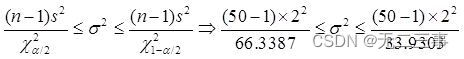
即2.95≤σ2≤5.78。標准差的置信區間為:1.72≤σ≤2.40。
(2)已知:x=1.3,s=0.02,n=15,α=0.1,查錶得:χ20.1/2(15-1)=23.6848,χ21-0.1/2(15-1)=6.5706。總體方差σ2的置信區間為:
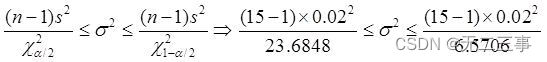
標准差的置信區間為:0.015≤σ≤0.029。
(3)已知:x=167,s=31,n=22,α=0.1,查錶得:χ20.1/2(22-1)=32.6706,χ21-0.1/2(22-1)=11.5913。總體方差σ2的置信區間為:
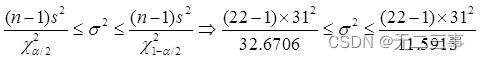
標准差的置信區間為:24.85≤σ≤41.73。
10顧客到銀行辦理業務時往往需要等待一段時間,而等待時間的長短與許多因素有關。比如,銀行業務員辦理業務的速度,顧客等待排隊的方式等。為此,某銀行准備采取兩種排隊方式進行試驗,第一種排隊方式是:所有顧客都進入一個等待隊列;第二種排隊方式是:顧客在三個業務窗口處列隊三排等待。為比較哪種排隊方式使顧客等待的時間更短,銀行各隨機抽取10名顧客,他們在辦理業務時所等待的時間(單比特:分鐘),如錶所示。![]()
要求:
(1)構建第一種排隊方式等待時間標准差的95%的置信區間。
(2)構建第二種排隊方式等待時間標准差的95%的置信區間。
(3)根據(1)和(2)的結果,你認為哪種排隊方式更好?
解:(1)已知:n=10,α=0.05,查錶得χ0.05/22(10-1)=19.0228,χ1-0.05/22(10-1)=2.7004。根據方式1的樣本數據計算得:s2=0.2272。總體方差σ2的置信區間為:
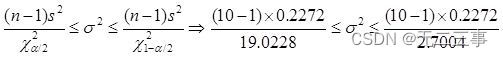
標准差的置信區間為:0.33≤σ≤0.87。
(2)根據方式2的樣本數據計算得:s2=3.3183。總體方差σ2的置信區間為:
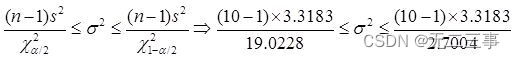
標准差的置信區間為:1.25≤σ≤3.33。
(3)第一種排隊方式更好,因為它的離散程度小於第二種排隊方式。
11從兩個正態總體中分別抽取兩個獨立的隨機樣本,它們的均值和標准差如錶所示。
(1)設n1=n2=100,求(μ1-μ2)95%的置信區間。
(2)設n1=n2=10,σ12=σ22,求(μ1-μ2)95%的置信區間。
(3)設n1=n2=10,σ12≠σ22,求(μ1-μ2)95%的置信區間。
(4)設n1=10,n2=20,σ12=σ22,求(μ1-μ2)95%的置信區間。
(5)設n1=10,n2=20,σ12≠σ22,求(μ1-μ2)95%的置信區間。
解:(1)由於兩個樣本均為獨立大樣本,σ12和σ22未知。當α=0.05時,z0.05/2=1.96,則μ1-μ2的95%的置信區間為:
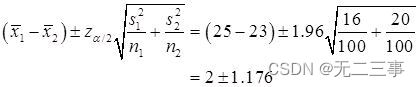
即(0.824,3.176)。
(2)由於兩個樣本均為來自正態總體的獨立小樣本,當σ12和σ22未知但σ12=σ22時,需要用兩個樣本的方差s12和s22和來估計。總體方差的合並估計量sp2為:

當α=0.05時,t0.05/2(10+10-2)=2.101,則μ1-μ2的95%的置信區間為:
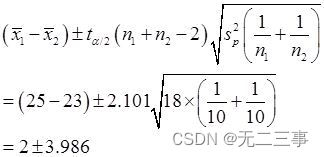
即(-1.986,5.986)。
(3)由於兩個樣本均為來自正態總體的獨立小樣本,σ12和σ22未知且σ12≠σ22,n1=n2=n。當α=0.05時,t0.05/2(10+10-2)=2.101,則μ1-μ2的95%的置信區間為:

即(-1.986,5.986)。
(4)由於兩個樣本均為來自正態總體的獨立小樣本,σ12和σ22未知但σ12=σ22,n1≠n2。需要用兩個樣本的方差s12和s22來估計。總體方差的合並估計量sp2為:
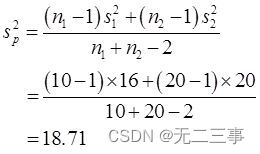
當α=0.05時,t0.05/2(10+20-2)=2.048。因此,μ1-μ2的95%的置信區間為:
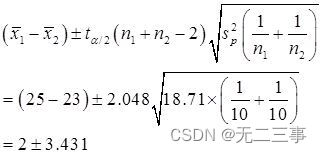
即(-1.431,5.431)。
(5)由於兩個樣本均為來自正態總體的獨立小樣本,σ12和σ22未知且σ12≠σ22,n1≠n2。因此,μ1-μ2的95%的置信區間為:
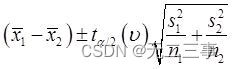
自由度的計算如下:
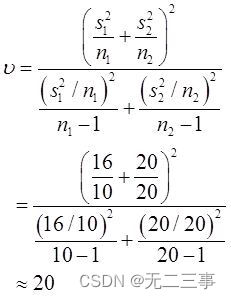
當α=0.05時,t0.05/2(20)=2.086。μ1-μ2的95%的置信區間為:
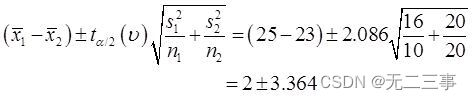
即(—1.364,5.364)。
12錶7-8是由4對觀察值組成的隨機樣本。
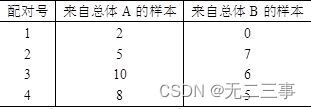
(1)計算A與B各對觀察值之差,再利用得出的差值計算d和sd。
(2)設μ1和μ2分別為總體A和總體B的均值,構造μd=μ1-μ2的95%的置信區間。
解:(1)計算過程如錶7-9所示。
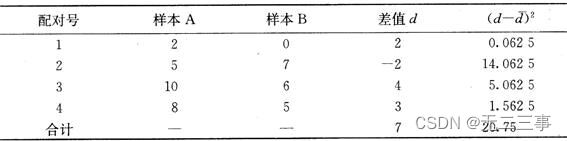
d=7/4=1.75
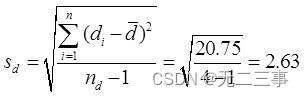
(2)當α=0.05時,t0.05/2(4-1)=3.182。兩個樣本之差μd=μ1-μ2的95%的置信區間為:
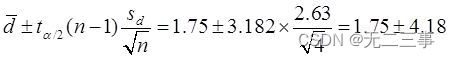
即(-2.43,5.93)。
13一家人才測評機構對隨機抽取的10名小企業的經理人用兩種方法進行自信心測試,得到的自信心測試分數如錶7-10所示。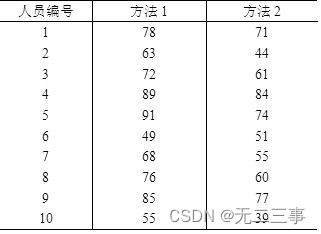
要求:構建兩種方法平均自信心得分之差μd=μ1-μ2的95%的置信區間。
解:根據樣本數據計算得:d=[(78-71)+(63-44)+…+(55-39)]/10=110/10=11
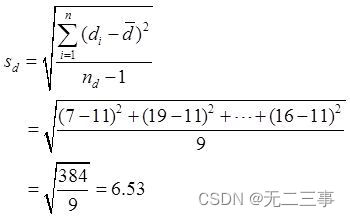
當α=0.05時,t0.05/2(10-1)=2.262。兩種方法平均自信心得分之差μd=μ1-μ2的95%的置信區間為:
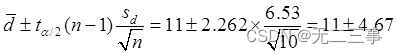
即(6.33,15.67)。
14從兩個總體中各抽取一個n1=n2=250的獨立隨機樣本,來自總體1的樣本比例為p1=40%,來自總體2的樣本比例為p2=30%。要求:
(1)構造π1-π2的90%的置信區間。
(2)構造π1-π2的95%的置信區間。
解:(1)已知:n1=n2=250,p1=40%,p2=30%,α=0.1,z0.1/2=1.645。π1-π2的90%的置信區間為:
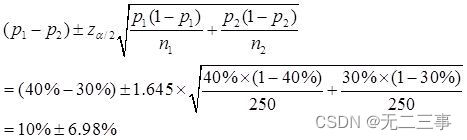
即(3.02%,16.98%)。
(2)α=0.05,z0.05/2=1.96。π1-π2的90%的置信區間為:
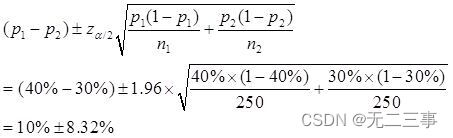
即(1.68%,18.32%)。
15生產工序的方差是工序質量的一個重要度量。當方差較大時,需要對工序進行改進以减小方差。錶7-11是兩部機器生產的袋茶重量(單比特:g)的數據。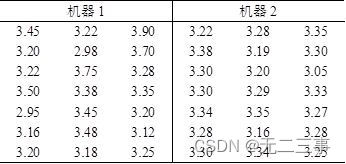
要求:構造兩個總體方差比(σ12/σ22)95%的置信區間。解:根據樣本數據計算得:s12=0.058375,s22=0.005846。當α=0.05時,由Exce1的“FINV”函數計算得:F0.025(21-1,21-1)=2.46,F1-α/2(n1-1,n2-1)=F0.975(21-1,21-1)=0.41。兩個總體方差比σ12/σ22的95%的置信區間為:
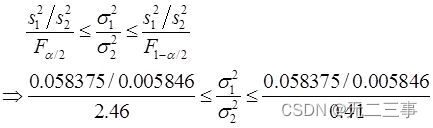
即兩個總體方差比σ12/σ22的95%的置信區間為:4.06≤σ12/σ22≤24.35。
16根據以往的生產數據,某種產品的廢品率為2%。如果置信區間為95%,估計誤差不超過4%,應抽取多少樣本?解:已知:π=2%,E=4%,當α=0.05時,z0.05/2=1.96。應抽取的樣本量為:
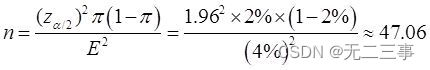
故應至少抽取樣本量為48的樣本。
边栏推荐
- 网络基础详解
- Ucos-iii learning records (11) - task management
- Overview of LNMP architecture and construction of related services
- [experiment index of educator database]
- Mixlab unbounded community white paper officially released
- How to understand the difference between technical thinking and business thinking in Bi?
- 【MySQL数据库的学习】
- 《英特尔 oneAPI—打开异构新纪元》
- JDBC看这篇就够了
- Apache APIs IX has the risk of rewriting the x-real-ip header (cve-2022-24112)
猜你喜欢

HackMyvm靶机系列(5)-warez
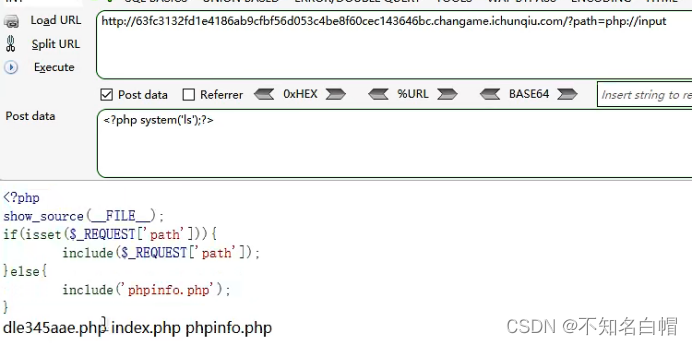
Web vulnerability - File Inclusion Vulnerability of file operation
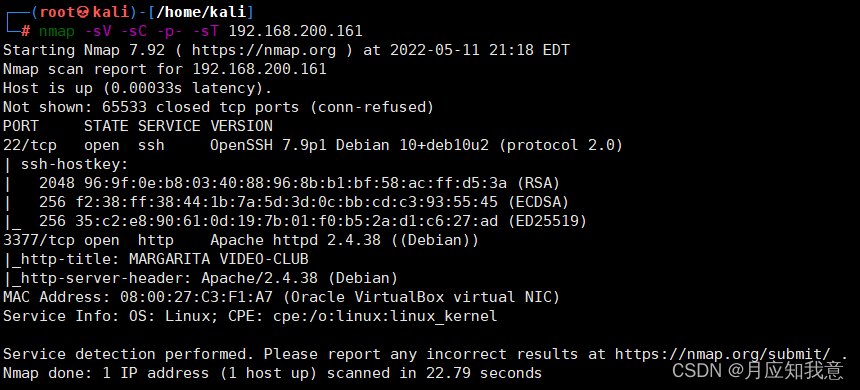
HackMyvm靶机系列(6)-videoclub
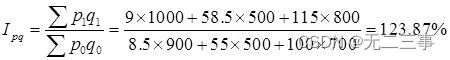
Statistics 8th Edition Jia Junping Chapter 14 summary of index knowledge points and answers to exercises after class

7-7 7003 combination lock (PTA program design)
HackMyvm靶机系列(2)-warrior

Hackmyvm target series (5) -warez
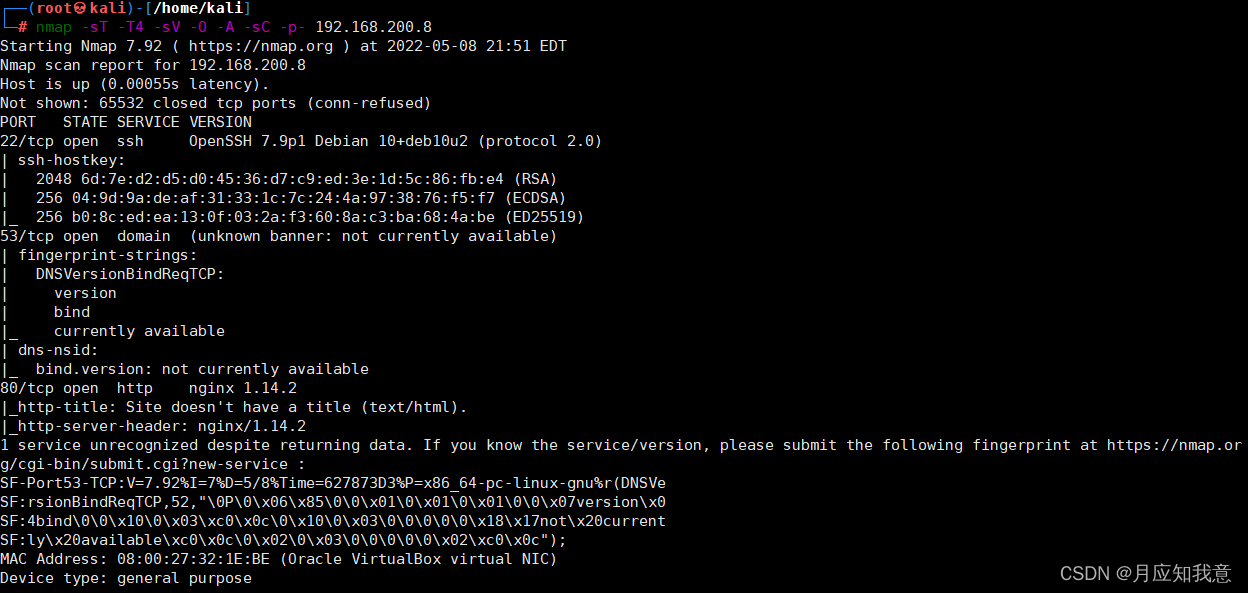
Hackmyvm target series (1) -webmaster
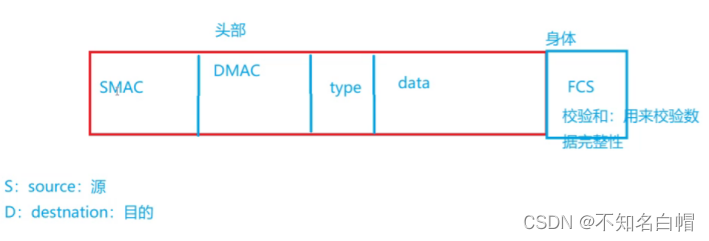
Detailed explanation of network foundation

HackMyvm靶机系列(7)-Tron
随机推荐
搭建域环境(win)
xray与burp联动 挖掘
SystemVerilog discusses loop loop structure and built-in loop variable I
HackMyvm靶机系列(2)-warrior
小程序web抓包-fiddler
7-9 make house number 3.0 (PTA program design)
The difference between layer 3 switch and router
Xray and Burp linked Mining
The most popular colloquial system explains the base of numbers
Hackmyvm target series (2) -warrior
Statistics 8th Edition Jia Junping Chapter 14 summary of index knowledge points and answers to exercises after class
内网渗透之内网信息收集(五)
Library management system
Tencent map circle
HackMyvm靶机系列(7)-Tron
安全面试之XSS(跨站脚本攻击)
captcha-killer验证码识别插件
Callback function ----------- callback
Hackmyvm target series (5) -warez
攻防世界MISC练习区(gif 掀桌子 ext3 )