当前位置:网站首页>OpenGL - Coordinate Systems
OpenGL - Coordinate Systems
2022-07-05 09:18:00 【Farmer er】
From the vertex coordinates to the effect we finally see , There are many coordinate system transformations in the middle :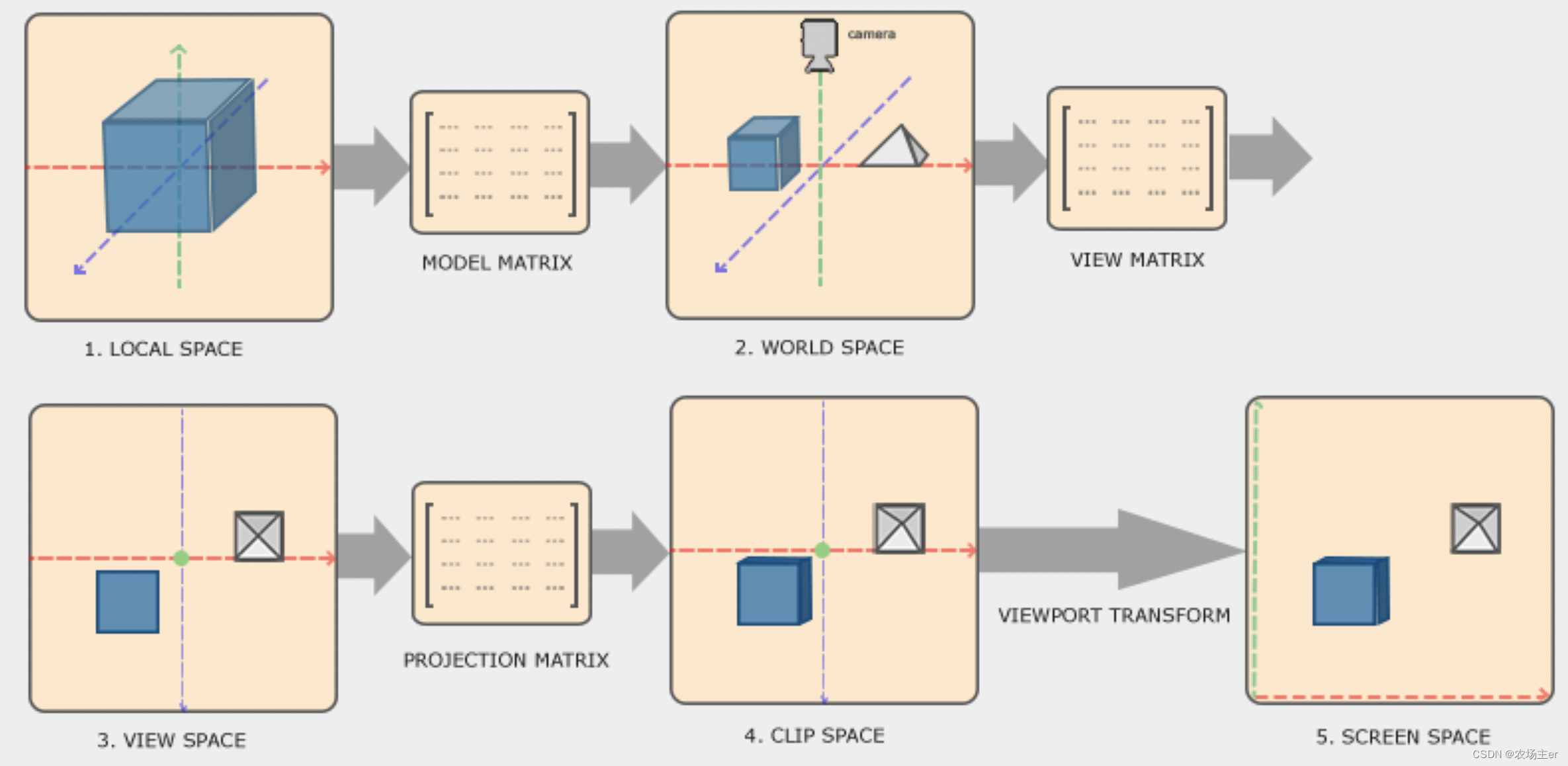
For us , Just focus on three matrices :Vclip=Mprojection⋅Mview⋅Mmodel⋅Vlocal
Mmodel: A matrix that converts local coordinates into world coordinates , Note that the translation at this time is based on the coordinate system of the object itselfMview: Convert the world coordinates from the perspective of the camera , For example, shift to the right , The view will actually pan to the leftMprojection: Project the observation coordinates
Camera/View space
adopt view matrix, Convert the position and direction of the world coordinate system relative to the camera , You can get view space. The position of the camera in the world coordinate system is defined as follows :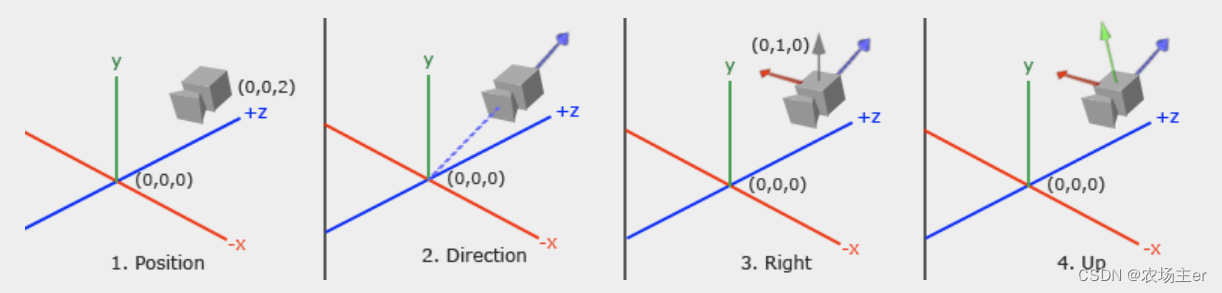
glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);
glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);
glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));
glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);
With the location information , You can calculate that LookAt matrix: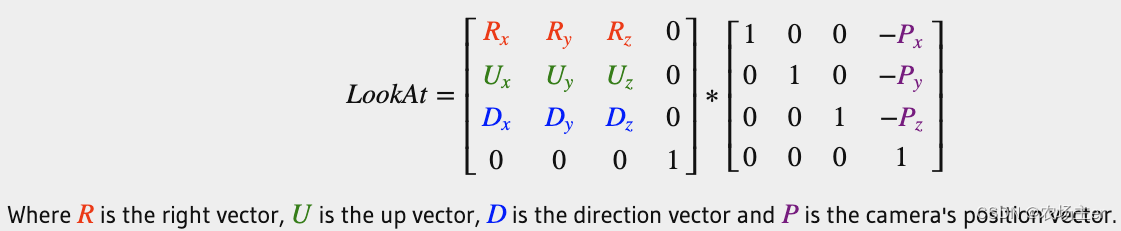
utilize glm This matrix can be constructed more conveniently :
glm::mat4 view;
// Position Target Up
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),
glm::vec3(0.0f, 0.0f, 0.0f),
glm::vec3(0.0f, 1.0f, 0.0f));
Walk around
Moving the view is actually changing the position of the camera , The specific code can refer to ->
Look around
Euler angles
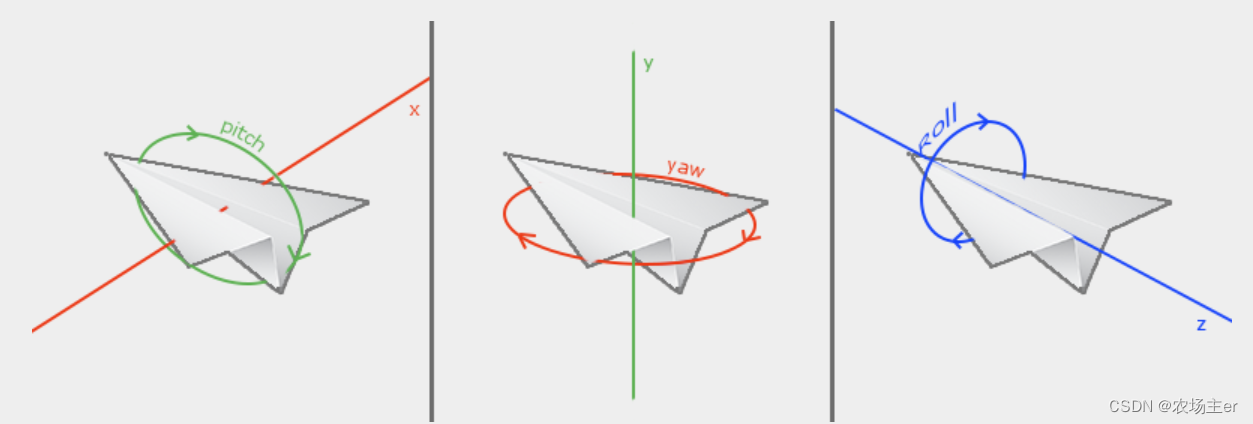
Pitch angle (pitch) It's a corner that describes how we look up or down , You can see in the first picture . The second picture shows Yaw angle (yaw), Indicates the degree to which we look left and right . Roll angle (roll) Represents how we roll the camera , Usually used in spacecraft Cameras .
Moving the mouse left and right changes yaw, Moving up and down changes pitch, The transformed coordinates can be calculated as :
glm::vec3 direction;
// yaw stay xz Plane , pitch stay yz Plane
direction.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));
direction.y = sin(glm::radians(pitch));
direction.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));
Zoom
The effect of enlargement and reduction can be achieved by transmission projection , The specific code can refer to ->
Camera Class
Easy to use , We can encapsulate the functions of the camera -> , Usage method ->
边栏推荐
- An article takes you into the world of cookies, sessions, and tokens
- Kotlin introductory notes (II) a brief introduction to kotlin functions
- Newton iterative method (solving nonlinear equations)
- Introduction Guide to stereo vision (7): stereo matching
- 迁移学习和域自适应
- Kotlin introductory notes (VI) interface and function visibility modifiers
- Huber Loss
- Rebuild my 3D world [open source] [serialization-1]
- [ctfhub] Title cookie:hello guest only admin can get flag. (cookie spoofing, authentication, forgery)
- fs. Path module
猜你喜欢

嗨 FUN 一夏,与 StarRocks 一起玩转 SQL Planner!

LeetCode 31. 下一个排列
![Rebuild my 3D world [open source] [serialization-1]](/img/74/b6253845b43bc18f425d57695fba7c.jpg)
Rebuild my 3D world [open source] [serialization-1]
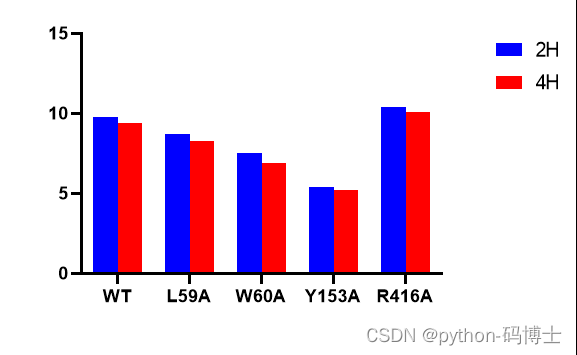
The combination of deep learning model and wet experiment is expected to be used for metabolic flux analysis
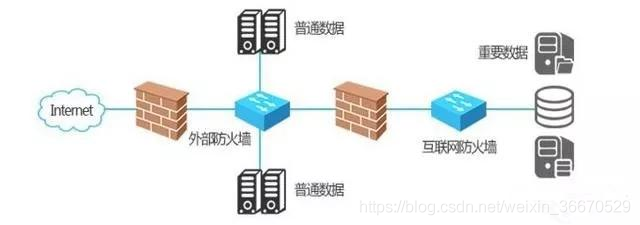
What is a firewall? Explanation of basic knowledge of firewall
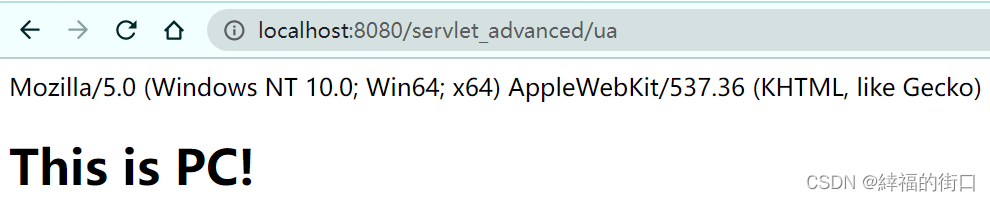
利用请求头开发多端应用
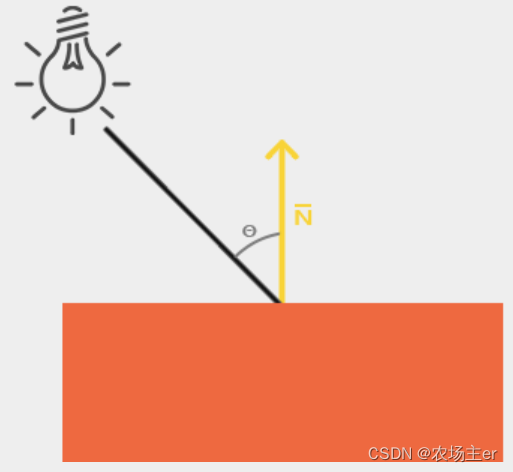
OpenGL - Lighting
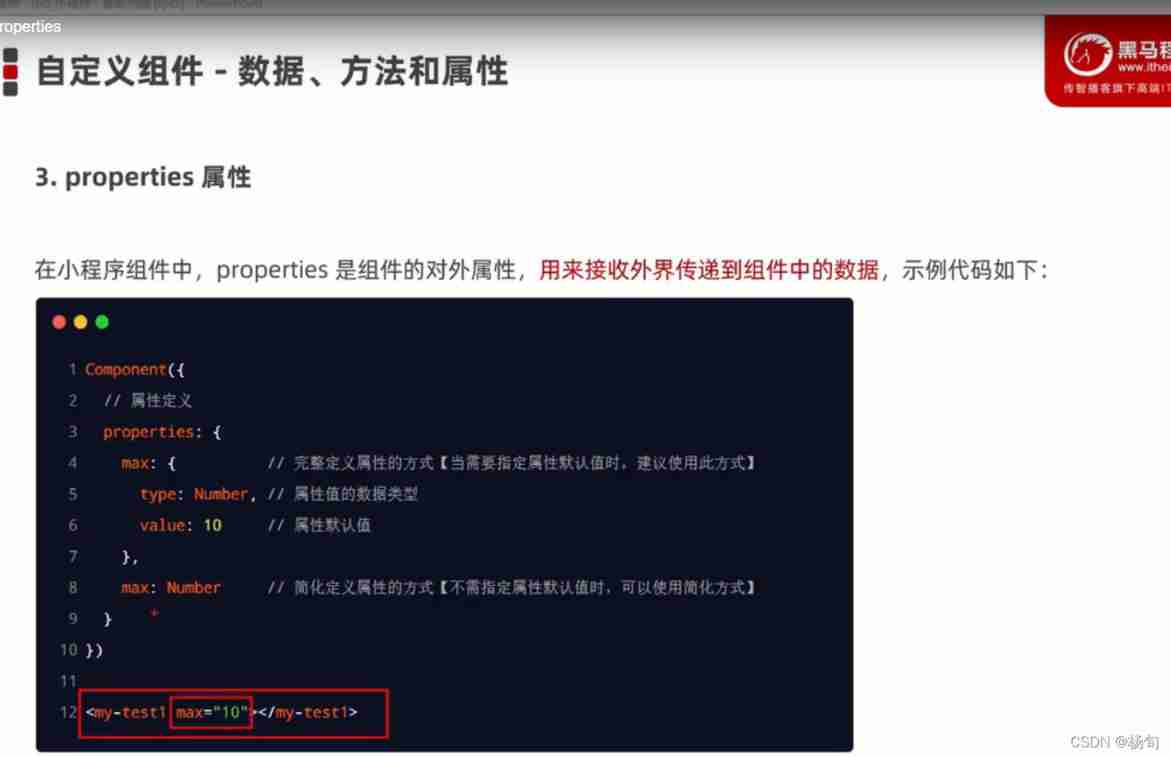
Applet data attribute method
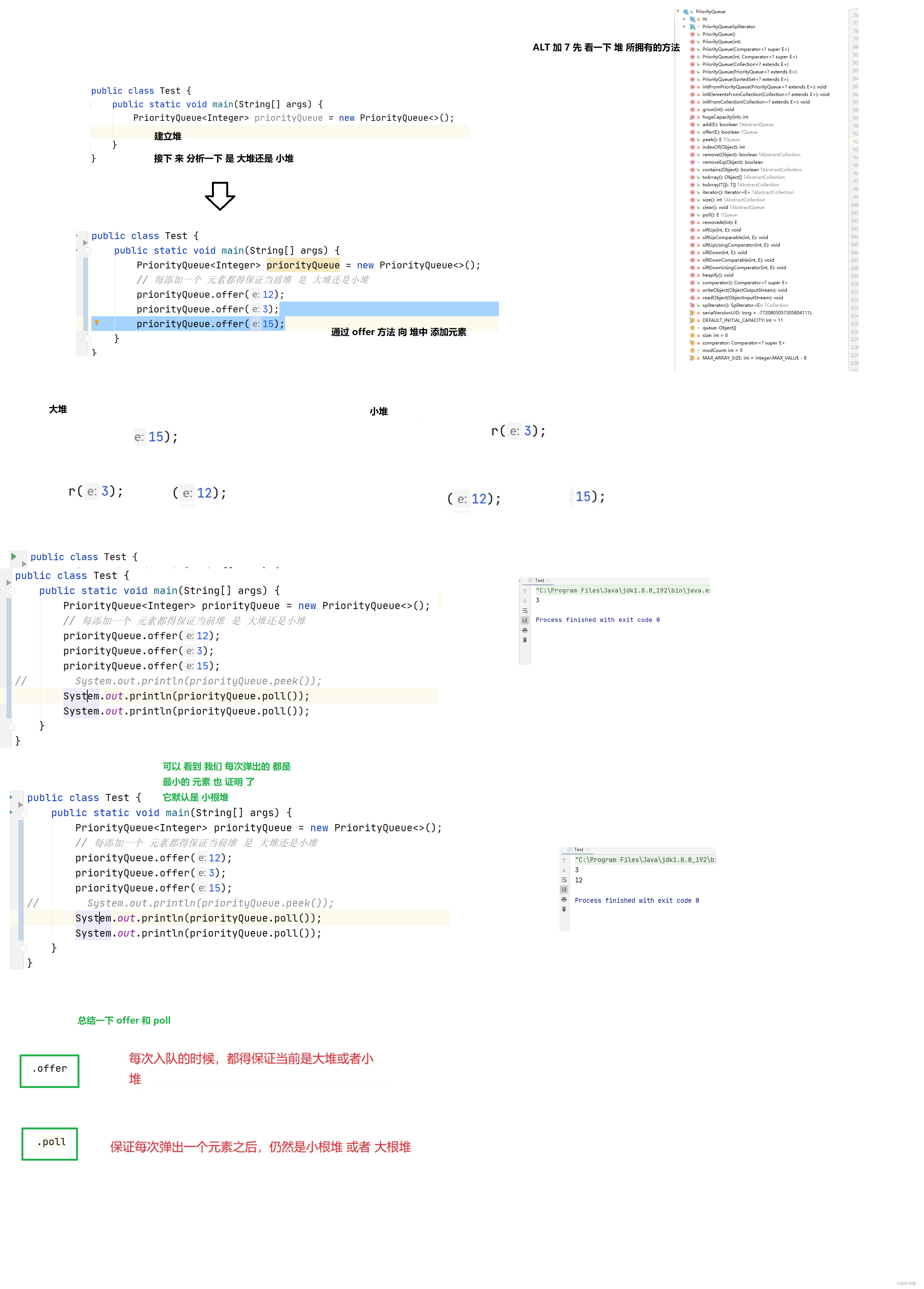
Priority queue (heap)

AUTOSAR from getting started to mastering 100 lectures (103) -dbc file format and creation details
随机推荐
Introduction Guide to stereo vision (2): key matrix (essential matrix, basic matrix, homography matrix)
L'information et l'entropie, tout ce que vous voulez savoir est ici.
C#图像差异对比:图像相减(指针法、高速)
Introduction Guide to stereo vision (7): stereo matching
嗨 FUN 一夏,与 StarRocks 一起玩转 SQL Planner!
Can't find the activitymainbinding class? The pit I stepped on when I just learned databinding
驾驶证体检医院(114---2 挂对应的医院司机体检)
22-07-04 西安 尚好房-项目经验总结(01)
Solution to the problems of the 17th Zhejiang University City College Program Design Competition (synchronized competition)
利用请求头开发多端应用
. Net service governance flow limiting middleware -fireflysoft RateLimit
[ctfhub] Title cookie:hello guest only admin can get flag. (cookie spoofing, authentication, forgery)
Hosting environment API
Kotlin introductory notes (IV) circular statements (simple explanation of while, for)
Priority queue (heap)
Greendao reported an error in qigsaw, could not init daoconfig
【PyTorch Bug】RuntimeError: Boolean value of Tensor with more than one value is ambiguous
Introduction Guide to stereo vision (1): coordinate system and camera parameters
Kotlin introductory notes (VIII) collection and traversal
Node collaboration and publishing