当前位置:网站首页>Ten thousand words detailed eight sorting must read (code + dynamic diagram demonstration)
Ten thousand words detailed eight sorting must read (code + dynamic diagram demonstration)
2022-07-05 07:44:00 【Walk on the horizon with keys】
Catalog
1. The concept of sorting and its application
2.2.1 Direct selection sorting
2.3.2.3 Double finger needling
3.1 Performance test evaluation
3.2 Complexity and stability analysis of sorting algorithm
1. The concept of sorting and its application
1.1 The concept of sequencing
Sort : So called sorting , Is to make a string of records , According to the size of one or some of the keywords , An operation arranged in ascending or descending order .
stability : Assume in the sequence of records to be sorted , There are multiple records with the same keyword , If sorted , The relative order of these records remains the same , In the original sequence ,r[i]=r[j], And r[i] stay r[j] Before , In the sorted sequence ,r[i] Still in r[j] Before , We call this sort algorithm stable ; Otherwise it is called unstable .
Internal sorting : Sorting in which all data elements are placed in memory .
External sorting : Too many data elements to be in memory at the same time , According to the requirements of the sorting process, data sorting cannot be moved between internal and external storage .
1.2 The use of sorting
U.S.News2022 University rankings in

1.3 Common sorting algorithms
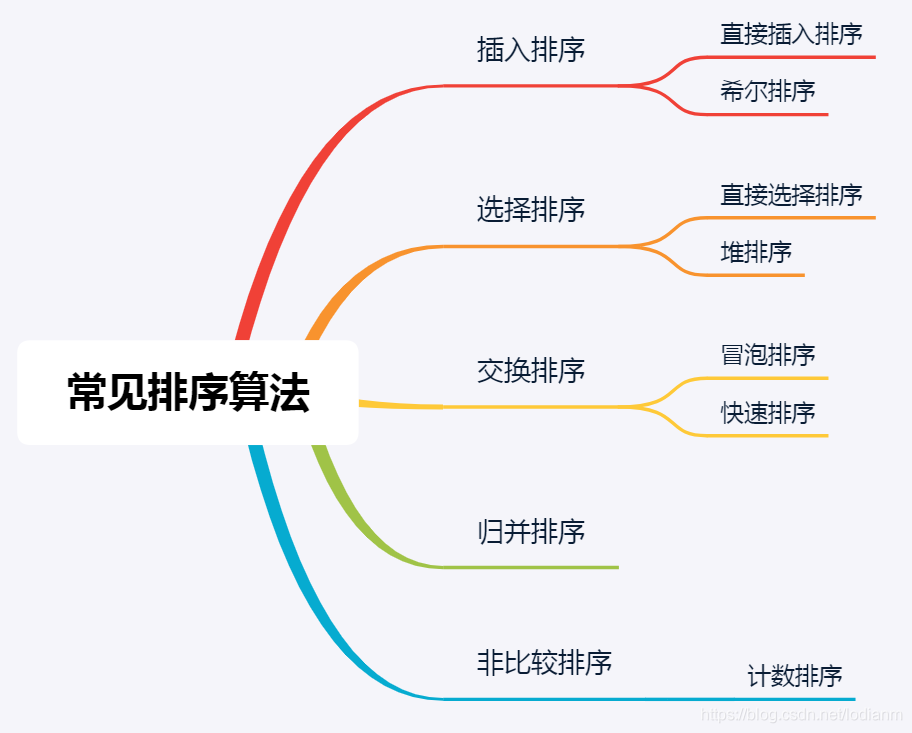
2. Common sorting algorithms
Exchange function , We'll use that later
void Swap(int* p, int* q)
{
int tmp = *p;
*p = *q;
*q = tmp;
}
2.1 Insertion sort
The basic idea
Insert the records to be sorted into an ordered sequence one by one according to their key values , Until all the records are inserted , We get a new ordered sequence . For example, when we play poker with our relatives and friends in the new year , The method of inserting sorting is used in the process of arranging cards .
2.1.1 Direct insert sort
When inserting the i(i>=1) Element time , Ahead array[0],array[1],…,array[i-1] It's in order , Use at this time array[i] The sort code of and array[i-1],array[i-2],… Compare the sort code order of , Find the insertion position array[i] Insert , The elements in the original position move backward in order .
Moving pictures show
Code implementation
// Direct insert sort
void InsertSort(int* a, int n) {
assert(a);
for (int i = 0; i < n - 1 ; i++){
//end It means the tail mark of the order
int end = i;
// Save the number to sort , Otherwise it will be covered
int tmp = a[end + 1];
// As long as the coordinates end The number of is greater than end+1 Number of numbers , that end The number of must be moved backward by one digit
while (end >= 0) {
if (tmp < a[end]) {
a[end + 1] = a[end];
--end;
}
else
break;
}
// Whether it's end<0 sign out , still a[end+1]>a[end] sign out ,a[end+1] The value of should be put in end In the last position of
a[end + 1] = tmp;
}
}Complexity analysis
The best case is that the sorted table itself is ordered , Each element in the array is compared with the previous one , And don't move , The time complexity is O(N), The worst case is that the list to be sorted is in reverse order , Both comparison and movement reach the maximum , The time complexity is O(N^2). Only one auxiliary space is needed , So the spatial complexity is O(1).
2.1.2 Shell Sort
The basic idea
Shell Sort (ShellSort) Also known as “ Reduced delta sort ”. yes 1959 Year by year D.L.Shell Bring up the . The basic idea of this method is : First, the whole sequence of elements to be arranged is divided into several subsequences ( By some other “ The incremental ” The elements of ) Direct insertion sorting is carried out respectively , Then reduce the increment in turn and then sort , The elements in the whole sequence are basically ordered ( The increments are small enough ) when , And then we do a direct insertion sort of all the elements . Because the direct insertion sort is in the case of basically ordered elements ( Close to the best ), Efficiency is very high , Therefore, Hill sorting is more efficient than the first two methods .
Moving pictures show
Hill sort features
1. Hill sort is an optimization of direct insert sort .
2. When gap > 1 It's all pre sorted , The goal is to make arrays more ordered . When gap == 1 when , The array is nearly ordered , This will soon . So on the whole , Can achieve the effect of optimization .
3. The time complexity of Hill sort is not easy to calculate , because gap There are many ways to get the value of , Makes it difficult to calculate , Therefore, the time complexity of hill sorting is not fixed :
Code implementation
// Shell Sort
void ShellSort(int* a, int n) {
int gap = n;
//gap Always greater than or equal to , Greater than 1 Pre sort
while (gap > 1) {
// Each pre sorted gap Is not the same ,gap It's going to get smaller and smaller
gap /= 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0 && a[end] > tmp) {
// As long as the coordinates end The number of is greater than end + gap Number of numbers , that end The number of is going to move backwards gap position
a[end + gap] = a[end];
end -= gap;
}
a[end + gap] = tmp;
}
}
}
Complexity analysis
What increment should be selected is the best , It's still a mathematical problem , So far, no one has found the best incremental sequence , It is difficult to calculate the time complexity , Therefore, the time complexity of Hill sort given in many books is not fixed .
The following two paragraphs on complexity are intercepted from two classic data structure books .《 data structure (C Language version )》— YanWeiMin
《 data structure - Use the face object method and C++ describe 》— Yin renkun
2.2 Selection sort
Each time, select the smallest from the data elements to be sorted ( Or maximum ) An element of , Store at the beginning of the sequence , Until all the data elements to be sorted are finished .
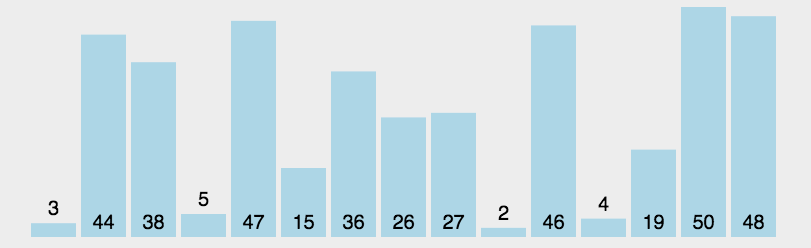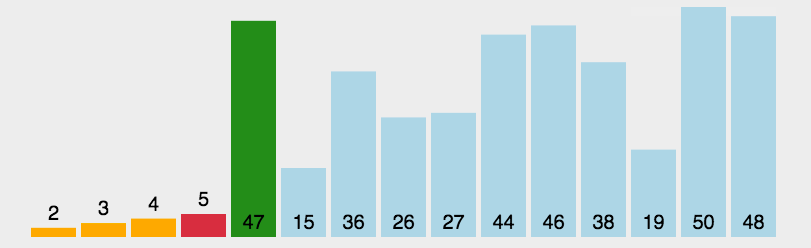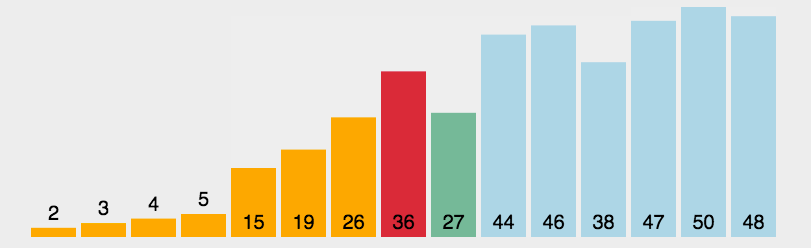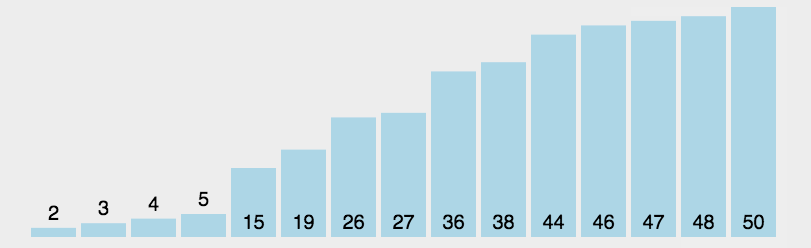
2.2.1 Direct selection sorting
The basic idea
In the element set array[i]--array[n-1] Select the largest key in ( Small ) Data elements , If it's not last of the these elements ( first ) Elements , Then it is combined with the last element in the group ( first ) Element exchange , In the remaining array[i]--array[n-2](array[i+1]--array[n-1]) Collection , Repeat the above steps , Until the set remains 1 Elements
Moving pictures show
Code implementation
void SelectSort(int* a, int n) {
for (int i = 1; i < n; i++) {
// Define the first subscript as the subscript of the minimum
int min = i - 1;
for (int j = i; j < n; j++) {
// If there is a keyword less than the minimum value after it , Just exchange subscripts
if (a[j] < a[min]) {
min = j;
}
}
//min != i-1, Description find the minimum , In exchange for
if (min != i - 1) {
Swap(&a[min], &a[i - 1]);
}
}
}
Complexity analysis
At best or worst , The number of comparisons is the same , The first i The sequence of trips needs to be n-i Sub keyword comparison , So we need to compare 1/2*n(n-1) Time , The best time to exchange 0 Time , Exchange at the worst n-1 Time , The final time complexity is O(N^2), The space complexity is O(1), It can be seen that the sorting efficiency is very poor , It's rarely used in practice .
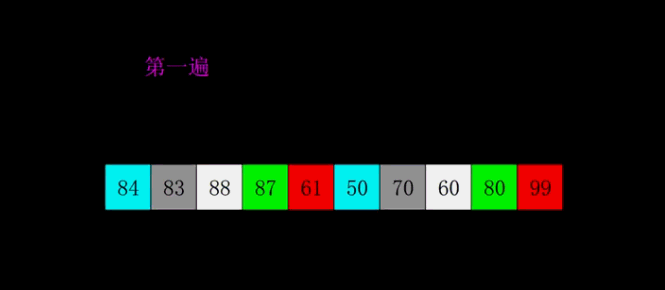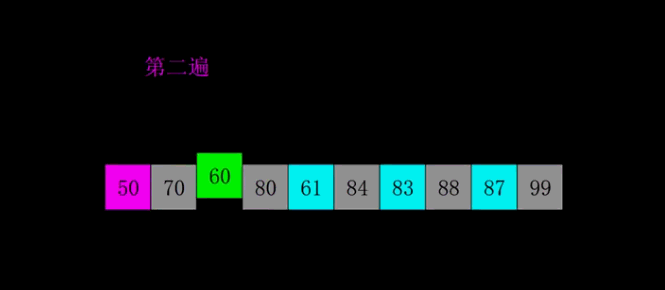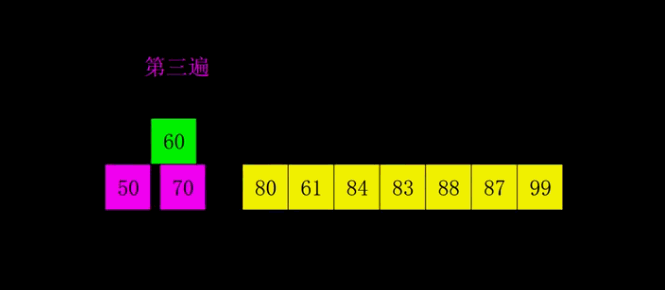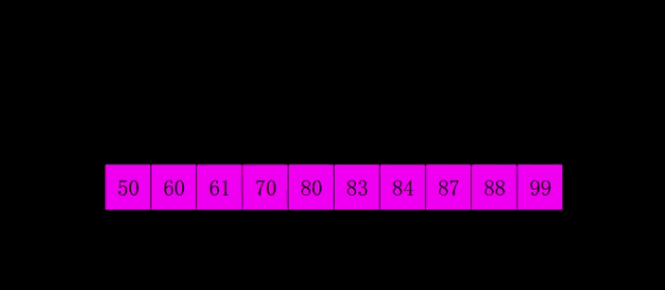
2.2.2 Heap sort
The basic idea
Using stacked trees ( Pile up ) A sort algorithm designed by this data structure , It's a sort of selective sort . It selects data through the heap . It's important to note that in ascending order you have to build lots of , Build small piles in descending order .
Moving pictures show

Code implementation
void AdjustDwon(int* a, int n, int root) {
int parent = root;
int child = parent * 2 + 1;
while (child < n) {
if (child + 1 < n && a[child] < a[child + 1]) {
child++;
}
if (a[child] > a[parent]) {
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void HeapSort(int* a, int n) {
for (int i = (n - 2) / 2; i >= 0; i--) {
AdjustDwon(a, n, i);
}
// Exchange the data at the top of the heap with the data at the end of the heap , In the process of downward adjustment into a lot , However, the data at the end of the heap is not adjusted , Then count the top of the pile
// Data and tail data are exchanged , And so on .
int end = n ;
while (--end > 0) {
Swap(&a[0], &a[end]);
AdjustDwon(a, end, 0);
}
}Complexity analysis
In formal sorting , The first i It takes... To take the top record and rebuild the heap O(nlogi) Time for ( The distance from a node of a complete binary tree to the root node is [log2^k]+1, And need to take n-1 Secondary top record , therefore , The time complexity of rebuilding the heap is O(nlogn), So in general , The time complexity of heap sorting is O(nlogn), The space complexity is O(1).
2.3 Exchange sort
So called exchange , It is to exchange the positions of the two records in the sequence according to the comparison results of the key values of the two records in the sequence , Exchange row
The characteristic of order is : Move the record with large key value to the end of the sequence , Records with smaller key values move to the front of the sequence .
2.3.1 Bubble sort
The basic idea
Compare keywords of adjacent records , If it's in reverse order, swap , Until there are no records in reverse order
Moving pictures show
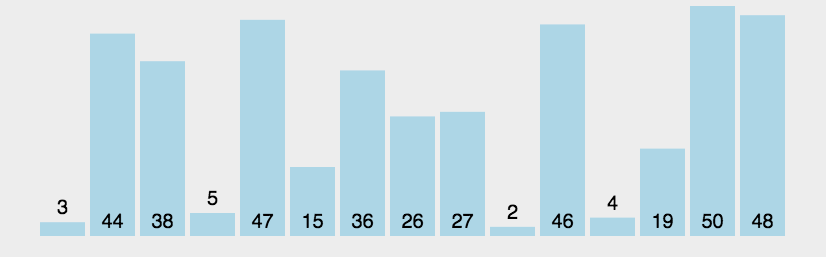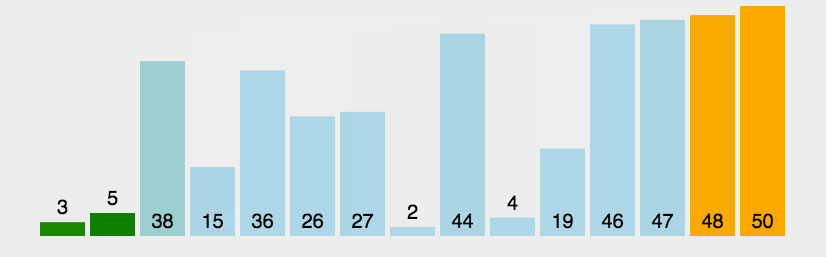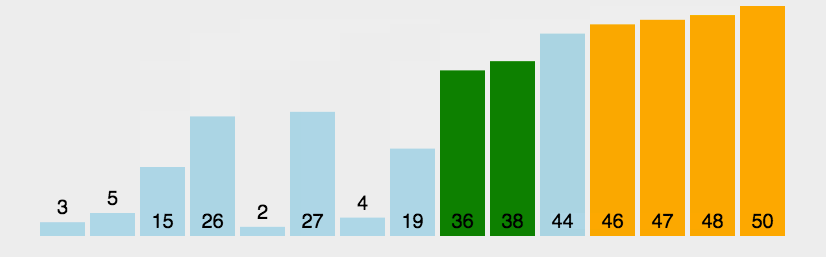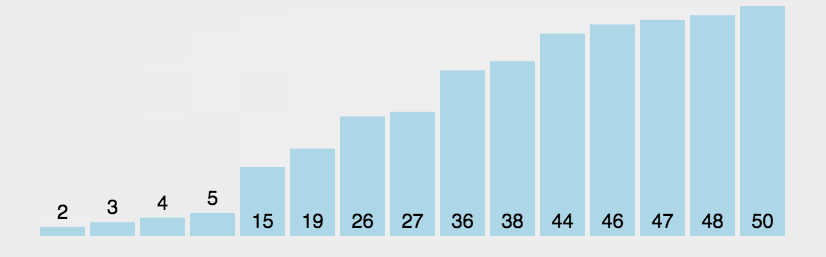
Code implementation
void BubbleSort(int* a, int n) {
for (int i = 1; i < n; i++) {
int flag = 0;
for (int j = n - 1; j >= i; j--) { //j It's a cycle from back to front
if (a[j] < a[j - 1]) {
// If the following number is smaller than the previous one , Just exchange , Each trip will move the small number forward
Swap(&a[j], &a[j - 1]);
flag = 1;
}
}
if (flag == 0) // if flag==0, It means that there is no exchange in this round , The array is already ordered , immediate withdrawal
break;
}
}Complexity analysis
The best situation , That is, the table to be sorted itself is ordered , So we need to compare n-1 Time , No data exchange , The time complexity is O(n), The worst case is that the list to be sorted is in reverse order , Need to compare 1+2+3+...+(n-1)=1/2*n(n-1) Time , So the time complexity is zero O(N^2), The space complexity is O(1).
2.3.2 Quick sort
2.3.2.1Hoare
The basic idea
Use the left and right pointers to point to the head and tail of the array to be sorted , Choose another key value , Generally, the first element is regarded as key value , The right pointer moves to the left , Find the ratio key Elements with small values stop , Then the left pointer moves to the right , Find the ratio key The element with high value stops , Then swap the elements pointed to by the left and right pointers , Continue with the above steps , Until the two hands meet , take key The value of the subscript is exchanged with the value where it meets .
Be careful :
· If we take the header value as our key value , Then we must let the right pointer move first
· If we take the tail value as our key value , Then we must let the left pointer move first
This will ensure that when we finally meet a[left]<a[key],
Moving pictures show 
Single pass sorting
int PartSort1(int* a, int left, int right) {
int key = left;
// Looking for a small
while (left < right) {
while (left < right && a[right] >= a[key]) {
--right;
}
// Looking for big
while (left < right && a[left] <= a[key]) {
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[key]);
return left;
}Sort the whole trip
void QuickSort(int* a, int left, int right) {
// When the interval is divided into only one or none, there is no need to sort
if (left < right) {
int keyi = PartSort1(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
}Complexity analysis
If each time you select key Value is exactly the intermediate value to be sorted , So sort n Key words , Its recursive tree can be approximately seen as a full binary tree , The recursion depth is log2^(n+1), The time complexity required is O(n*logn), The worst case is that the sequence to be sorted is positive or negative , Each partition only gets a subsequence with one record less than the previous partition , Its recursive tree is a skew tree , At this point, recursion is required n-1 Time , Need to compare n-1+n-2+...+2+1=1/2*(n*n-1)), Its time complexity is O(n^2). The complexity of space is logn.
We can optimize this worst case , There are methods :1. You can randomly select key value ,2. You can take the middle of three numbers ,3. Inter cell optimization
Take the middle of three
The basic idea
Take three keywords and sort them first , Pivot the middle number , Usually take the leftmost end 、 The rightmost and middle three numbers
Code implementation
int Threedigit(int* a, int left, int right) {
int mid = (left + right) >> 2;
if (a[left] > a[mid]) {
if (a[mid] > a[right]) {
return mid;
}
else if (a[left] > a[right]) {
return right;
}
else {
return left;
}
}
else {
if (a[mid] < a[right]) {
return mid;
}
else if (a[left] > a[right]) {
return left;
}
else {
return right;
}
}
}
2.3.2.2 Excavation method
The basic idea
Take the first value as key value , Think of it as a pit , Take out the first number and put it in tmp Save the variables , The right pointer moves to the left , Find the ratio key Put a small value into the pit , Line into a new pit , The left pointer looks to the right to find the ratio key Large values are placed in the pit , There are new pits , Until the two hands meet ( The two pointers must meet in the pit ), And then tmp The value in is placed where it meets .
Moving pictures show
Code implementation
Single pass sorting
int PartSort2(int* a, int left, int right) {
int tmp = Threedigit(a, left, right);
Swap(&a[left], &a[tmp]);
int key = a[left];
while (left < right) {
// Looking for a small
while (left < right && a[right] >= key) {
--right;
}
// hold right The value of the position is assigned to left Location ,right The position is the pit
a[left] = a[right];
while (left < right && a[left] <= key) {
++left;
}
//left Pointing ratio key Position of large value , hold left The value of the position is assigned to right,left It's the pit
a[right] = a[left];
}
a[left] = key;
return left;
}Sort the whole trip
void QuickSort(int* a, int left, int right) {
if (left < right) {
int keyi = PartSort1(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
}
2.3.2.3 Double finger needling
The basic idea
You need two pointers , One in front, one in back , Use them separately cur Indicates the front pointer , use prev Represents the back pointer , At the beginning , Regulations cur stay prev The next position of , Or choose the first number as the benchmark , If cur The value of is greater than the reference value , At this time, only cur++, If cur When the pointing position is smaller than the reference value, let's prev++, Judge prev++ Whether it is related to cur Equal position , If not equal , The exchange cur and prev Value , Until the last , We'll exchange prev and key, In this way, the position of the reference value is determined .
Moving pictures show
Code implementation
Single pass sorting
int PartSort3(int* a, int left, int right) {
int tmp = Threedigit(a, left, right);
Swap(&a[left], &a[tmp]);
int prev = left, cur = left + 1, key = left;
while (cur <= right) {
if (a[cur] < a[key] && ++prev != cur) {
Swap(&a[cur], &a[prev]);
}
++cur;
}
Swap(&a[left], &a[prev]);
return prev;
}Sort the whole trip
void QuickSort(int* a, int left, int right) {
if (left < right) {
int keyi = PartSort1(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
}
2.3.2.4 Quick sort non recursive
The first three methods use recursive methods , But recursion is flawed , Many people may think that recursive multiple calls to stack space will affect performance , But now the compiler is optimized very well , Performance is no longer a big problem , The biggest problem is if the recursion depth is too deep , The program itself is OK , But there is not enough stack space , Will cause stack overflow , So it can be written in non recursive form , There are two forms of non recursion :1. Directly change the cycle ( Fibonacci number solution ),2. Use stack storage data to simulate recursive process ( Tree traversal is non recursive 、 Fast non recursive and so on ).
The basic idea
Non recursive here with the help of stack , Put the sections we need to row in a single trip into the stack in turn , Take the interval in the stack in turn and arrange it in a single trip , Then put the sub interval to be processed on the stack , In this cycle , Until the stack is empty, the processing is completed .
Code implementation
void QuickSortNonR(int* a, int left , int right) {
Stack ph;
StackInit(&ph);
StackPush(&ph, left);
StackPush(&ph, right);
while (!StackEmpty(&ph)) {
right = StackTop(&ph);
StackPop(&ph);
left = StackTop(&ph);
StackPop(&ph);
int keyi = PartSort1(a, left, right);
if (left < keyi - 1) {
StackPush(&ph, left);
StackPush(&ph, keyi - 1);
}
if (keyi + 1 < right) {
StackPush(&ph, keyi + 1);
StackPush(&ph, right);
}
}
StackDestory(&ph);
}Complexity analysis
Time complexity :O(n*logn)
Spatial complexity :O(logn)
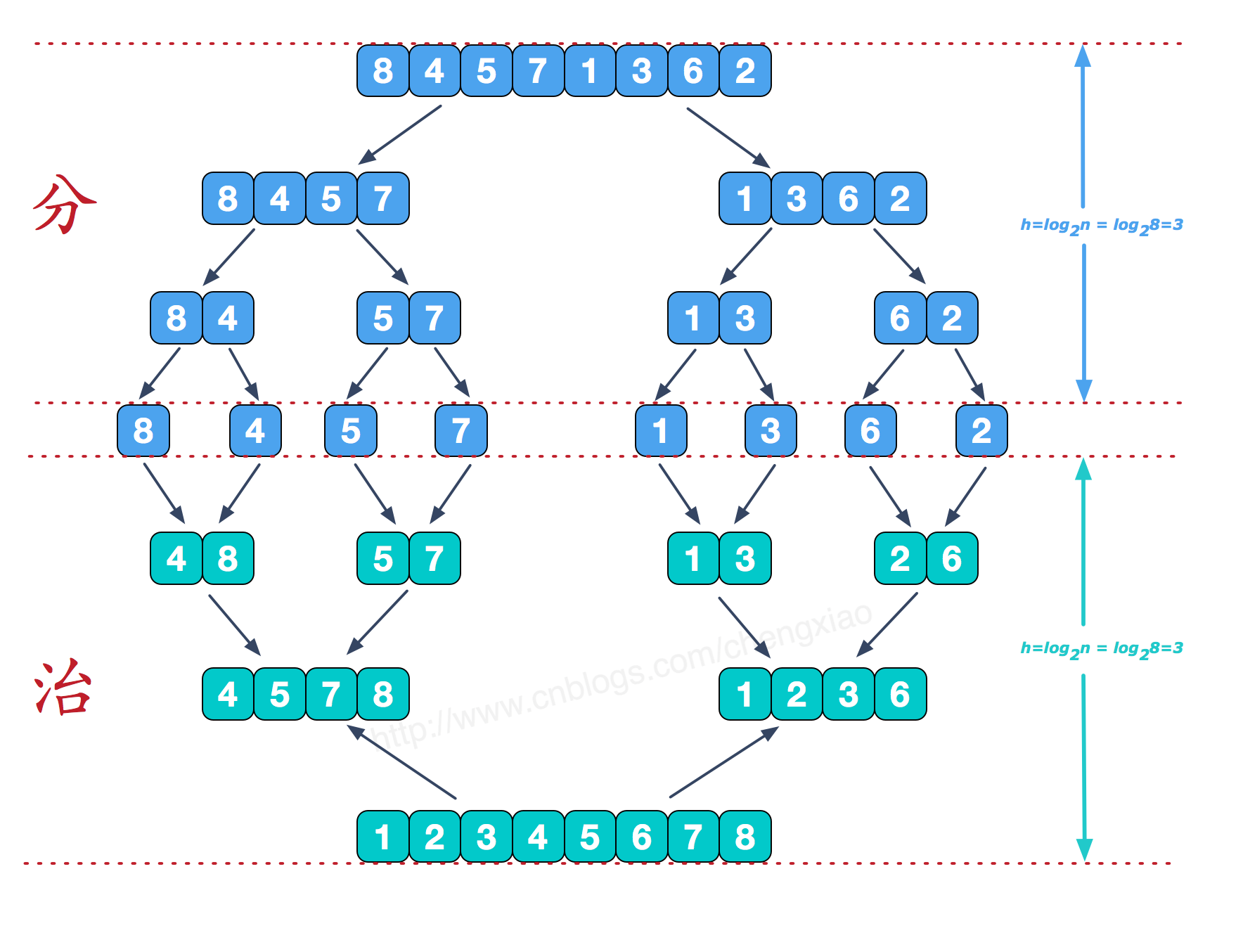
2.4 Merge sort
The basic idea
Merge sort (MERGE-SORT) It is an effective sorting algorithm based on merge operation , The algorithm is a divide-and-conquer method (Divide andConquer) A very typical application . Merges ordered subsequences , You get a perfectly ordered sequence ; So let's make each subsequence in order , Then make the subsequence segments in order . If two ordered tables are merged into one ordered table , It's called a two-way merge .
2.4.1 Recursive merge sort
The core step
Code implementation
void Merge(int* a, int begin1, int end1, int begin2, int end2, int* tmp) {
int i = begin1;
int j = begin1;
while (begin1 <= end1 && begin2 <= end2) {
// The data in the two sections are compared one by one
if (a[begin1] < a[begin2]) {
tmp[i++] = a[begin1++];
}
else {
tmp[i++] = a[begin2++];
}
}
// Coming here means that at least one range has no data , I don't know which section has no data , You need to judge one by one
// If there is still data in the first section, copy it all to tmp in , Explain that the second paragraph is missing
while (begin1 <= end1) {
tmp[i++] = a[begin1++];
}
// If there is still data in the second section, copy it all to tmp in , Explain that the first paragraph is missing
while (begin2 <= end2) {
tmp[i++] = a[begin2++];
}
// End of amalgamation , And then tmp Copy the array data to the original array
for (; j <= end2; j++)
{
a[j] = tmp[j];
}
}
void _MergeSort(int* a, int left, int right, int* tmp) {
// When there is only one left, it returns , To carry on the merge
if (left >= right) {
return;
}
int mid = (left + right) >> 1;
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
// Merge the data in the two sections
Merge(a, begin1, end1, begin2, end2, tmp);
}
void MergeSort(int* a, int n) {
// Open up a tmp Array , Merge in this array
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL) {
perror("MergeSort::malloc");
exit(-1);
}
_MergeSort(a, 0, n-1, tmp);
free(tmp);
}Complexity analysis
Each merge requires the original array to be adjacent to h Merge the ordered sequences of , You need to scan all records in the sequence to be sorted , cost O(N) Time , And from the depth of the complete binary tree , The whole merge sort needs to be done log2^n Time , So the time complexity is zero O(N*logN), You need to open up another array of the same size for merging and recursion with a depth of log2^N Stack space of , So the space complexity is zero O(N+logN)=O(N).
2.4.2 Iterative merge sort
Non recursive iterative method , Avoid recursion when the depth is log2^n Stack space of , Space is just an array used temporarily for merging , So the space complexity is zero O(N), The time complexity is O(N*logN). So when merging and sorting , Try to consider using non recursive methods .
Code implementation
void Merge(int* a, int begin1, int end1, int begin2, int end2, int* tmp) {
int i = begin1;
int j = begin1;
while (begin1 <= end1 && begin2 <= end2) {
// The data in the two sections are compared one by one
if (a[begin1] < a[begin2]) {
tmp[i++] = a[begin1++];
}
else {
tmp[i++] = a[begin2++];
}
}
// Coming here means that at least one range has no data , I don't know which section has no data , You need to judge one by one
// If there is still data in the first section, copy it all to tmp in , Explain that the second paragraph is missing
while (begin1 <= end1) {
tmp[i++] = a[begin1++];
}
// If there is still data in the second section, copy it all to tmp in , Explain that the first paragraph is missing
while (begin2 <= end2) {
tmp[i++] = a[begin2++];
}
// End of amalgamation , And then tmp Copy the array data to the original array
for (; j <= end2; j++)
{
a[j] = tmp[j];
}
}
void MergeSortNonR(int* a, int n) {
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL) {
perror("MergeSort::malloc");
exit(-1);
}
int gap = 1;
while (gap < n) {
for (int i = 0; i <n ; i+=2 * gap) {
int begin1 = i, end1 = i + gap - 1,
begin2 = i + gap, end2 = i + 2 * gap - 1;
// When the last group merged , The second cell does not exist , There is no need to merge
if (begin2 >= n)
break;
// When the last group merged , There are... Between the second cell , But the second interval is not enough gap individual , Need to fix
if (end2 >= n)
end2 = n - 1;
Merge(a, begin1, end1, begin2, end2, tmp);
}
gap *= 2;
}
free(tmp);
}2.5 Count sorting
The basic idea
1. Count the number of occurrences of the same element
2. According to the statistical results, the sequence is recycled into the original sequenceWhen the data is large, we can use relative mapping , Give Way ( This value -min) Add one to the array after , Finally, restore it back .
Moving pictures show
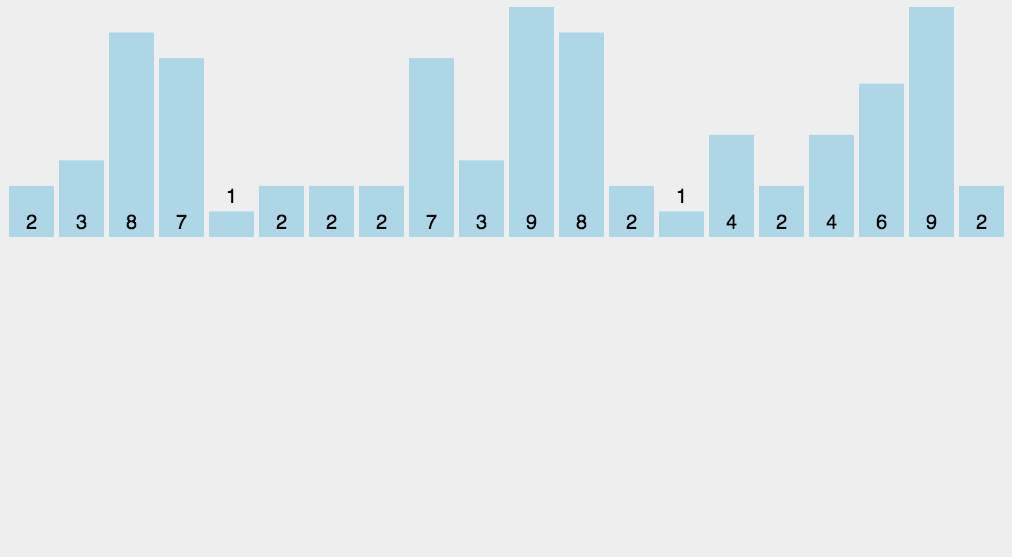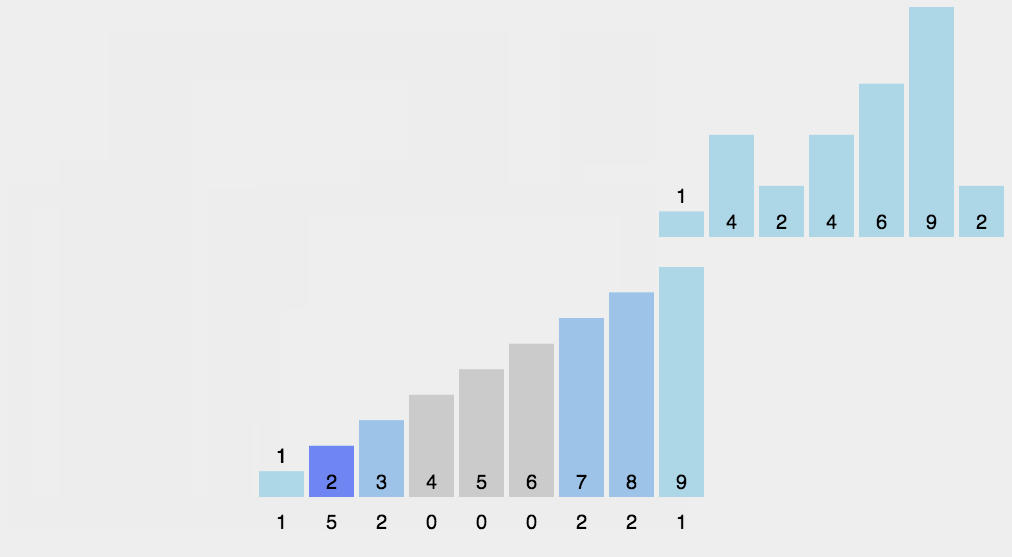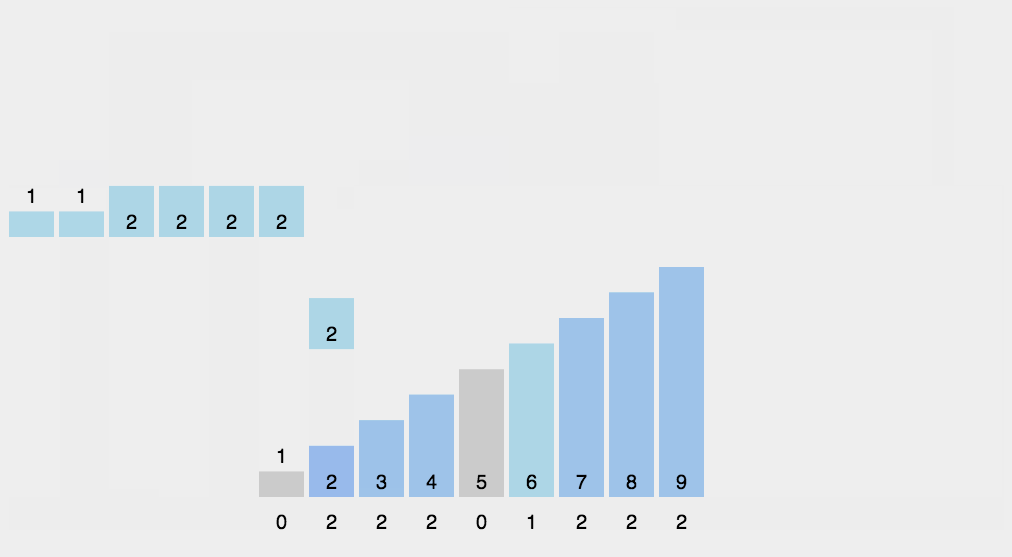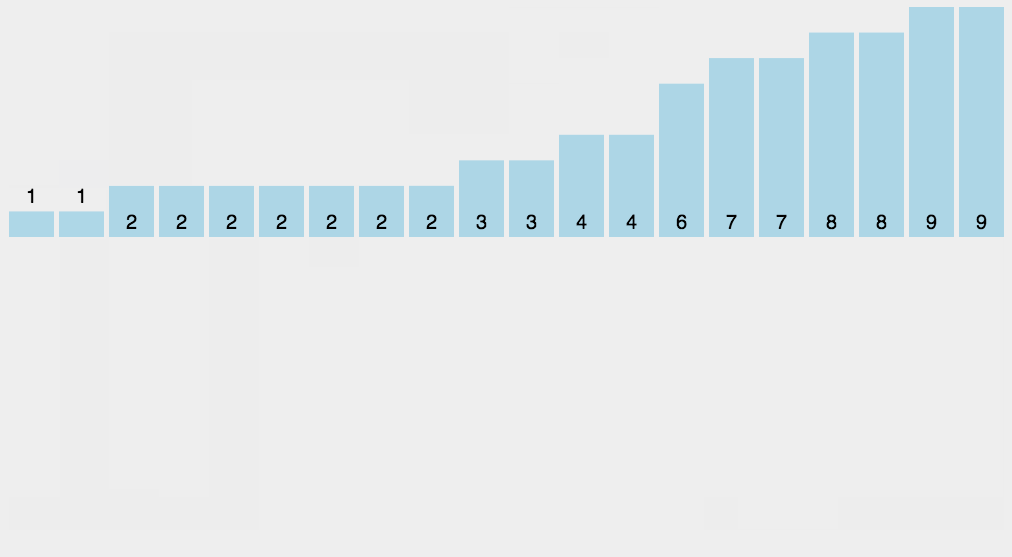
Code implementation
void CountSort(int* a, int n) {
int i = 0;
int min = a[0], max = a[0];
for (i = 0; i < n; i++) {
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
// There are several numbers to count
int num = max - min + 1;
int* count = (int*)malloc(sizeof(int) * num);
if (count == NULL) {
perror("CountSort::malloc");
exit(-1);
}
memset(count, 0, sizeof(int) * num);
// Relative mapping ,count The array records , The number of times each element appears
for (i = 0; i < n; i++) {
count[a[i] - min]++;
}
int j = 0;
// Put each element ( There may be several identical elements ) Copy to the original array from small to large
for (i = 0; i < num; i++) {
while (count[i]--) {
a[j++] = i + min;
}
}
free(count);
}
Complexity analysis
1. When the count sort is in the data range set , It's very efficient , However, the scope of application and scenarios are limited .
2. Time complexity :O(MAX(N, Range ))
3. Spatial complexity :O( Range )
3. Comparison of eight orders
3.1 Performance test evaluation
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
}
int main()
{
TestOP();
return 0;
} 
3.2 Complexity and stability analysis of sorting algorithm
Sorting algorithm | Average time complexity | Worst time complexity | Best time complexity | Spatial complexity | stability |
Bubble sort | O(n²) | O(n²) | O(n) | O(1) | Stable |
Simple selection sort | O(n²) | O(n²) | O(n) | O(1) | unstable |
Direct insert sort | O(n²) | O(n²) | O(n) | O(1) | Stable |
Quick sort | O(nlogn) | O(n²) | O(nlogn) | O(nlogn) | unstable |
Heap sort | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | unstable |
Shell Sort | O(nlogn) | O(ns) | O(n) | O(1) | unstable |
Merge sort | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | Stable |
Count sorting | O(n+k) | O(n+k) | O(n+k) | O(n+k) | Stable |
边栏推荐
猜你喜欢

Build your own random wallpaper API for free
Basic series of SHEL script (III) for while loop
mysql 盲注常见函数
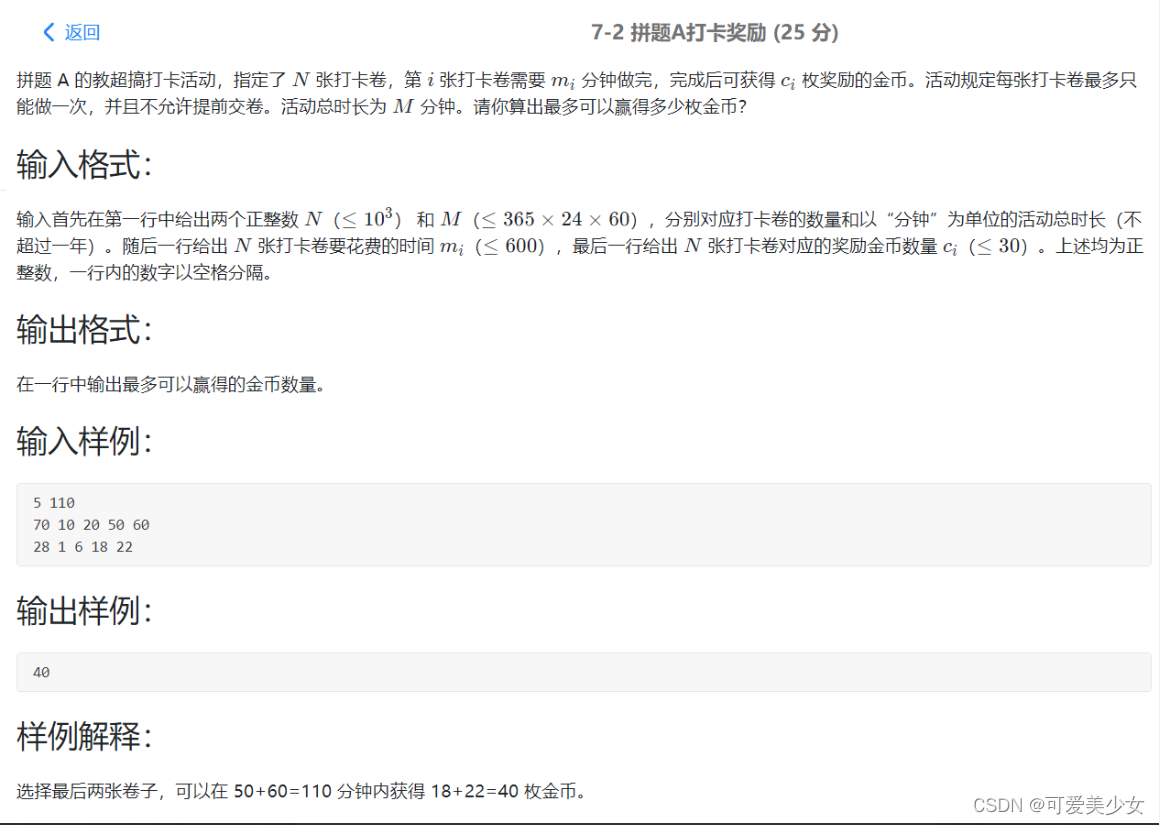
Acwing-宠物小精灵之收服-(多维01背包+正序倒序+两种形式dp求答案)
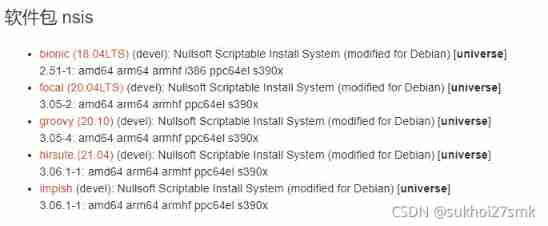
Package ‘*****‘ has no installation candidate
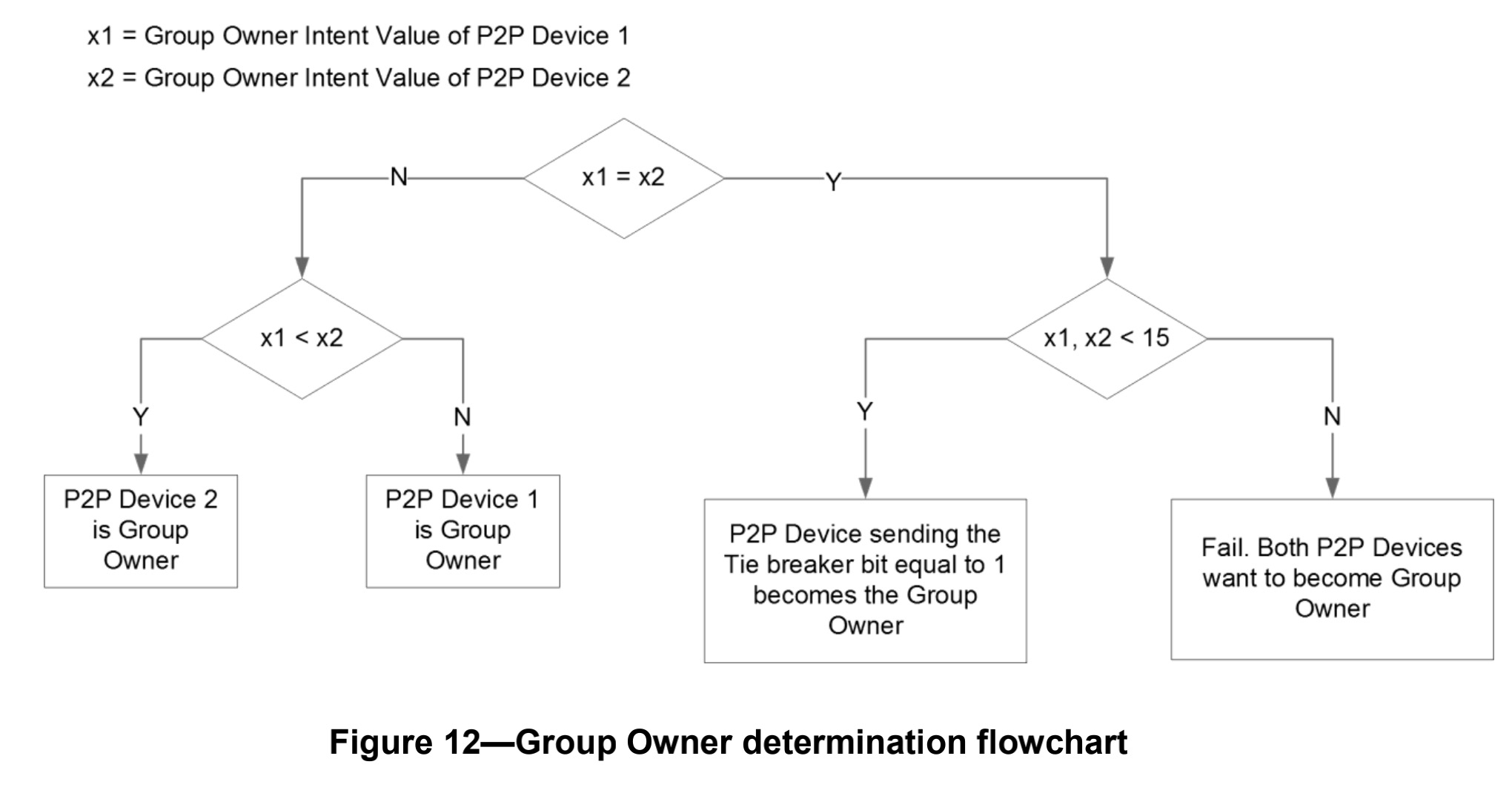
Miracast技术详解(一):Wi-Fi Display
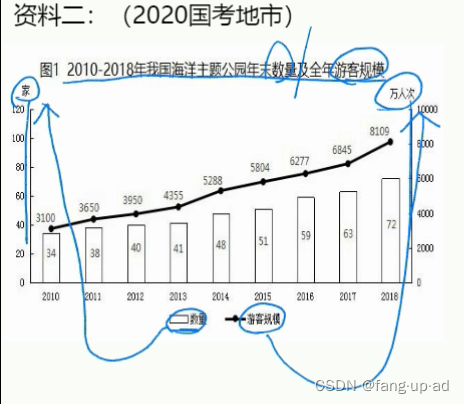
Line test -- data analysis -- FB -- teacher Gao Zhao

Numpy——1. Creation of array
From then on, I understand convolutional neural network (CNN)
II Simple NSIS installation package
随机推荐
Charles- unable to grab bags and surf the Internet
RF ride side door processing of prompt box
When jupyter notebook is encountered, erroe appears in the name and is not output after running, but an empty line of code is added downward, and [] is empty
High end electronic chips help upgrade traditional oil particle monitoring
Daily Practice:Codeforces Round #794 (Div. 2)(A~D)
Typecho adds Baidu collection (automatic API submission plug-in and crawler protocol)
[untitled]
Ugnx12.0 initialization crash, initialization error (-15)
II Simple NSIS installation package
Basic series of SHEL script (II) syntax + operation + judgment
Unforgettable summary of 2021
Opendrive record
CADD课程学习(5)-- 构建靶点已知的化合结构(ChemDraw)
Apple system shortcut key usage
Altium Designer 19.1.18 - 清除测量距离产生的信息
NSIS search folder
Differences between pycharm and idle and process -- join() in vs Code
Pit record of Chmod 2 options in deepin
Day01 markdown log entry tips
Detailed explanation of C language pointer

