Statistics 8th Edition Jia Junping Chapter 7 Summary of knowledge points and answers to exercises after class

One . Examination site induction

The basic principle of parameter estimation

1 confidence interval
（1） The confidence level is 95% The meaning of confidence interval ： All intervals constructed in some way have 95% The interval contains the true value of the population parameter .（2） The higher the confidence is （ That is, the higher the reliability of the estimation ）, Then the confidence interval is correspondingly wider （ That is, the lower the accuracy of estimation ）.
（3） Characteristics of confidence interval ： The confidence interval is affected by the sample , It's random , The true value of the population parameter is fixed . A specific confidence interval “ Always include ” or “ Absolutely does not include ” The true value of the parameter , non-existent “ What is the probability of including the overall parameters ” The problem of .

2 Criteria for evaluating estimators
（1） unbiasedness ： The expected value of the estimator sampling distribution is equal to the estimated population parameter , namely E（θ）＝θ.
（2） effectiveness ： The variance of the estimator should be as small as possible .
（3） Uniformity ： As the sample size increases , The value of the estimator is getting closer and closer to the parameters of the estimated population .

Interval estimation of a population parameter

Two 、 After class exercises and answers

1 Use the following information , Construct the confidence interval of the overall mean .
（1） The population is normally distributed , And known σ＝500,n＝15,x＝8900, The confidence level is 95%.
（2） The population does not obey the normal distribution , And known σ＝500,n＝35,x＝8900, The confidence level is 95%.
（3） The population does not obey the normal distribution ,σ Unknown ,n＝35,x＝8900,s＝500, The confidence level is 90%.
（4） The population does not obey the normal distribution ,σ Unknown ,n＝35,x＝8900,s＝500, The confidence level is 99%.

Explain ：（1） Because the population obeys the normal distribution ,σ＝500,n＝15,x＝8900,α＝0.05,z0.05/2＝1.96. So the overall average μ Of 95% The confidence interval of is ：

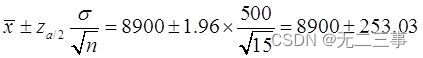
namely （8646.97,9153.03）.
（2） The known population does not obey the normal distribution , but n＝35 Large sample , So we use z statistic , Overall mean μ Of 95% The confidence interval of is ：

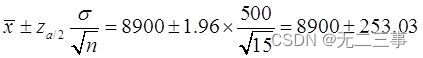
namely （8734.35,9065.65）.
（3） The known population does not obey the normal distribution ,σ Unknown , But because of n＝35 Large sample , So you can use z statistic , Overall mean μ Of 90% The confidence interval of is ：

namely （8760.97,9039.03）.
（4） The known population does not obey the normal distribution ,σ Unknown , But because of n＝35 Large sample , So you can use z statistic , Overall mean μ Of 99% The confidence interval of is ：

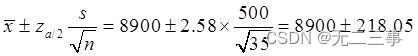
namely （8681.95,9118.05）.

2 In order to understand the time students spend online every day , In the whole school 7500 Students were randomly selected by repeated sampling 36 people , Investigate their time online every day , Get the table 7-3 The data of （ Company ： Hours ）.

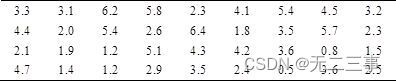
Find the confidence interval of the average online time of college students , The confidence levels are 90%,95% and 99%.

Explain ： It is known that ：n＝36, When α by 0.1,0.05,0.01 when , Corresponding z Values, respectively ：z0.1/2＝1.645,z0.05/2＝1.96,z0.01/2＝2.58
According to the sample data ：

（1） because n＝36 Large sample , So the average online time 90% The confidence interval of is ：

namely （2.88,3.76）.
（2） Average online time 95% The confidence interval of is ：

namely （2.79,3.85）.
（3） Average online time 99% The confidence interval of is ：

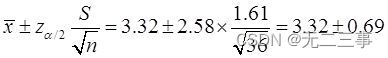
namely （2.63,4.01）.

3 The bagged food produced by an enterprise is packaged by an automatic packaging machine , The standard weight of each bag is 100g, Now we are randomly selected from a batch of products produced on a certain day according to repeated sampling 50 Check the package , The measured weight of each package is shown in the table .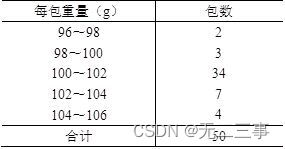

The weight of food package is known from normal distribution , requirement ：
（1） Determine the average weight of this kind of food 95% The confidence interval of .
（2） If the specified food weight is less than 100g It is unqualified , To determine the qualification rate of this batch of food 95% The confidence interval of .

Explain ：（1） It is known that ： The population is normally distributed , but σ Unknown ,n＝50 Large sample ,α＝0.05,z0.05/2＝1.96. According to the grouped sample data ：x＝（97×2＋99×3＋…＋105×4）/50＝101.32

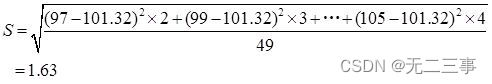
The average weight of this kind of food 95% The confidence interval of is ：

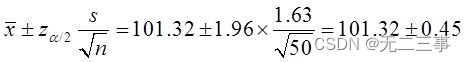
namely （100.87,101.77）.
（2） According to the sample data , The sample qualification rate is p＝45/50＝0.9. The qualified rate of this kind of food 95% The confidence interval of is ：

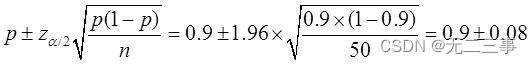
namely （0.82,0.98）.

4 Suppose the population follows a normal distribution , Use the table 7-5 To construct the overall mean μ Of 99% The confidence interval of .

Explain ： It is known that ： The population is normally distributed , but σ Unknown ,n＝25 For small samples ,α＝0.01,t0.01/2（25－1）＝2.797. According to the sample data ：x＝16.128,s＝0.871. Then the overall mean value μ Of 99% The confidence interval of is ：

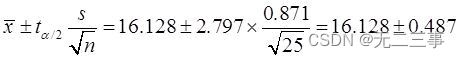
namely （15.64,16.62）.

5 Use the following sample data to build the overall proportion π The confidence interval of .
（1）n＝44,p＝0.51, The confidence level is 99%.
（2）n＝300,p＝0.82, The confidence level is 95%.
（3）n＝1150,p＝0.48, The confidence level is 90%.

Explain ：（1） It is known that ：n＝44,p＝0.51,α＝0.01,z0.01/2＝2.58. The overall ratio π Of 99% The confidence interval of is ：

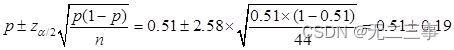
namely （0.32,0.70）.
（2） It is known that ：n＝300,p＝0.82,α＝0.05,z0.05/2＝1.96. The overall ratio π Of 95% The confidence interval of is ：

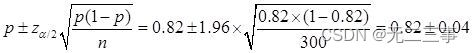
namely （0.78,0.86）.
（3） It is known that ：n＝1150,p＝0.48,α＝0.1,z0.1/2＝1.645. The overall ratio π Of 90% The confidence interval of is ：

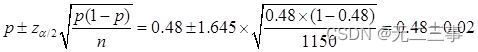
namely （0.46,0.50）.

6 In a household appliance market survey , Randomly selected 200 Households , Investigate whether they own a certain brand of TV . Among them, households with TVs of this brand account for 23%. Find the confidence interval of the overall proportion , The confidence levels are 90% and 95%. Explain ： It is known that ：n＝200,p＝0.23,α by 0.1 and 0.05 when , Corresponding z0.1/2＝1.645,z0.05/2＝1.96.
（1） The overall ratio π Of 90% The confidence interval of is ：

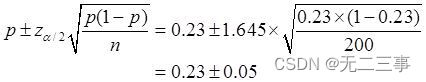
namely （0.18,0.28）.
（2） The overall ratio π Of 95% The confidence interval of is ：

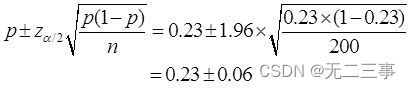
namely （0.17,0.29）.

7 A bank administrator wants to estimate the average monthly deposit of each customer in the bank . He assumes that the standard deviation of all customers' monthly deposits is 1000 element , The required estimation error is 200 Within yuan . The confidence level is 99%, How large a sample should be selected ？ Explain ： It is known that ：σ＝1000, Estimation error E＝200,α＝0.01,z0.01/2＝2.58. Therefore, the sample size to be taken is ：

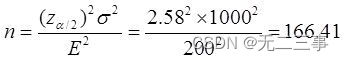
Therefore, we should extract 167 Samples .

8 There are residents in a residential area 500 Household , The community manager is going to adopt a new water supply facility , Want to know whether residents approve . The method of repeated sampling was adopted to randomly select 50 Household , Among them is 32 Household approval ,18 Hu objected .
（1） Find the confidence interval of the proportion of households in favor of the Reform （α＝0.05）.
（2） If the community manager predicts that the proportion of approval can reach 80%, The estimation error does not exceed 10%. How many households should be sampled for investigation （α＝0.05）？

Explain ：（1） It is known that ：n＝50,p＝32/50＝0.64,α＝0.05,z0.05/2＝1.96. Overall, the proportion of households in favor of this reform 95% The confidence interval of is ：

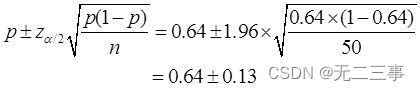
namely （0.51,0.77）.
（2） It is known that ：π＝0.80,α＝0.05,z0.05/2＝1.96. The sample size to be taken is ：

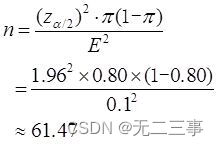
That is, the sample size to be taken is 62 Household .

9 According to the following sample results , Calculate the overall standard deviation σ Of 90% The confidence interval of .
（1）x＝21,s＝2,n＝50.
（2）x＝1.3,s＝0.02,n＝15.
（3）x＝167,s＝31,n＝22.

Explain ：（1） It is known that ：x＝21,s＝2,n＝50,α＝0.1, Look up the table ：χ20.1/2（50－1）＝66.3387,χ21－0.1/2（50－1）＝33.9303. Total variance σ2 The confidence interval of is ：

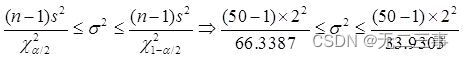
namely 2.95≤σ2≤5.78. The confidence interval of the standard deviation is ：1.72≤σ≤2.40.

（2） It is known that ：x＝1.3,s＝0.02,n＝15,α＝0.1, Look up the table ：χ20.1/2（15－1）＝23.6848,χ21－0.1/2（15－1）＝6.5706. Total variance σ2 The confidence interval of is ：

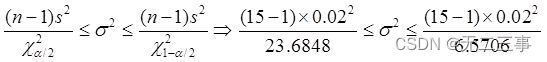
The confidence interval of the standard deviation is ：0.015≤σ≤0.029.
（3） It is known that ：x＝167,s＝31,n＝22,α＝0.1, Look up the table ：χ20.1/2（22－1）＝32.6706,χ21－0.1/2（22－1）＝11.5913. Total variance σ2 The confidence interval of is ：

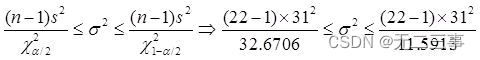
The confidence interval of the standard deviation is ：24.85≤σ≤41.73.

10 Customers often need to wait for a period of time when they go to the bank to transact business , The length of waiting time is related to many factors . such as , The speed at which bank clerks handle business , The way customers wait in line . So , A bank is going to take two queuing methods to test , The first way to queue is ： All customers enter a waiting queue ; The second way of queuing is ： Customers are waiting in three rows at three business windows . To compare which queuing method makes the waiting time of customers shorter , Banks are randomly selected 10 Famous customers , The time they have to wait while doing business （ Company ： minute ）, As shown in the table .

requirement ：
（1） Build the standard deviation of the waiting time of the first queuing method 95% The confidence interval of .
（2） Build the standard deviation of the waiting time of the second queuing method 95% The confidence interval of .
（3） according to （1） and （2） Result , Which way of queuing do you think is better ？

Explain ：（1） It is known that ：n＝10,α＝0.05, Look up the table χ0.05/22（10－1）＝19.0228,χ1－0.05/22（10－1）＝2.7004. According to the way 1 The sample data calculated ：s2＝0.2272. Total variance σ2 The confidence interval of is ：

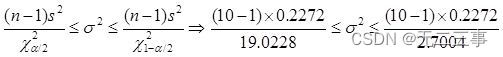
The confidence interval of the standard deviation is ：0.33≤σ≤0.87.
（2） According to the way 2 The sample data calculated ：s2＝3.3183. Total variance σ2 The confidence interval of is ：

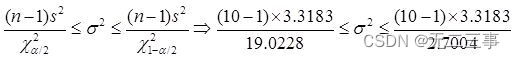
The confidence interval of the standard deviation is ：1.25≤σ≤3.33.
（3） The first way of queuing is better , Because its dispersion is less than that of the second queuing method .

11 Take two independent random samples from two normal populations , Their mean and standard deviation are shown in the table .

（1） set up n1＝n2＝100, seek （μ1－μ2）95% The confidence interval of .
（2） set up n1＝n2＝10,σ12＝σ22, seek （μ1－μ2）95% The confidence interval of .

（3） set up n1＝n2＝10,σ12≠σ22, seek （μ1－μ2）95% The confidence interval of .
（4） set up n1＝10,n2＝20,σ12＝σ22, seek （μ1－μ2）95% The confidence interval of .
（5） set up n1＝10,n2＝20,σ12≠σ22, seek （μ1－μ2）95% The confidence interval of .

Explain ：（1） Because both samples are independent large samples ,σ12 and σ22 Unknown . When α＝0.05 when ,z0.05/2＝1.96, be μ1－μ2 Of 95% The confidence interval of is ：

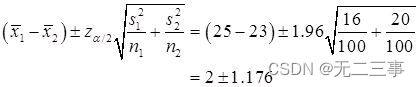
namely （0.824,3.176）.
（2） Because both samples are independent small samples from normal population , When σ12 and σ22 Unknown but σ12＝σ22 when , We need to use the variance of two samples s12 and s22 And to estimate . Combined estimator of population variance sp2 by ：

When α＝0.05 when ,t0.05/2（10＋10－2）＝2.101, be μ1－μ2 Of 95% The confidence interval of is ：

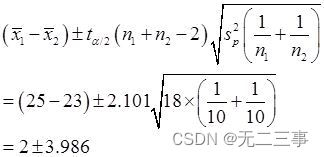
namely （－1.986,5.986）.
（3） Because both samples are independent small samples from normal population ,σ12 and σ22 Unknown and σ12≠σ22,n1＝n2＝n. When α＝0.05 when ,t0.05/2（10＋10－2）＝2.101, be μ1－μ2 Of 95% The confidence interval of is ：

namely （－1.986,5.986）.
（4） Because both samples are independent small samples from normal population ,σ12 and σ22 Unknown but σ12＝σ22,n1≠n2. We need to use the variance of two samples s12 and s22 To estimate . Combined estimator of population variance sp2 by ：

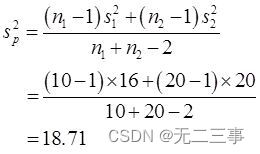
When α＝0.05 when ,t0.05/2（10＋20－2）＝2.048. therefore ,μ1－μ2 Of 95% The confidence interval of is ：

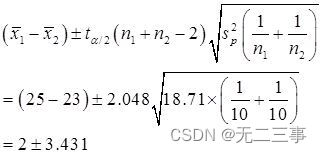
namely （－1.431,5.431）.

（5） Because both samples are independent small samples from normal population ,σ12 and σ22 Unknown and σ12≠σ22,n1≠n2. therefore ,μ1－μ2 Of 95% The confidence interval of is ：

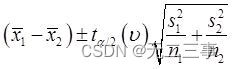
The degrees of freedom are calculated as follows ：

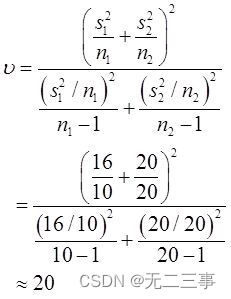
When α＝0.05 when ,t0.05/2（20）＝2.086.μ1－μ2 Of 95% The confidence interval of is ：

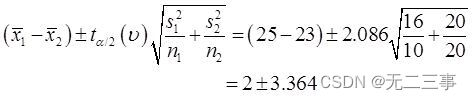
namely （—1.364,5.364）.

12 surface 7-8 By 4 A random sample consisting of observations .

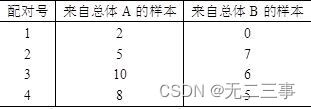
（1） Calculation A And B The difference between each pair of observations , Then use the difference to calculate d and sd.
（2） set up μ1 and μ2 They are the overall A And overall B The average of , structure μd＝μ1－μ2 Of 95% The confidence interval of .

Explain ：（1） The calculation process is shown in table 7-9 Shown .

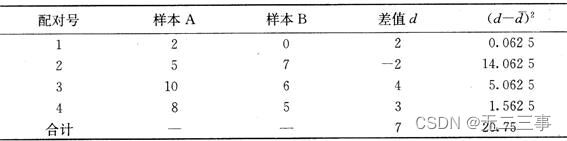
 d＝7/4＝1.75

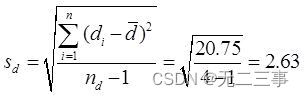
（2） When α＝0.05 when ,t0.05/2（4－1）＝3.182. The difference between the two samples μd＝μ1－μ2 Of 95% The confidence interval of is ：

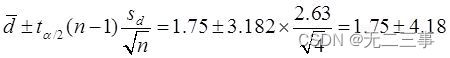
namely （－2.43,5.93）.

13 A talent evaluation organization randomly selected 10 Managers of small businesses use two methods to test their self-confidence , The self-confidence test scores obtained are shown in the table 7-10 Shown .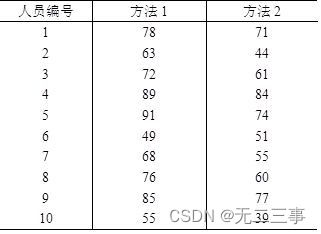

requirement ： Build the difference between the average self-confidence scores of the two methods μd＝μ1－μ2 Of 95% The confidence interval of .

Explain ： According to the sample data ：d＝[（78－71）＋（63－44）＋…＋（55－39）]/10＝110/10＝11

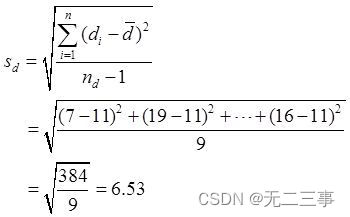
When α＝0.05 when ,t0.05/2（10－1）＝2.262. The difference between the average self-confidence scores of the two methods μd＝μ1－μ2 Of 95% The confidence interval of is ：

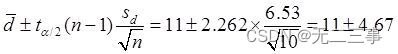
namely （6.33,15.67）.

14 Take one from each of the two populations n1＝n2＝250 Independent random samples , From the whole 1 The sample proportion of is p1＝40%, From the whole 2 The sample proportion of is p2＝30%. requirement ：
（1） structure π1－π2 Of 90% The confidence interval of .

（2） structure π1－π2 Of 95% The confidence interval of .

Explain ：（1） It is known that ：n1＝n2＝250,p1＝40%,p2＝30%,α＝0.1,z0.1/2＝1.645.π1－π2 Of 90% The confidence interval of is ：

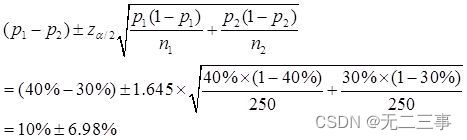
namely （3.02%,16.98%）.
（2）α＝0.05,z0.05/2＝1.96.π1－π2 Of 90% The confidence interval of is ：

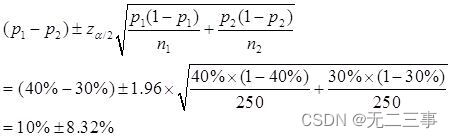
namely （1.68%,18.32%）.

15 The variance of production process is an important measure of process quality . When the variance is large , The process needs to be improved to reduce variance . surface 7-11 It's the weight of tea bags produced by two machines （ Company ：g） The data of .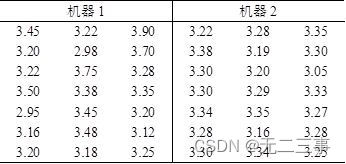

requirement ： Construct two population variance ratios （σ12/σ22）95% The confidence interval of . Explain ： According to the sample data ：s12＝0.058375,s22＝0.005846. When α＝0.05 when , from Exce1 Of “FINV” The function calculates ：F0.025（21－1,21－1）＝2.46,F1－α/2（n1－1,n2－1）＝F0.975（21－1,21－1）＝0.41. The variance ratio of two populations σ12/σ22 Of 95% The confidence interval of is ：

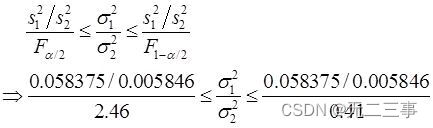
That is, the variance ratio of two populations σ12/σ22 Of 95% The confidence interval of is ：4.06≤σ12/σ22≤24.35.

16 According to previous production data , The scrap rate of a product is 2%. If the confidence interval is 95%, The estimation error does not exceed 4%, How many samples should be taken ？ Explain ： It is known that ：π＝2%,E＝4%, When α＝0.05 when ,z0.05/2＝1.96. The sample size to be taken is ：

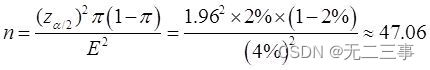
Therefore, the sample size should be at least 48 The sample of .