当前位置:网站首页>《统计学》第八版贾俊平第十二章多元线性回归知识点总结及课后习题答案
《统计学》第八版贾俊平第十二章多元线性回归知识点总结及课后习题答案
2022-07-06 09:23:00 【无二三事】
目录
一、知识框架
二、练习题
1根据表12-2的数据用Excel进行回归,并对回归结果进行讨论,计算x1=200,x2=7时y的预测值。
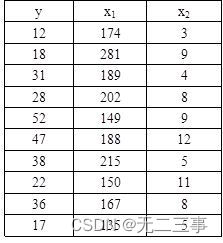
解:由Excel输出的回归结果,如表所示。
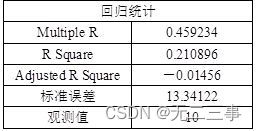
回归结果
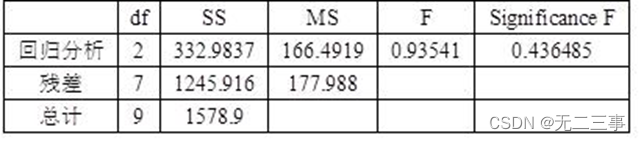
方差分析
 所以回归方程为:y=25.0287-0.04971x1+1.928169x2。
所以回归方程为:y=25.0287-0.04971x1+1.928169x2。
其中β1=-0.04971表示,在x2不变的条件下,x1每增加1个单位,y平均下降0.04971个单位;β2=1.928169表示,在x1不变的条件下,x2每增加1个单位,y平均增加1.928169个单位。判定系数R2=21.09%,表示在因变量的变差中能够被y与x1和x2之间的线性关系所解释的比例为21.09%。由于这一比例很低,表明回归方程的拟合程度很差。估计标准误差se=13.34122,预测误差也较大。方差分析表显示,Significance F=0.436485>α=0.05,表明y与x1和x2之间的线性关系不显著。用于回归系数检验的P值均大于α=0.05,两个回归系数均不显著。当x1=200,x2=7时,y的预测值为:y=25.0287-0.04971×200+1.928169×7=28.58。
2一家电器销售公司的管理人员认为,月销售收入是广告费用的函数,并想通过广告费用对月销售收入作出估计。
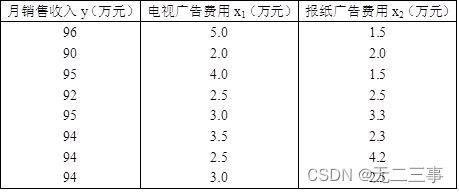
要求:
(1)用电视广告费用作自变量,月销售收入作因变量,建立估计的回归方程。
(2)用电视广告费用和报纸广告费用作自变量,月销售收入作因变量,建立估计的回归方程。
(3)上述(1)和(2)所建立的估计的回归方程,电视广告费用的系数是否相同?对其回归系数分别进行解释。
(4)根据问题(2)所建立的估计的回归方程,在销售收入的总变差中,被估计的回归方程所解释的比例是多少?
(5)根据问题(2)所建立的估计的回归方程,检验回归系数是否显著(α=0.05)。
解:(1)用电视广告费用作自变量,月销售收入作因变量,由Excel输出的回归结果如表所示。
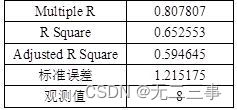
回归结果
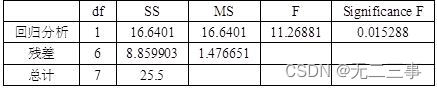
方差分析表

所以估计的回归方程为:y=88.63768+1.603865x1。
(2)用电视广告费用和报纸广告费用作自变量,月销售收入作因变量,由Excel输出的回归结果所示。
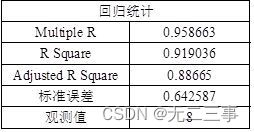
回归结果
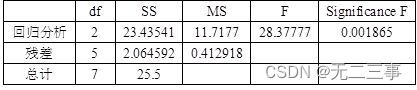
方差分析表

所以估计的回归方程为:y=83.23009+2.290184x1+1.300989x2。
(3)(1)和(2)所建立的估计的回归方程中,电视广告费用的系数不相同。
在(1)的回归方程中,回归系数β1=1.603865表示:电视广告费用每增加1万元,月销售收入平均增加1.603865万元;在(2)的回归方程中,回归系数β1=2.290184表示:在报纸广告费用不变的条件下,电视广告费用每增加1万元,月销售收入平均增加2.290184万元。
(4)问题(2)中,R2=91.9036%,Ra2=88.665%,表明在销售收入的总变差中,被估计的回归方程所解释的比例为88.665%。
(5)问题(2)中,β1的P值0.000653,β2的P值=0.009761,均小于α=0.05,故两个回归系数均显著。
3某农场通过试验取得早稻收获量与春季降雨量和春季温度的数据如表所示。
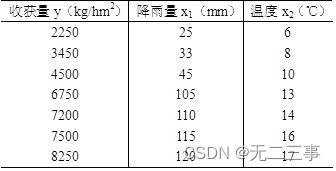
要求:
(1)试确定早稻收获量对春季降雨量和春季温度的二元线性回归方程。
(2)解释回归系数的实际意义。
(3)根据你的判断,模型中是否存在多重共线性?
解:(1)由Excel输出的回归结果如表所示。
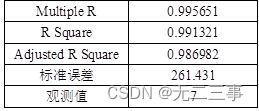
回归结果
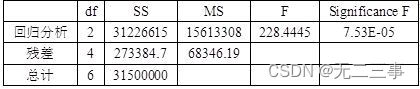
方差分析表
所以早稻收获量对春季降雨量和春季温度的二元线性回归方程为:
y=-0.5910+22.3865x1+327.6717x2
(2)回归系数β1=22.3865表示,在温度不变的条件下,降雨量每增加1mm,小麦收获量平均增加22.3865kg/hm2;回归系数β2=327.6717表示,在降雨量不变的条件下,温度每增加1℃,小麦收获量平均增加327.6717kg/hm2。
(3)从降雨量和温度与收获量的关系看,两个变量与收获量之间都存在较强的关系,而且从表12-16的数据来看,温度与降雨量之间也存在较强的关系,因此,模型中可能存在多重共线性。
4一家房地产评估公司想对某城市的房地产销售价格(y)与地产的评估价值(x1)、房产估价(x2)和使用面积(x3)建立一个模型,以便对销售价格作出合理预测。为此,它收集了20栋住宅的房地产评估数据,如表所示。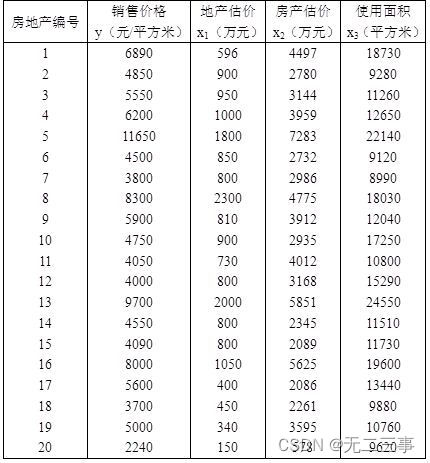
用Excel进行回归,回答下面的问题:
(1)写出估计的多元回归方程。
(2)在销售价格的总变差中被估计的回归方程所解释的比例是多少?
(3)检验回归方程的线性关系是否显著(α=0.05)。
(4)检验各回归系数是否显著(α=0.05)。
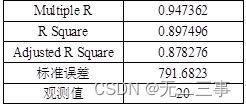
解:(1)由Excel输出的回归结果如表所示。
回归结果
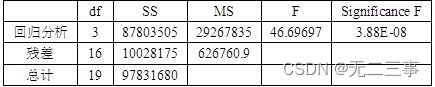
方差分析表
所以估计的多元回归方程为:y=148.7005+0.8147x1+0.8210x2+0.1350x3
(2)多元线性回归分析中,应采用调整的判定系数来度量回归模型的拟合优度,调整的判定系数Ra2=87.83%,表明销售价格的总变差中,被估计的回归方程所解释的比例为87.83%。
(3)由于Significance F=3.88E-08<α=0.05,因此回归方程的线性关系显著。
(4)β1的P值=0.1311>α=0.05,不显著;β2的P值=0.0013≤α=0.05,显著;β3的P值=0.0571>α=0.05,不显著。
5表12-21是随机抽取的15家大型商场销售的同类产品的有关数据(单位:元)。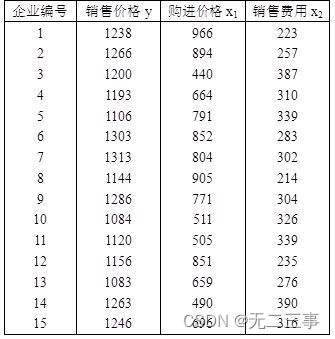
要求:
(1)计算y与x1、y与x2之间的相关系数,是否有证据表明销售价格与购进价格、销售价格与销售费用之间存在线性关系?
(2)根据上述结果,你认为用购进价格和销售费用来预测销售价格是否有效?
(3)用Excel进行回归,并检验模型的线性关系是否显著(α=0.05)。
(4)解释判定系数R2,所得结论与问题(2)中是否一致?
(5)计算x1与x2之间的相关系数,所得结果意味着什么?
(6)模型中是否存在多重共线性?你对模型有何建议?
解:(1)由Excel的“CORREL”函数计算的系数
![]()
![]()
检验的统计量分别为:
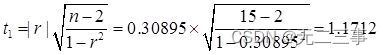
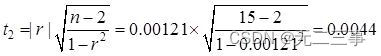
取α=0.05,t0.05/2(15-2)=2.160。由于检验统计量t1=1.1712<tα/2=2.160,t2=0.0044<tα/2=2.160。因此没有证据表明销售价格与购进价格、销售价格与销售费用之间存在线性关系。
(2)由于没有证据表明销售价格与购进价格、销售价格与销售费用之间存在线性关系,因此用购进价格和销售费用来预测销售价格是没有用的。
(3)由Excel输出的回归结果,如表所示。
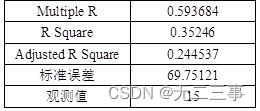
回归结果
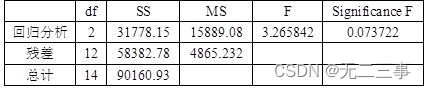
方差分析表

所以回归方程为:y=375.6018+0.5378x1+1.4572x2
由于Significance F=0.073722>α=0.05,线性关系不显著。
(4)R2=35.25%,Ra2=24.45%,表明销售价格在总变差中,销售被估计的回归方程所解释的比例为24.45%,说明线性关系不显著,所得结论与问题(2)一致。
(5)由Excel的“CORREL”函数计算的系数
![]()
两个自变量高度负相关。
(6)由于两个自变量高度负相关,因此模型中存在多重共线性,建议将一个自变量从模型中剔除。
边栏推荐
- Always of SystemVerilog usage_ comb 、always_ iff
- DVWA (5th week)
- JDBC transactions, batch processing, and connection pooling (super detailed)
- HackMyvm靶机系列(5)-warez
- Network layer - simple ARP disconnection
- MSF generate payload Encyclopedia
- [VMware abnormal problems] problem analysis & Solutions
- Interpretation of iterator related "itertools" module usage
- "Gold, silver and four" job hopping needs to be cautious. Can an article solve the interview?
- Harmonyos JS demo application development
猜你喜欢
HackMyvm靶机系列(6)-videoclub
Network layer - simple ARP disconnection
SRC mining ideas and methods
Wei Shen of Peking University revealed the current situation: his class is not very good, and there are only 5 or 6 middle-term students left after leaving class
Record once, modify password logic vulnerability actual combat

强化學習基礎記錄
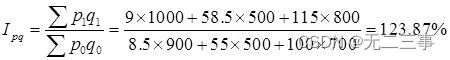
《统计学》第八版贾俊平第十四章指数知识点总结及课后习题答案
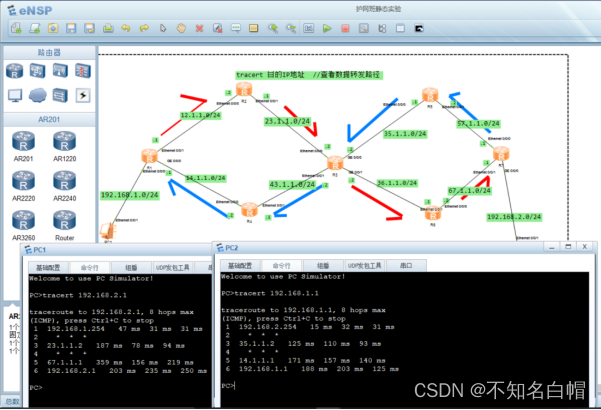
Detailed explanation of network foundation routing
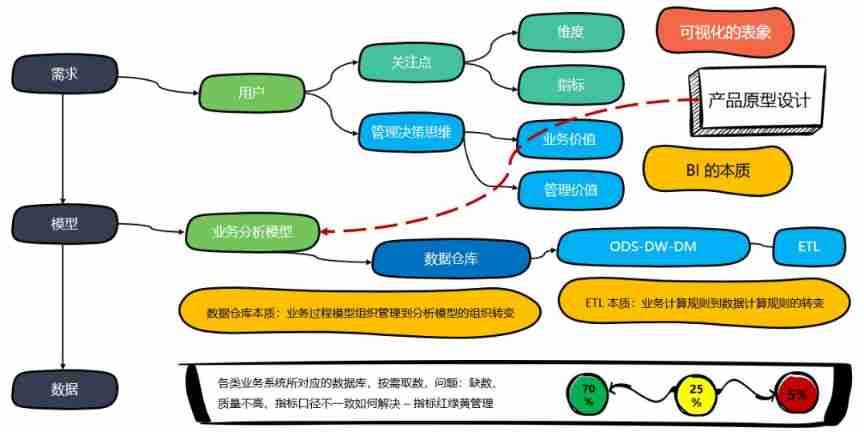
How to understand the difference between technical thinking and business thinking in Bi?
![[paper reproduction] cyclegan (based on pytorch framework) {unfinished}](/img/16/43d8929d1a37c1c68e959d5854e18c.jpg)
[paper reproduction] cyclegan (based on pytorch framework) {unfinished}
随机推荐
Sqqyw (indifferent dot icon system) vulnerability recurrence and 74cms vulnerability recurrence
How to test whether an object is a proxy- How to test if an object is a Proxy?
Meituan dynamic thread pool practice ideas, open source
Matlab opens M file garbled solution
JDBC事务、批处理以及连接池(超详细)
Circular queue (C language)
Harmonyos application development -- address book management system telmanagesys based on listcontainer [phonebook][api v6]
Load balancing ribbon of microservices
Captcha killer verification code identification plug-in
What language should I learn from zero foundation. Suggestions
外网打点(信息收集)
Simply understand the promise of ES6
【数据库 三大范式】一看就懂
Intranet information collection of Intranet penetration (4)
The difference between layer 3 switch and router
循环队列(C语言)
Intranet information collection of Intranet penetration (5)
《统计学》第八版贾俊平第十三章时间序列分析和预测知识点总结及课后习题答案
搭建域环境(win)
【educoder数据库实验 索引】