当前位置:网站首页>《统计学》第八版贾俊平第七章知识点总结及课后习题答案
《统计学》第八版贾俊平第七章知识点总结及课后习题答案
2022-07-06 09:23:00 【无二三事】
一.考点归纳

参数估计的基本原理
1置信区间
(1)置信水平为95%的置信区间的含义:用某种方法构造的所有区间中有95%的区间包含总体参数的真值。(2)置信度愈高(即估计的可靠性愈高),则置信区间相应也愈宽(即估计准确性愈低)。
(3)置信区间的特点:置信区间受样本影响,具有随机性,总体参数的真值是固定的。一个特定的置信区间“总是包含”或“绝对不包含”参数的真值,不存在“以多大的概率包含总体参数”的问题。
2评价估计量的标准
(1)无偏性:估计量抽样分布的期望值等于被估计的总体参数,即E(θ)=θ。
(2)有效性:估计量的方差尽可能小。
(3)一致性:随着样本量的增大,估计量的值越来越接近被估计总体的参数。
一个总体参数的区间估计


二、课后习题及答案
1利用下面的信息,构建总体均值的置信区间。
(1)总体服从正态分布,且已知σ=500,n=15,x=8900,置信水平为95%。
(2)总体不服从正态分布,且已知σ=500,n=35,x=8900,置信水平为95%。
(3)总体不服从正态分布,σ未知,n=35,x=8900,s=500,置信水平为90%。
(4)总体不服从正态分布,σ未知,n=35,x=8900,s=500,置信水平为99%。
解:(1)由于总体服从正态分布,σ=500,n=15,x=8900,α=0.05,z0.05/2=1.96。所以总体均值μ的95%的置信区间为:
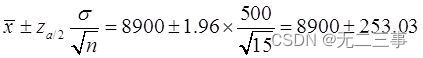
即(8646.97,9153.03)。
(2)已知总体不服从正态分布,但n=35为大样本,因此采用z统计量,总体均值μ的95%的置信区间为:
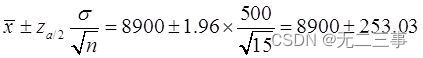
即(8734.35,9065.65)。
(3)已知总体不服从正态分布,σ未知,但由于n=35为大样本,因此可以采用z统计量,总体均值μ的90%的置信区间为:
即(8760.97,9039.03)。
(4)已知总体不服从正态分布,σ未知,但由于n=35为大样本,因此可以采用z统计量,总体均值μ的99%的置信区间为:
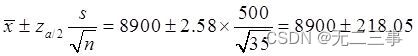
即(8681.95,9118.05)。
2某大学为了解学生每天上网的时间,在全校7500名学生中采取重复抽样方法随机抽取36人,调查他们每天上网的时间,得到表7-3的数据(单位:小时)。
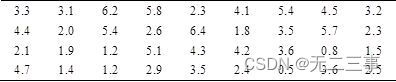
求该校大学生平均上网时间的置信区间,置信水平分别为90%,95%和99%。
解:已知:n=36,当α为0.1,0.05,0.01时,相应的z值分别为:z0.1/2=1.645,z0.05/2=1.96,z0.01/2=2.58
根据样本数据计算得:
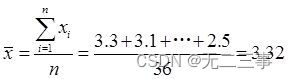
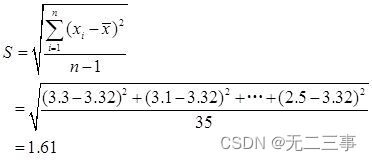
(1)由于n=36为大样本,所以平均上网时间的90%的置信区间为:
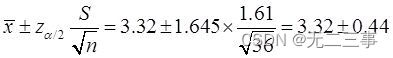
即(2.88,3.76)。
(2)平均上网时间的95%的置信区间为:
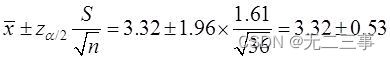
即(2.79,3.85)。
(3)平均上网时间的99%的置信区间为:
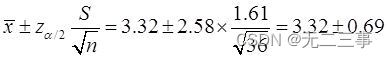
即(2.63,4.01)。
3某企业生产的袋装食品采用自动打包机包装,每袋标准重量为100g,现从某天生产的一批产品中按重复抽样随机抽取50包进行检查,测得每包重量如表所示。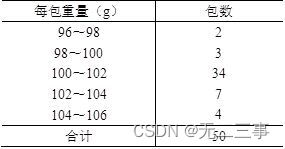
已知食品包重量从正态分布,要求:
(1)确定该种食品平均重量的95%的置信区间。
(2)如果规定食品重量低于100g属于不合格,确定该批食品合格率的95%的置信区间。
解:(1)已知:总体服从正态分布,但σ未知,n=50为大样本,α=0.05,z0.05/2=1.96。根据分组的样本数据计算得:x=(97×2+99×3+…+105×4)/50=101.32
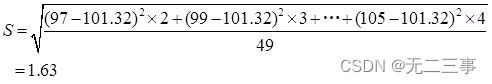
该种食品平均重量的95%的置信区间为:
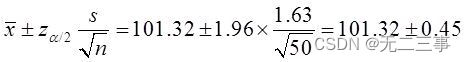
即(100.87,101.77)。
(2)根据样本数据可知,样本合格率为p=45/50=0.9。该种食品合格率的95%的置信区间为:
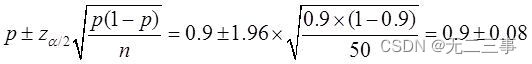
即(0.82,0.98)。
4假设总体服从正态分布,利用表7-5的数据构建总体均值μ的99%的置信区间。

解:已知:总体服从正态分布,但σ未知,n=25为小样本,α=0.01,t0.01/2(25-1)=2.797。根据样本数据计算得:x=16.128,s=0.871。则总体均值μ的99%的置信区间为:
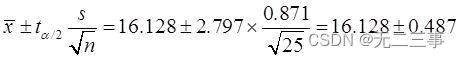
即(15.64,16.62)。
5利用下面的样本数据构建总体比例π的置信区间。
(1)n=44,p=0.51,置信水平为99%。
(2)n=300,p=0.82,置信水平为95%。
(3)n=1150,p=0.48,置信水平为90%。
解:(1)已知:n=44,p=0.51,α=0.01,z0.01/2=2.58。总体比例π的99%的置信区间为:
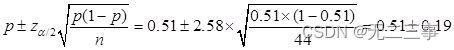
即(0.32,0.70)。
(2)已知:n=300,p=0.82,α=0.05,z0.05/2=1.96。总体比例π的95%的置信区间为:
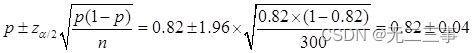
即(0.78,0.86)。
(3)已知:n=1150,p=0.48,α=0.1,z0.1/2=1.645。总体比例π的90%的置信区间为:
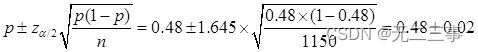
即(0.46,0.50)。
6在一项家电市场调查中,随机抽取了200个居民户,调查他们是否拥有某一品牌的电视机。其中拥有该品牌电视机的家庭占23%。求总体比例的置信区间,置信水平分别为90%和95%。解:已知:n=200,p=0.23,α为0.1和0.05时,相应的z0.1/2=1.645,z0.05/2=1.96。
(1)总体比例π的90%的置信区间为:
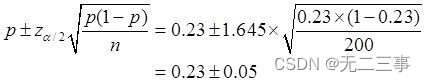
即(0.18,0.28)。
(2)总体比例π的95%的置信区间为:
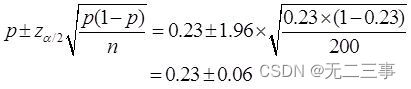
即(0.17,0.29)。
7一位银行的管理人员想估计每位顾客在该银行的月平均存款额。他假设所有顾客月存款额的标准差为1000元,要求的估计误差在200元以内。置信水平为99%,应选取多大的样本?解:已知:σ=1000,估计误差E=200,α=0.01,z0.01/2=2.58。所以应抽取的样本量为:
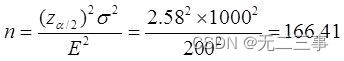
所以应抽取167个样本。
8某居民小区共有居民500户,小区管理者准备采用一种新的供水设施,想了解居民是否赞成。采取重复抽样方法随机抽取了50户,其中有32户赞成,18户反对。
(1)求总体中赞成该项改革的户数比例的置信区间(α=0.05)。
(2)如果小区管理者预计赞成的比例能达到80%,估计误差不超过10%。应抽取多少户进行调查(α=0.05)?
解:(1)已知:n=50,p=32/50=0.64,α=0.05,z0.05/2=1.96。总体中赞成该项改革的户数比例的95%的置信区间为:
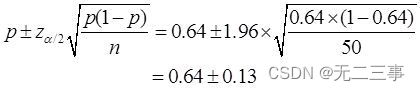
即(0.51,0.77)。
(2)已知:π=0.80,α=0.05,z0.05/2=1.96。应抽取的样本量为:
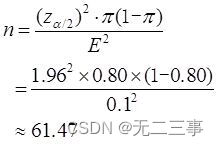
即应抽取的样本量为62户。
9根据下面的样本结果,计算总体标准差σ的90%的置信区间。
(1)x=21,s=2,n=50。
(2)x=1.3,s=0.02,n=15。
(3)x=167,s=31,n=22。
解:(1)已知:x=21,s=2,n=50,α=0.1,查表得:χ20.1/2(50-1)=66.3387,χ21-0.1/2(50-1)=33.9303。总体方差σ2的置信区间为:
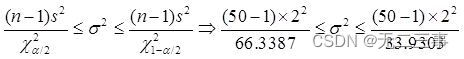
即2.95≤σ2≤5.78。标准差的置信区间为:1.72≤σ≤2.40。
(2)已知:x=1.3,s=0.02,n=15,α=0.1,查表得:χ20.1/2(15-1)=23.6848,χ21-0.1/2(15-1)=6.5706。总体方差σ2的置信区间为:
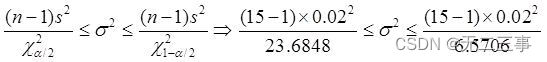
标准差的置信区间为:0.015≤σ≤0.029。
(3)已知:x=167,s=31,n=22,α=0.1,查表得:χ20.1/2(22-1)=32.6706,χ21-0.1/2(22-1)=11.5913。总体方差σ2的置信区间为:
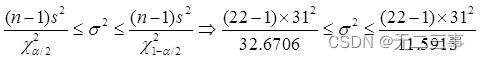
标准差的置信区间为:24.85≤σ≤41.73。
10顾客到银行办理业务时往往需要等待一段时间,而等待时间的长短与许多因素有关。比如,银行业务员办理业务的速度,顾客等待排队的方式等。为此,某银行准备采取两种排队方式进行试验,第一种排队方式是:所有顾客都进入一个等待队列;第二种排队方式是:顾客在三个业务窗口处列队三排等待。为比较哪种排队方式使顾客等待的时间更短,银行各随机抽取10名顾客,他们在办理业务时所等待的时间(单位:分钟),如表所示。![]()
要求:
(1)构建第一种排队方式等待时间标准差的95%的置信区间。
(2)构建第二种排队方式等待时间标准差的95%的置信区间。
(3)根据(1)和(2)的结果,你认为哪种排队方式更好?
解:(1)已知:n=10,α=0.05,查表得χ0.05/22(10-1)=19.0228,χ1-0.05/22(10-1)=2.7004。根据方式1的样本数据计算得:s2=0.2272。总体方差σ2的置信区间为:
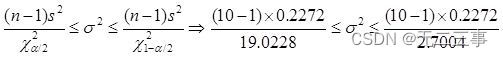
标准差的置信区间为:0.33≤σ≤0.87。
(2)根据方式2的样本数据计算得:s2=3.3183。总体方差σ2的置信区间为:
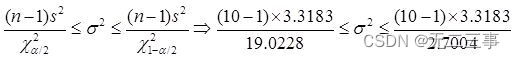
标准差的置信区间为:1.25≤σ≤3.33。
(3)第一种排队方式更好,因为它的离散程度小于第二种排队方式。
11从两个正态总体中分别抽取两个独立的随机样本,它们的均值和标准差如表所示。
(1)设n1=n2=100,求(μ1-μ2)95%的置信区间。
(2)设n1=n2=10,σ12=σ22,求(μ1-μ2)95%的置信区间。
(3)设n1=n2=10,σ12≠σ22,求(μ1-μ2)95%的置信区间。
(4)设n1=10,n2=20,σ12=σ22,求(μ1-μ2)95%的置信区间。
(5)设n1=10,n2=20,σ12≠σ22,求(μ1-μ2)95%的置信区间。
解:(1)由于两个样本均为独立大样本,σ12和σ22未知。当α=0.05时,z0.05/2=1.96,则μ1-μ2的95%的置信区间为:
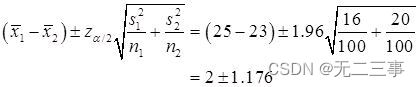
即(0.824,3.176)。
(2)由于两个样本均为来自正态总体的独立小样本,当σ12和σ22未知但σ12=σ22时,需要用两个样本的方差s12和s22和来估计。总体方差的合并估计量sp2为:

当α=0.05时,t0.05/2(10+10-2)=2.101,则μ1-μ2的95%的置信区间为:
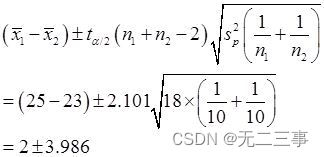
即(-1.986,5.986)。
(3)由于两个样本均为来自正态总体的独立小样本,σ12和σ22未知且σ12≠σ22,n1=n2=n。当α=0.05时,t0.05/2(10+10-2)=2.101,则μ1-μ2的95%的置信区间为:

即(-1.986,5.986)。
(4)由于两个样本均为来自正态总体的独立小样本,σ12和σ22未知但σ12=σ22,n1≠n2。需要用两个样本的方差s12和s22来估计。总体方差的合并估计量sp2为:
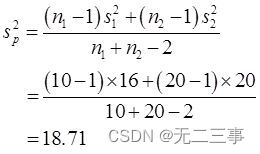
当α=0.05时,t0.05/2(10+20-2)=2.048。因此,μ1-μ2的95%的置信区间为:
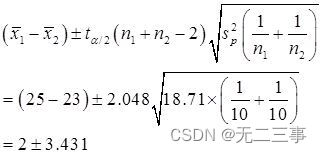
即(-1.431,5.431)。
(5)由于两个样本均为来自正态总体的独立小样本,σ12和σ22未知且σ12≠σ22,n1≠n2。因此,μ1-μ2的95%的置信区间为:
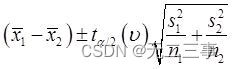
自由度的计算如下:
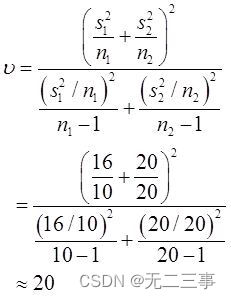
当α=0.05时,t0.05/2(20)=2.086。μ1-μ2的95%的置信区间为:
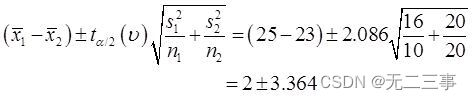
即(—1.364,5.364)。
12表7-8是由4对观察值组成的随机样本。
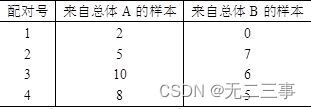
(1)计算A与B各对观察值之差,再利用得出的差值计算d和sd。
(2)设μ1和μ2分别为总体A和总体B的均值,构造μd=μ1-μ2的95%的置信区间。
解:(1)计算过程如表7-9所示。
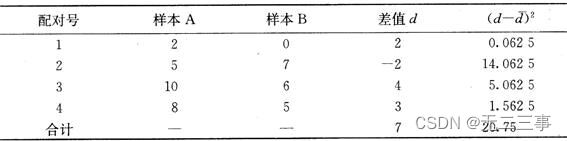
d=7/4=1.75
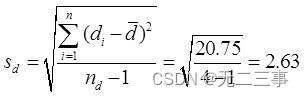
(2)当α=0.05时,t0.05/2(4-1)=3.182。两个样本之差μd=μ1-μ2的95%的置信区间为:
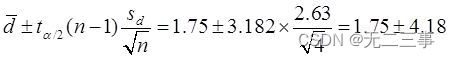
即(-2.43,5.93)。
13一家人才测评机构对随机抽取的10名小企业的经理人用两种方法进行自信心测试,得到的自信心测试分数如表7-10所示。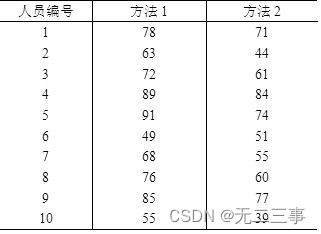
要求:构建两种方法平均自信心得分之差μd=μ1-μ2的95%的置信区间。
解:根据样本数据计算得:d=[(78-71)+(63-44)+…+(55-39)]/10=110/10=11
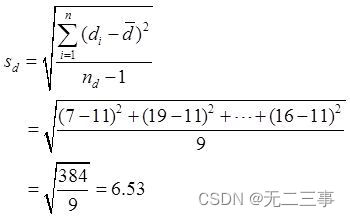
当α=0.05时,t0.05/2(10-1)=2.262。两种方法平均自信心得分之差μd=μ1-μ2的95%的置信区间为:
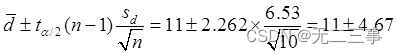
即(6.33,15.67)。
14从两个总体中各抽取一个n1=n2=250的独立随机样本,来自总体1的样本比例为p1=40%,来自总体2的样本比例为p2=30%。要求:
(1)构造π1-π2的90%的置信区间。
(2)构造π1-π2的95%的置信区间。
解:(1)已知:n1=n2=250,p1=40%,p2=30%,α=0.1,z0.1/2=1.645。π1-π2的90%的置信区间为:
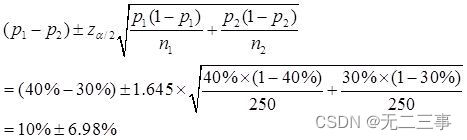
即(3.02%,16.98%)。
(2)α=0.05,z0.05/2=1.96。π1-π2的90%的置信区间为:
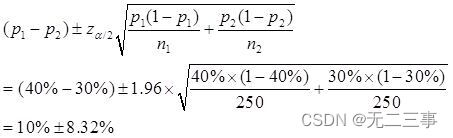
即(1.68%,18.32%)。
15生产工序的方差是工序质量的一个重要度量。当方差较大时,需要对工序进行改进以减小方差。表7-11是两部机器生产的袋茶重量(单位:g)的数据。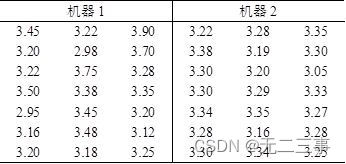
要求:构造两个总体方差比(σ12/σ22)95%的置信区间。解:根据样本数据计算得:s12=0.058375,s22=0.005846。当α=0.05时,由Exce1的“FINV”函数计算得:F0.025(21-1,21-1)=2.46,F1-α/2(n1-1,n2-1)=F0.975(21-1,21-1)=0.41。两个总体方差比σ12/σ22的95%的置信区间为:
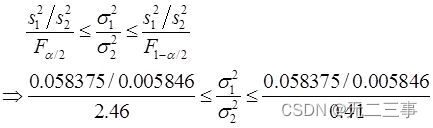
即两个总体方差比σ12/σ22的95%的置信区间为:4.06≤σ12/σ22≤24.35。
16根据以往的生产数据,某种产品的废品率为2%。如果置信区间为95%,估计误差不超过4%,应抽取多少样本?解:已知:π=2%,E=4%,当α=0.05时,z0.05/2=1.96。应抽取的样本量为:
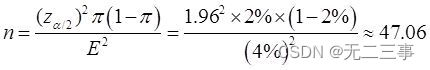
故应至少抽取样本量为48的样本。
边栏推荐
- Hackmyvm target series (1) -webmaster
- Meituan dynamic thread pool practice ideas, open source
- Load balancing ribbon of microservices
- 内网渗透之内网信息收集(一)
- 记一次edu,SQL注入实战
- Constants, variables, and operators of SystemVerilog usage
- Experiment 8 exception handling
- Web vulnerability - File Inclusion Vulnerability of file operation
- 7-3 construction hash table (PTA program design)
- MySQL interview questions (4)
猜你喜欢
![[VMware abnormal problems] problem analysis & Solutions](/img/64/f44864da600b61a1a646a5865a2083.jpg)
[VMware abnormal problems] problem analysis & Solutions
Record an API interface SQL injection practice
On the idea of vulnerability discovery
Based on authorized access, cross host, and permission allocation under sqlserver
HackMyvm靶机系列(6)-videoclub

Intranet information collection of Intranet penetration (5)

浅谈漏洞发现思路
记一次edu,SQL注入实战
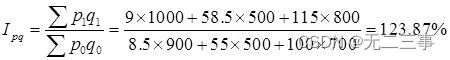
《统计学》第八版贾俊平第十四章指数知识点总结及课后习题答案
链队实现(C语言)
随机推荐
DVWA (5th week)
Load balancing ribbon of microservices
Network technology related topics
7-14 error ticket (PTA program design)
【educoder数据库实验 索引】
记一次,修改密码逻辑漏洞实战
HackMyvm靶機系列(3)-visions
7-5 staircase upgrade (PTA program design)
Experiment 8 exception handling
Attack and defense world misc practice area (simplerar, base64stego, no matter how high your Kung Fu is, you are afraid of kitchen knives)
Strengthen basic learning records
内网渗透之内网信息收集(二)
Record an API interface SQL injection practice
Sqqyw (indifferent dot icon system) vulnerability recurrence and 74cms vulnerability recurrence
Intranet information collection of Intranet penetration (I)
Hackmyvm Target Series (3) - vues
[experiment index of educator database]
List and data frame of R language experiment III
Experiment 4 array
Harmonyos application development -- address book management system telmanagesys based on listcontainer [phonebook][api v6]