当前位置:网站首页>Several methods of image enhancement and matlab code
Several methods of image enhancement and matlab code
2022-07-02 07:58:00 【MezereonXP】
1. Gray linear transformation
Gray linear transformation , It is a method of airspace , Directly operate the gray value of each pixel
Suppose the image is I I I
Then the gray value of each pixel is I ( x , y ) I(x,y) I(x,y)
We can get :
I ( x , y ) ∗ = k ∗ I ( x , y ) + b I(x,y)^*=k*I(x,y)+b I(x,y)∗=k∗I(x,y)+b
take k = 1 , b = 16 k=1,b=16 k=1,b=16 You can get



Here are the key codes
original = imread(strcat(strcat('resource\',name),'.bmp'));
transformed = LinearFunction(original, 1, 16);
subplot(1,3,3);
imshow(transformed)
title(' Image after linear transformation ')
imwrite(transformed,strcat(strcat('result\',name),'(linear).jpg'))
2. Histogram equalization transform
This method is usually used to increase the global contrast of many images , Especially when the contrast of the useful data of the image is quite close . In this way , Brightness can be better distributed on histogram . This can be used to enhance the local contrast without affecting the overall contrast , Histogram equalization can achieve this function by effectively expanding the commonly used brightness .
This method is very useful for both background and foreground images that are too bright or too dark , This method, in particular, can bring about X Better display of bone structure in light images and better details in overexposed or underexposed photos . One of the main advantages of this method is that it is a fairly intuitive technology and reversible operation , If the equalization function is known , Then we can restore the original histogram , And the amount of calculation is not big . One disadvantage of this method is that it does not select the data to be processed , It may increase the contrast of background noise and decrease the contrast of useful signals .
Consider a discrete grayscale image { x } \{x\} { x}
Give Way n i n_i ni Indicates grayscale i i i Number of occurrences , So the grayscale of the image is i i i The probability of pixels appearing is :
p x ( i ) = p ( x = i ) = n i n , 0 ≤ i < L p_x(i)=p(x=i)=\frac{n_i}{n}, 0\leq i<L px(i)=p(x=i)=nni,0≤i<L
L L L Is the number of grayscale in the image ( Usually 255)
Corresponding to p x p_x px The cumulative distribution function of , Defined as :
c d f x ( i ) = ∑ j = 0 i p x ( j ) cdf_x(i)=\sum_{j=0}^i{p_x(j)} cdfx(i)=∑j=0ipx(j)
Is the cumulative normalized histogram of the image
We create a form of y = T ( x ) y=T(x) y=T(x) Transformation of , For each value of the original image, it generates a y y y, such y y y The cumulative probability function of can be linearized in all value ranges , The conversion formula is defined as :
c d f y ( i ) = i K cdf_y(i)=iK cdfy(i)=iK
For constants K, C D F CDF CDF The nature of allows us to make such transformations , Defined as :
c d f y ( y ′ ) = c d f y ( T ( k ) ) = c d f x ( k ) cdf_y(y')=cdf_y(T(k))=cdf_x(k) cdfy(y′)=cdfy(T(k))=cdfx(k)
among k ∈ [ 0 , L ) k\in [0,L) k∈[0,L), Be careful T T T Map different gray levels to ( 0 , 1 ) (0,1) (0,1), To map these values to the original domain , You need to apply the following simple transformation to the result :
y ′ = y ∗ ( m a x { x } − m i n { x } ) + m i n { x } y' = y*(max\{x\}-min\{x\})+min\{x\} y′=y∗(max{ x}−min{ x})+min{ x}
Give some results :



Give the key code :
m = 255;
subplot(1,3,3);
H = histeq(I,m);
imshow(H,[]);
title(‘ Image after histogram equalization ’);
Similarly , We can rgb Image histogram equalization , Here is the result



[M,N,G]=size(I1);
result=zeros(M,N,3);
% Get every point of every layer RGB value , And determine its value
for g=1:3
A=zeros(1,256);
% After each layer , The parameter should be reinitialized to 0
average=0;
for k=1:256
count=0;
for i=1:M
for j=1:N
value=I1(i,j,g);
if value==k
count=count+1;
end
end
end
count=count/(M*N*1.0);
average=average+count;
A(k)=average;
end
A=uint8(255.*A+0.5);
for i=1:M
for j=1:N
I1(i,j,g)=A(I1(i,j,g)+0.5);
end
end
end
% Show the treatment effect
subplot(1,3,3);
imshow(I1);
3. Homomorphic filtering
Homomorphic filtering is used to remove Multiplicative noise (multiplicative noise), It can increase contrast and standardize brightness at the same time , So as to achieve the purpose of image enhancement .
An image can be represented as its Intensity of illumination (illumination) Weight and Reflection (reflectance) The product of components , Although the two are inseparable in the time domain , But through Fourier transform, the two can be linearly separated in the frequency domain . Since the illuminance can be regarded as the lighting in the environment , The relative change is very small , It can be regarded as the low-frequency component of the image ; The reflectivity changes relatively large , It can be regarded as a high-frequency component . The influence of illuminance and reflectivity on pixel gray value is processed respectively , Usually by High pass filter (high-pass filter), Make the lighting of the image more uniform , Achieve the purpose of enhancing the detailed features of the shadow area .
It is :
For an image , It can be expressed as the product of illumination component and reflection component , That is to say :
m ( x , y ) = i ( x , y ) ⋅ r ( x , y ) m(x,y)=i(x,y)\cdot r(x,y) m(x,y)=i(x,y)⋅r(x,y)
among , m m m It's an image , i i i Is the illuminance component , r r r Is the reflection component
In order to use high pass filter in frequency domain , We have to do Fourier transform , But because the above formula is a product , It is not possible to directly operate the illumination component and reflection component , So take the logarithm of the above formula
l n ( m ( x , y ) ) = l n ( i ( x , y ) ) + l n ( r ( x , y ) ) ln(m(x,y))=ln(i(x,y))+ln(r(x,y)) ln(m(x,y))=ln(i(x,y))+ln(r(x,y))
Then Fourier transform the above formula
F { l n ( m ( x , y ) ) } = F { l n ( i ( x , y ) ) } + F { l n ( r ( x , y ) ) } \mathcal{F}\{ln(m(x,y))\}=\mathcal{F} \{ ln(i(x,y))\}+ \mathcal{F}\{ln(r(x,y))\} F{ ln(m(x,y))}=F{ ln(i(x,y))}+F{ ln(r(x,y))}
We will F { l n ( m ( x , y ) ) } \mathcal{F}\{ln(m(x,y))\} F{ ln(m(x,y))} Defined as M ( u , v ) M(u,v) M(u,v)
Next, high pass filter the image , In this way, the illumination of the image can be more uniform , The high-frequency component increases and the low-frequency component decreases
N ( u , v ) = H ( u , v ) ⋅ M ( u , v ) N(u,v)=H(u,v)\cdot M(u,v) N(u,v)=H(u,v)⋅M(u,v)
among H H H It's a high pass filter
In order to transfer the image from the frequency domain back to the time domain , We are right. N N N Do inverse Fourier transform
n ( x , y ) = F − 1 { N ( x , y ) } n(x,y)=\mathcal{F}^{-1}\{N(x,y)\} n(x,y)=F−1{ N(x,y)}
Finally, use the exponential function to restore the logarithm we took at the beginning
m ′ ( x , y ) = e x p { n ( x , y ) } m'(x,y)=exp\{n(x,y)\} m′(x,y)=exp{ n(x,y)}
The results are given



Give some key codes
I=double(I);
[M,N]=size(I);
rL=0.5;
rH=4.7;% The parameters can be adjusted according to the desired effect
c=2;
d0=10;
I1=log(I+1);% Take the logarithm
FI=fft2(I1);% The Fourier transform
n1=floor(M/2);
n2=floor(N/2);
H = ones(M, N);
for i=1:M
for j=1:N
D(i,j)=((i-n1).^2+(j-n2).^2);
H(i,j)=(rH-rL).*(exp(c*(-D(i,j)./(d0^2))))+rL;% Gaussian homomorphic filtering
end
end
I2=ifft2(H.*FI);% Inverse Fourier transform
I3=real(exp(I2));
subplot(1,3,3),imshow(I3,[]);title(' After homomorphic filtering is enhanced ');
边栏推荐
- 【FastDepth】《FastDepth:Fast Monocular Depth Estimation on Embedded Systems》
- Programmers can only be 35? The 74 year old programmer in the United States has been programming for 57 years and has not retired
- 业务架构图
- In the era of short video, how to ensure that works are more popular?
- Target detection for long tail distribution -- balanced group softmax
- 针对语义分割的真实世界的对抗样本攻击
- TimeCLR: A self-supervised contrastive learning framework for univariate time series representation
- 【Programming】
- [mixup] mixup: Beyond Imperial Risk Minimization
- WCF更新服务引用报错的原因之一
猜你喜欢

【DIoU】《Distance-IoU Loss:Faster and Better Learning for Bounding Box Regression》

【Sparse-to-Dense】《Sparse-to-Dense:Depth Prediction from Sparse Depth Samples and a Single Image》
服务器的内网可以访问,外网却不能访问的问题
Thesis writing tip2

MoCO ——Momentum Contrast for Unsupervised Visual Representation Learning
Hystrix dashboard cannot find hystrix Stream solution
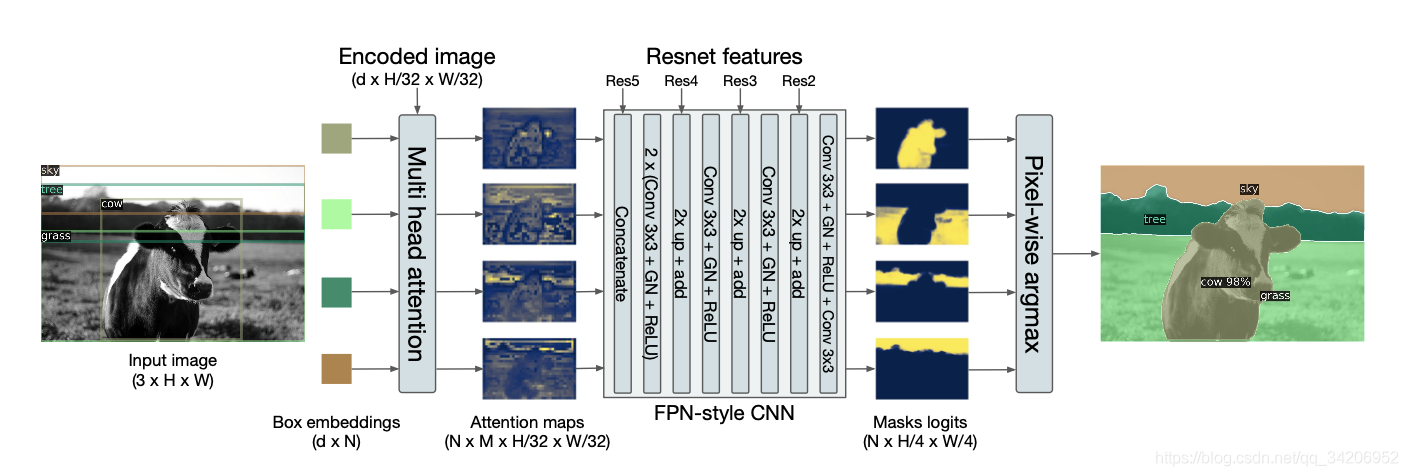
利用Transformer来进行目标检测和语义分割

半监督之mixmatch
![[learning notes] numerical differentiation of back error propagation](/img/1c/e28e31d7cc5ccc38607c7839ccc5f0.png)
[learning notes] numerical differentiation of back error propagation

【FastDepth】《FastDepth:Fast Monocular Depth Estimation on Embedded Systems》
随机推荐
[Sparse to Dense] Sparse to Dense: Depth Prediction from Sparse Depth samples and a Single Image
Summary of open3d environment errors
w10升级至W11系统,黑屏但鼠标与桌面快捷方式能用,如何解决
Income in the first month of naked resignation
(15) Flick custom source
Common machine learning related evaluation indicators
浅谈深度学习中的对抗样本及其生成方法
C#与MySQL数据库连接
[in depth learning series (8)]: principles of transform and actual combat
半监督之mixmatch
Vscode下中文乱码问题
Jetson nano installation tensorflow stepping pit record (scipy1.4.1)
[C # note] the data in DataGridView saved in WinForm is excel and CSV
Gensim如何冻结某些词向量进行增量训练
[learning notes] matlab self compiled Gaussian smoother +sobel operator derivation
【Programming】
【FastDepth】《FastDepth:Fast Monocular Depth Estimation on Embedded Systems》
【TCDCN】《Facial landmark detection by deep multi-task learning》
E-R draw clear content
Handwritten call, apply, bind