当前位置:网站首页>Machine learning -- decision tree (sklearn)
Machine learning -- decision tree (sklearn)
2022-07-06 11:53:00 【Want to be a kite】
machine learning – Decision tree (sklearn)
Decision tree is a basic machine learning method of classification and regression based on tree structure . Decision tree consists of nodes and directed edges , Nodes are divided into internal nodes ( Represent the division of a feature ) And leaf nodes ( Represents a category or output ).
Decision tree learning , Training data set
𝐷 = ( 𝐱 1 , 𝑦 1 ) , ( 𝐱 2 , 𝑦 2 ) , ⋯ , ( 𝐱 𝑖 , 𝑦 𝑖 ) , ⋯ , ( 𝐱 𝑁 , 𝑦 𝑁 ) 𝐷 = {(𝐱1, 𝑦1) , (𝐱2, 𝑦2) , ⋯ , (𝐱𝑖, 𝑦𝑖) , ⋯ , (𝐱𝑁, 𝑦𝑁)} D=(x1,y1),(x2,y2),⋯,(xi,yi),⋯,(xN,yN)
among , x i xi xi For the first time eigenvectors ( example ),
𝐱 𝑖 = ( 𝑥 ( 𝑖 1 ) , 𝑥 ( 𝑖 2 ) , … , 𝑥 ( 𝑖 𝑗 ) , … , 𝑥 ( 𝑖 𝑛 ) ) 𝑇 𝐱𝑖 = (𝑥( 𝑖1), 𝑥( 𝑖2), … , 𝑥( 𝑖𝑗), … , 𝑥( 𝑖𝑛))^𝑇 xi=(x(i1),x(i2),…,x(ij),…,x(in))T , y i yi yi by x i xi xi Category tags for ,
𝑦 𝑖 ∈ 1 , 2 , ⋯ , 𝐾 𝑦𝑖 ∈ {1, 2, ⋯ , 𝐾} yi∈1,2,⋯,K.
Study of the ⽬ The standard number is constructed according to the given training data set ⼀ Decision tree models , Make it possible to enter ⾏ Correct Classification or regression .
Decision tree learning includes 3 A step : feature selection 、 Decision tree ⽣ become 、 Pruning decision tree .
One 、 feature selection
Feature selection is to select features with classification ability for training data .
The measurement of uncertainty in entropy representation of random variables .( More detailed conceptual understanding , Consult information theory 、 Fundamentals of communication principles .)
set up X X X Is a discrete random variable with finite values , The probability distribution is
P ( X = x i ) = p i , i = 1 , 2 , , . . . , n P(X=xi)=pi,i=1,2,,...,n P(X=xi)=pi,i=1,2,,...,n
Then the random variable X X X The entropy of
H ( X ) = H ( p ) = − ∑ p i l o g 𝑝 𝑖 H(X)=H(p)= − ∑pi log 𝑝𝑖 H(X)=H(p)=−∑pilogpi
H ( p ) H(p) H(p) Value range of : 0 < H ( p ) < l o g n 0<H(p)<log n 0<H(p)<logn, When p = 0.5 p=0.5 p=0.5 when , Get the maximum .
The information gain algorithm is shown in the figure below :
Take the information gain as the feature, and select the feature with more standard values . When there are many values of features , According to this feature, it is easier to obtain higher purity subsets , Therefore, the entropy after division is lower . Because the entropy before partition is certain , Therefore, the information gain is greater .
Two 、 Decision tree generation
ID3 Algorithm :
Input : Training data set D D D, Feature set A A A, threshold ϵ \epsilon ϵ
Output : Decision tree T T T
C4.5 Algorithm :
Input : Training data set D D D, Feature set A A A, threshold ϵ \epsilon ϵ
Output : Decision tree T T T
3、 ... and 、 Decision tree pruning
Pruning of decision tree is realized by minimizing the overall loss function or cost function of decision tree .
Set tree T T T The number of leaf nodes is | T T T|, t t t It's a tree. T T T Leaf node of , The leaf node has N t N_t Nt individual , k = 1 , 2 , . . . , K k=1,2,...,K k=1,2,...,K,
H t ( T ) H_t(T) Ht(T) For leaf nodes t t t Empirical entropy on , Then the loss function of the decision tree :
among , C ( T ) C(T) C(T) Represents the prediction error of the model to the training data , That is, the fitting degree of the model and the training data , ∣ T ∣ |T| ∣T∣ Represents the complexity of the model , Parameters α > = 0 α>=0 α>=0 Control the impact between the two .
Tree pruning algorithm :
Input : Decision tree T T T, Parameters α α α
Output : The sub tree after construction T α T_α Tα
- Calculate the empirical entropy of each node
- Recursively retract from the leaf node of the tree . Let a group of leaf nodes retract to the whole tree before and after its parent node as T B And T A T_B And T_A TB And TA, Their loss function values for are C α ( T B ) And C α ( T A ) C_α(T_B) And C_α(T_A) Cα(TB) And Cα(TA), If C α ( T A ) < = C α ( T B ) C_α(T_A) <= C_α(T_B) Cα(TA)<=Cα(TB). Then prune , That is, the parent node becomes a new leaf node .
- return 2., Until we can't continue , Get the subtree with the smallest loss function T α T_α Tα.
Four 、 Classification and regression trees CART
4.1 The formation of regression trees

4.2 The generation of the classification tree

4.3CART Tree pruning
For whole tree T 0 T_0 T0 Any internal node t t t, With t t t Is the loss function of a single node tree
C α ( t ) = C ( t ) + α C_α(t) = C(t)+α Cα(t)=C(t)+α
With t t t Is the subtree of the root node T t T_t Tt Loss function of
C α ( T t ) = C ( T t ) + α ∣ T t ∣ C_α(T_t) = C(T_t)+α|T_t| Cα(Tt)=C(Tt)+α∣Tt∣
Implementation of decision tree -sklearn Library call mode and parameter interpretation
Decision tree ( Classification tree )
from sklearn.tree import DecisionTreeClassifier
DecisionTreeClassifier(criterion='gini',splitter='best',max_depth=None,
min_samples_split=2,min_samples_leaf=1,
min_weight_fraction_leaf=0.0,max_features=None,
random_state=None,max_leaf_nodes=None,
min_impurity_decrease=0.0,min_impurity_split=1e-07,
class_weight=None, presort=False)***
Parameters :
- criterion : A string , Specify the evaluation criteria for segmentation quality . It can be for
‘gini’ : Indicates that the segmentation standard is Gini coefficient . Select the attribute with small Gini coefficient for segmentation .
‘entropy’ : It means that the segmentation criterion is entropy . - splitter : A string , Specify the segmentation principle , It can be for :
best : Means to choose the best segmentation .
random : Indicates random segmentation .
default "best" Suitable for small sample size , And if the sample data volume is very large , At this point, the decision tree builds recommendations "random". - max_features : It can be an integer 、 floating-point 、 Characters or None, Specify to find best split The number of features considered .
If it's an integer , Then each segmentation only considers max_features Features .
If it's a floating point number , Every segmentation only considers max_features*n_features Features (max_features Specify percentage ).
If it's a string ‘auto’, be max_features be equal to n_features.
If it's a string ‘sqrt’, be max_features be equal to sqrt(n_features).
If it's a string ‘log2’, be max_features be equal to log2(n_features).
If it's a string None, be max_features be equal to n_features. - max_depth : It can be an integer or None, Specify the maximum depth of the tree , Prevent over fitting
If None, Indicates that the depth of the tree is unlimited ( Know that every leaf is pure , That is, all sample points in the leaf node belong to one class ,
Or the leaves contain less than min_sanples_split A sample points ).
If max_leaf_nodes The parameter is not None, Then ignore this item . - min_samples_split : Integers , Specify each internal node ( Nonleaf node ) The minimum number of samples included .
- min_samples_leaf : Integers , Specify the minimum number of samples contained in each leaf node .
- min_weight_fraction_leaf : Is a floating point number , The minimum weight coefficient of the sample in the leaf node .
- max_leaf_nodes : Is an integer or None, Specify the maximum number of leaf nodes .
If None, At this time, the number of leaf nodes is unlimited . If the None, be max_depth Be ignored . - min_impurity_decrease=0.0 If this split results in a reduction in impurity greater than or equal to this value , Then the node will be split .
- min_impurity_split=1e-07, Limit the growth of the decision tree ,
- class_weight : A dictionary 、 A list of dictionaries 、 character string ‘balanced’ perhaps None, He assigned the weight of the classification .
The weight form is :{class_label:weight} If None, Then the weight of each classification is 1.
character string ‘balanced’ The weight of each classification is the inverse ratio of the frequency of each classification in the sample . - random_state : An integer or a RandomState example , perhaps None.
If it's an integer , It specifies the seed of the random number generator .
If RandomState example , The random number generator is specified .
If None, Then use the default random number generator . - presort : A Boolean value , Specifies whether to sort the data in advance to speed up the process of finding the best segmentation .
Set to True when , For big data sets, slow down the overall training process , But for small data sets or when the maximum depth is set , Will accelerate the training process .
attribute :
- classes_ : The label value of the classification .
- feature_importances_ : The importance of the feature is given . The higher the value , The more important the feature is ( Also known as Gini importance).
- max_features_ : max_feature The inference of .
- n_classes_ : The number of classifications is given .
- n_features_ : When executed fit after , Number of features .
- n_outputs_ : When executed fit after , Number of outputs .
- tree_ : One Tree object , That is, the bottom decision tree .
Method : - fit(X,y) : Training models .
- predict(X) : Predict with a model , Return forecast .
- predict_log_proba(X) : Returns an array , The array elements are X The logarithm of the probability value predicted for each category .
- predict_proba(X) : Returns an array , The array elements are X Predict the probability of each category
- score(X,y) : Back in the (X,y) Accuracy of prediction on (accuracy).
Decision tree ( Back to the tree )
from sklearn.tree import DecisionTreeRegressor
DecisionTreeRegressor(criterion='mse',splitter='best',max_depth=None,min_samples
_split=2,min_samples_leaf=1,min_weight_fraction_leaf=0.0,max_features=None,rando
m_state=None,max_leaf_nodes=None,min_impurity_split=1e-07,presort=False)
Parameters :
- criterion : A string , Specify the evaluation criteria for segmentation quality . The default is ‘mse’, And only this string is supported , Mean square error .
- splitter : A string , Specify the segmentation principle , It can be for :best : Means to choose the best segmentation .random : Indicates random segmentation .
- max_features : It can be an integer 、 floating-point 、 Characters or None, Specify to find best split The number of features considered . If it's an integer , Then each segmentation only considers max_features Features . If it's a floating point number , Then each segmentation only considers max_features*n_features Features (max_features Percentage specified ).
If it's a string ‘auto’, be max_features be equal to n_features.
If it's a string ‘sqrt’, be max_features be equal to sqrt(n_features).
If it's a string ‘log2’, be max_features be equal to log2(n_features).
If it's a string None, be max_features be equal to n_features. - max_depth : It can be an integer or None, Specify the maximum depth of the tree .
If None, Indicates that the depth of the tree is unlimited ( Know that every leaf is pure , That is, all sample points in the leaf node belong to one class , Or the leaves contain less than min_sanples_split A sample points ). If max_leaf_nodes The parameter is not None, Then ignore this item . - min_samples_split : Integers , Specify each internal node ( Nonleaf node ) The minimum number of samples included .
- min_samples_leaf : Integers , Specify the minimum number of samples contained in each leaf node .
- min_weight_fraction_leaf : Is a floating point number , The minimum weight coefficient of the sample in the leaf node .
- max_leaf_nodes : Is an integer or None, Specify the maximum number of leaf nodes . If None, At this time, the number of leaf nodes is unlimited . If the None, be max_depth Be ignored .
- class_weight : A dictionary 、 A list of dictionaries 、 character string ‘balanced’ perhaps None, It specifies the weight of the classification . The weight form is :{class_label:weight} If None, Then the weight of each classification is 1. character string ‘balanced’ The weight of each classification is the inverse ratio of the frequency of each classification in the sample .
- random_state : An integer or a RandomState example , perhaps None. If it's an integer , It specifies the seed of the random number generator . If RandomState example , The random number generator is specified . If None, Then use the default random number generator .
- presort : A Boolean value , Specifies whether to sort the data in advance to speed up the process of finding the best segmentation .
Set to True when , For big data sets, slow down the overall training process , But for small data sets or when the maximum depth is set , Will accelerate the training process .
attribute :
- feature_importances_ : The importance of the feature is given . The higher the value , The more important the feature is ( Also known as Gini importance).
- max_features_ : max_feature The inference of .
- n_features_ : When executed fit after , Number of features .
- n_outputs_ : When executed fit after , Number of outputs .
- tree_ : One Tree object , That is, the bottom decision tree .
Method :
- fit(X,y) : Training models .
- predict(X) : Predict with a model , Return forecast .
- score(X,y) : Return the performance score
Iris classification ( Decision tree case , Call directly sklearn)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import graphviz
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def creat_data():
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100,[0,1,-1]])
return data[:,:2],data[:,-1]
X,y = creat_data()
X_train,X_test ,y_train,y_test = train_test_split(X,y)
clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
print(clf.score(X_test,y_test))
print(clf.feature_importances_) #k Check the importance of the feature
# Other properties can be viewed
tree_pic = export_graphviz(clf,out_file='Tree.pdf')
with open("Tree.pdf") as f:
dot_graph = f.read()
graphviz.Source(dot_graph)
You need to use graphviz. Installation is more troublesome !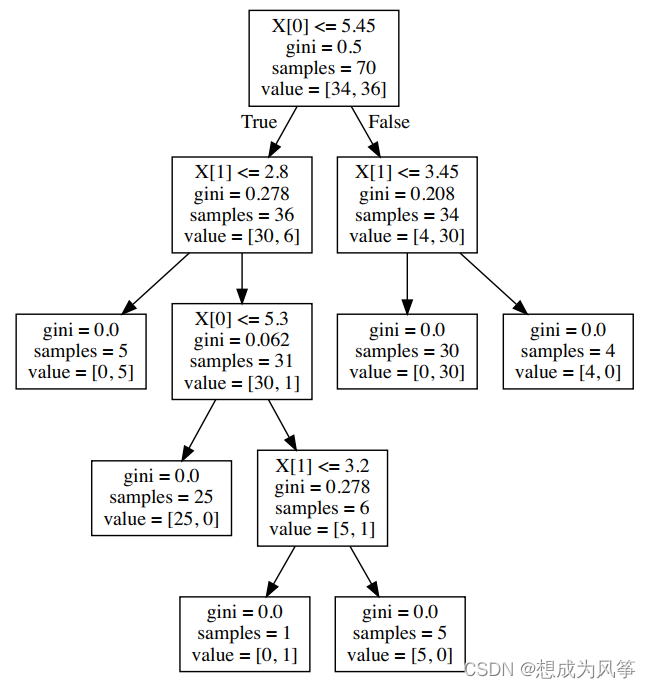
边栏推荐
猜你喜欢
![[yarn] CDP cluster yarn configuration capacity scheduler batch allocation](/img/85/0121478f8fc427d1200c5f060d5255.png)
[yarn] CDP cluster yarn configuration capacity scheduler batch allocation
Machine learning notes week02 convolutional neural network

Come and walk into the JVM
MySQL与c语言连接(vs2019版)
Composition des mots (sous - total)
C语言读取BMP文件

PHP - whether the setting error displays -php xxx When PHP executes, there is no code exception prompt

Nanny level problem setting tutorial
vs2019 桌面程序快速入门

Case analysis of data inconsistency caused by Pt OSC table change
随机推荐
wangeditor富文本组件-复制可用
MySQL realizes read-write separation
Distribute wxWidgets application
[蓝桥杯2017初赛]方格分割
Library function -- (continuous update)
Connexion sans mot de passe du noeud distribué
【Flink】CDH/CDP Flink on Yarn 日志配置
mysql实现读写分离
Internet protocol details
小L的试卷
Stage 4 MySQL database
FTP file upload file implementation, regularly scan folders to upload files in the specified format to the server, C language to realize FTP file upload details and code case implementation
L2-004 这是二叉搜索树吗? (25 分)
Hutool中那些常用的工具类和方法
{一周总结}带你走进js知识的海洋
JS array + array method reconstruction
Word排版(小計)
Learn winpwn (3) -- sEH from scratch
Machine learning notes week02 convolutional neural network
Solution to the practice set of ladder race LV1 (all)