当前位置:网站首页>《统计学》第八版贾俊平第十一章一元线性回归知识点总结及课后习题答案
《统计学》第八版贾俊平第十一章一元线性回归知识点总结及课后习题答案
2022-07-06 09:23:00 【无二三事】
目录
一、知识框架
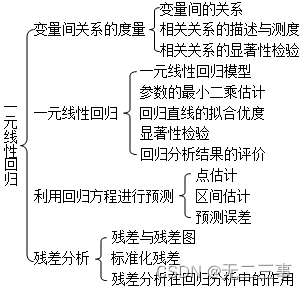
二、课后习题
1从某一行业中随机抽取12家企业,所得产量与生产费用的数据如表所示。
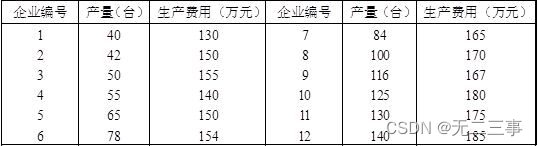
要求:
(1)绘制产量与生产费用的散点图,判断二者之间的关系形态。
(2)计算产量与生产费用之间的线性相关系数。
(3)对相关系数的显著性进行检验(α=0.05),并说明二者之间的关系强度。
解:(1)绘制散点图,如图所示。
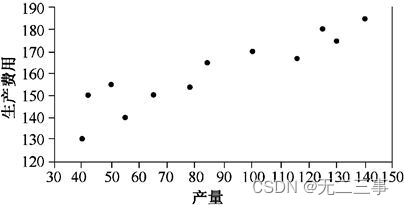
从散点图可以看出,产量与生产费用之间为正的线性相关关系。
(2)令产量为变量X,生产费用为变量Y。由表中数据可计算得到:
x=85.42y=160.08
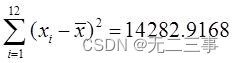
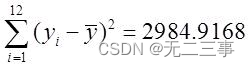
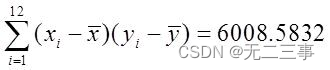
故相关系数为:
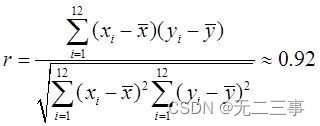
(3)首先提出如下假设:H0:ρ=0;H1:ρ≠0。计算检验的统计量的值:
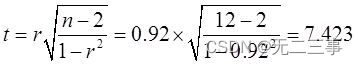
当α=0.05时,t0.05/2(12-2)=2.228。由于检验统计量的值t=7.423>tα/2=2.228,所以拒绝原假设。表明产量与生产费用之间的线性关系显著。
2随机抽取10家航空公司,对其最近一年的航班正点率和顾客投诉次数进行了调查,所得数据如表所示。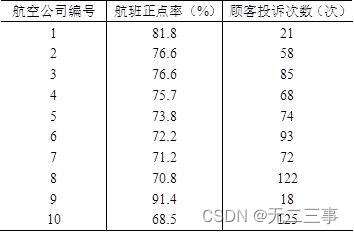
要求:
(1)绘制散点图,说明二者之间的关系形态。
(2)用航班正点率作自变量,顾客投诉次数作因变量,求出估计的回归方程,并解释回归系数的意义。
(3)检验回归系数的显著性(α=0.05)。
(4)如果航班正点率为80%,估计顾客的投诉次数。
(5)求航班正点率为80%时,顾客投诉次数95%的置信区间和预测区间。
解:(1)绘制散点图,如图所示。
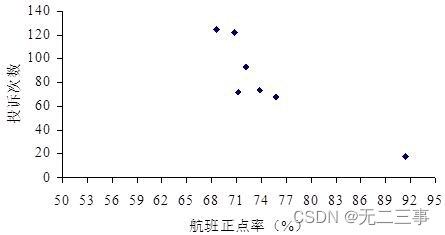
从散点图可以看出,航班正点率与被投诉次数之间为负的线性相关关系。
(2)由Excel输出的回归结果如表1所示。
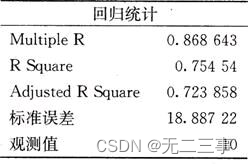


由线性回归方程为:y=430.1892-4.7x
回归系数β1=-4.7表示航班正点率每增加1%,顾客投诉次数平均下降4.7次。
(3)回归系数检验的P-值=0.001108<α=0.05,拒绝原假设,回归系数显著。
(4)y80=430.1892-4.7×80=54.1892(次)。
(5)当α=0.05时,t0.05/2(10-2)=2.306,se=18.88722。
置信区间为:
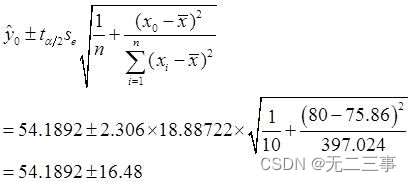
即(37.7,70.7)。
预测区间为:
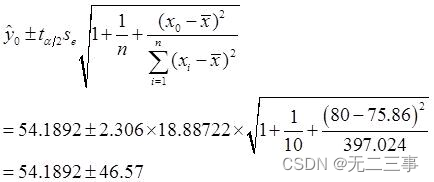
即(7.6,100.8)。
3下面是20个城市写字楼出租率和每平方米月租金的数据,如表所示。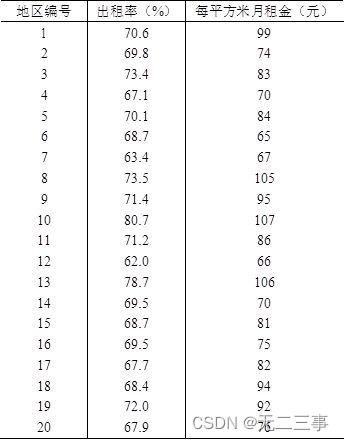
设月租金为自变量,出租率为因变量,用Excel进行回归,并对结果进行解释和分析。
解:Excel输出的回归结果,如表所示。


由表可以得到,线性回归方程为:Y=49.3177+0.2492X
回归系数β1=0.2492表示:月租金每增加1元,出租率平均增加0.2492%。
R2=63.22%,表明在出租率的变差中被出租率与租金之间的线性关系所解释的比例为63.22%,回归方程的拟合程度一般。
估计标准误差se=2.6858表示,当用月租金来预测出租率时,平均的预测误差为2.6858%,表明预测误差并不大。
由方差分析表可知,Significance F=2.79889E-05<α=0.05,即回归方程的线性关系显著。回归系数检验的P-值=0.0000<α=0.05,表明回归系数显著,即月租金是影响出租率的显著性因素。4某汽车生产商欲了解广告费用(x)对销售量(y)的影响,收集了过去12年的有关数据。通过计算得到的有关结果,如表所示。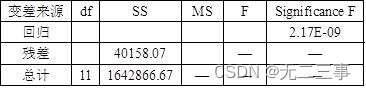

要求:
(1)完成上面的方差分析表。
(2)汽车销售量的变差中有多少是由于广告费用的变动引起的?
(3)销售量与广告费用之间的相关系数是多少?
(4)写出估计的回归方程并解释回归系数的实际意义。
(5)检验线性关系的显著性(α=0.05)。
解:(1)填写方差分析表,

(2)根据方差分析表计算判定系数为:
R2=SSR/SST=1602708.6/1642866.67=97.56%
这表明汽车销售量的变差中有97.56%是由于广告费用的变动引起的。
(3)相关系数可由判定系数的平方根求得:
![]()
(4)回归方程为:y=363.6891+1.420211x
回归系数β1=1.420211表示广告费用每增加1个单位,销售量平均增加1.420211个单位。
(5)由于Significance F=2.17E-09<α=0.05,表明广告费用与销售量之间的线性关系显著。
5根据表的数据建立回归方程,计算残差、判定系数R2,估计标准误差se,并分析回归方程的拟合程度。![]()
解:Excel输出的回归结果如表所示。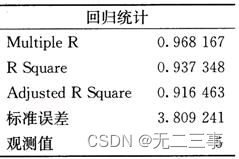


由表可以得到,线性回归方程为:y=13.6254+2.3029x
回归系数表明,x每增加1个单位,y平均增加2.3029个单位;判定系数R2=93.74%,表明回归方程的拟合程度较高;估计标准误差se=3.8092,表明用x来预测y时平均的预测误差为3.8092。
6随机抽取7家超市,得到其广告费支出和销售额数据如表所示。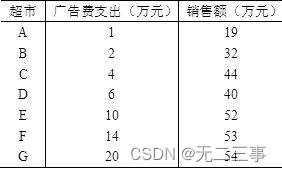
要求:
(1)用广告费支出作自变量x,销售额作因变量y,求出估计的回归方程。
(2)检验广告费支出与销售额之间的线性关系是否显著(α=0.05)。
(3)绘制关于x的残差图,你觉得关于误差项ε的假定被满足了吗?
(4)你是选用这个模型,还是另寻找一个更好的模型?
解:(1)Excel输出的回归结果如表所示。
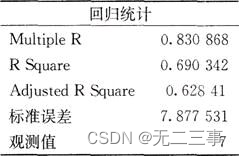


由表可以得出,估计的回归方程为:y=29.3991+1.547478x
(2)由于Significance F=0.020582<α=0.05,所以广告费支出与销售额之间的线性关系显著。
(3)绘制关于x的残差图,如图所示。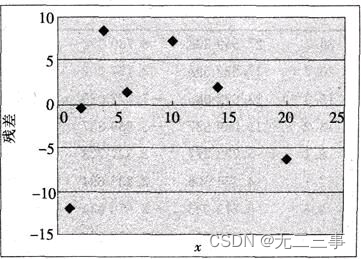
从残差图可以看出,关于误差项ε的假定并不成立。
(4)虽然线性关系通过了显著性检验,但从残差图来看,关于x与y之间存在线性关系的假设仍值得怀疑。因此可考虑选用非线性模型。
边栏推荐
- Record an edu, SQL injection practice
- 【educoder数据库实验 索引】
- Spot gold prices rose amid volatility, and the rise in U.S. prices is likely to become the key to the future
- Intranet information collection of Intranet penetration (4)
- Strengthen basic learning records
- 记一次edu,SQL注入实战
- HackMyvm靶机系列(6)-videoclub
- Nuxtjs quick start (nuxt2)
- 小程序web抓包-fiddler
- Tencent map circle
猜你喜欢
Harmonyos JS demo application development

JDBC transactions, batch processing, and connection pooling (super detailed)
Attack and defense world misc practice area (GIF lift table ext3)
Record an edu, SQL injection practice
List and data frame of R language experiment III
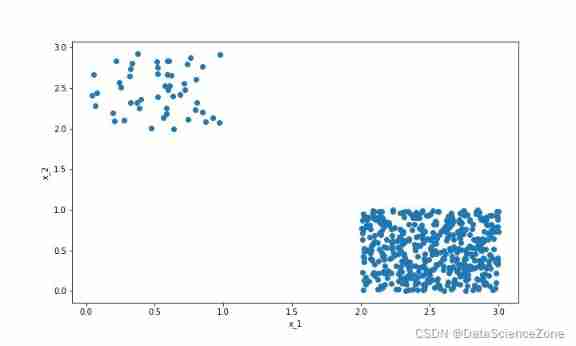
Data mining - a discussion on sample imbalance in classification problems
循环队列(C语言)
Intranet information collection of Intranet penetration (4)
xray與burp聯動 挖掘
Build domain environment (win)
随机推荐
1143_ SiCp learning notes_ Tree recursion
HackMyvm靶机系列(5)-warez
Matlab opens M file garbled solution
Experiment five categories and objects
【MySQL数据库的学习】
Strengthen basic learning records
WEB漏洞-文件操作之文件包含漏洞
Low income from doing we media? 90% of people make mistakes in these three points
Intranet information collection of Intranet penetration (4)
Analysis of penetration test learning and actual combat stage
MSF generate payload Encyclopedia
XSS (cross site scripting attack) for security interview
C language file operation
图书管理系统
. How to upload XMIND files to Jinshan document sharing online editing?
Package bedding of components
循环队列(C语言)
xray與burp聯動 挖掘
How to understand the difference between technical thinking and business thinking in Bi?
What language should I learn from zero foundation. Suggestions