当前位置:网站首页>函数:用牛顿迭代法求方程的根
函数:用牛顿迭代法求方程的根
2022-07-06 09:24:00 【|光|】
要求
用牛顿迭代法求方程的根。方程为ax3+bx2+cx+d=0,系数由用户输入,求x在1附近的根。
,
代码
#include<math.h>
#define EPSILON 1E-6
/* * 函数f(x)=a*x**3+b*x**2+c*x+d */
double f(double a,double b,double c, double d, double x)
{
double t;
t=a*x*x*x+b*x*x+c*x+d;
return t;
}
/* * 函数f(x)=a*x**3+b*x**2+c*x+d的导函数 */
double derivatives(double a,double b,double c, double d, double x)
{
double t;
t=3*a*x*x+2*b*x+c;
return t;
}
/* * 在该函数中用迭代法求解方程在1附近的根,可以调用上面的f函数和f的导函数 */
double fun(double a,double b,double c,double d)
{
double x1,x=1;
do
{
x1=x;
x = x1 - f(a,b,c,d,x)/derivatives(a,b,c,d,x);
}
while(fabs(x1-x)>=1e-3);
return x;
}
测试
测试输入
10 5 -11 -3.28351
输出
方程在1附近的根为0.97
边栏推荐
- Chain team implementation (C language)
- How does SQLite count the data that meets another condition under the data that has been classified once
- Sentinel overall workflow
- Lintcode logo queries the two nearest saplings
- Intranet information collection of Intranet penetration (2)
- Feature extraction and detection 14 plane object recognition
- 四元数---基本概念(转载)
- [paper reproduction] cyclegan (based on pytorch framework) {unfinished}
- 《统计学》第八版贾俊平第一章课后习题及答案总结
- Statistics 8th Edition Jia Junping Chapter 12 summary of knowledge points of multiple linear regression and answers to exercises after class
猜你喜欢

Network technology related topics
内网渗透之内网信息收集(四)
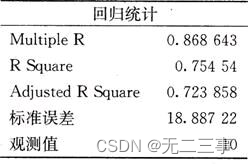
Statistics, 8th Edition, Jia Junping, Chapter 11 summary of knowledge points of univariate linear regression and answers to exercises after class

Wu Enda's latest interview! Data centric reasons
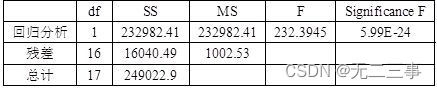
《统计学》第八版贾俊平第十三章时间序列分析和预测知识点总结及课后习题答案
Attack and defense world misc practice area (simplerar, base64stego, no matter how high your Kung Fu is, you are afraid of kitchen knives)
Hackmyvm target series (3) -visions
内网渗透之内网信息收集(二)
浅谈漏洞发现思路
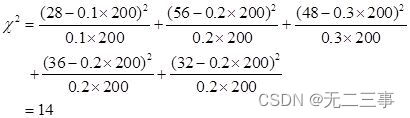
Statistics 8th Edition Jia Junping Chapter IX summary of knowledge points of classified data analysis and answers to exercises after class
随机推荐
Record an edu, SQL injection practice
msf生成payload大全
Hackmyvm target series (3) -visions
《统计学》第八版贾俊平第十三章时间序列分析和预测知识点总结及课后习题答案
Statistics, 8th Edition, Jia Junping, Chapter 6 Summary of knowledge points of statistics and sampling distribution and answers to exercises after class
JDBC看这篇就够了
xray与burp联动 挖掘
Interpretation of iterator related "itertools" module usage
XSS之冷门事件
A complete collection of papers on text recognition
关于超星脚本出现乱码问题
《统计学》第八版贾俊平第六章统计量及抽样分布知识点总结及课后习题答案
数据库多表链接的查询方式
Sword finger offer 23 - print binary tree from top to bottom
How to understand the difference between technical thinking and business thinking in Bi?
Intel oneapi - opening a new era of heterogeneity
What language should I learn from zero foundation. Suggestions
Hackmyvm target series (7) -tron
Sqqyw (indifferent dot icon system) vulnerability recurrence and 74cms vulnerability recurrence
XSS (cross site scripting attack) for security interview