当前位置:网站首页>Understanding of expectation, variance, covariance and correlation coefficient
Understanding of expectation, variance, covariance and correlation coefficient
2022-07-08 01:23:00 【You roll, I don't roll】
Catalog
1、 Mathematical expectation ( mean value )
4、 The correlation coefficient ρ
One sentence summary : expect Reflects the average level , variance It reflects the fluctuation degree of data , covariance It reflects the correlation between two random variables ( Dimensionality ), The correlation coefficient It reflects the dimensionless correlation between two random variables .
1、 Mathematical expectation ( mean value )
For random variables and their probabilities weighted mean :
![]()
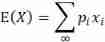
The expectation here is the mean , In statistics, samples are used to replace the whole in most cases , Therefore, the average value of the sample is calculated as :
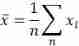
2、 variance D(X) or Var(X)
It is used to understand the deviation between the actual index and the average value , That is, it reflects the dispersion of data values .
![]()
if X Value set , Then its variance is small , conversely , X The more dispersed, the greater the variance .
D(X) Satisfy the following properties :
![]()
When X And Y Satisfy Independent homologous distribution (iid) when ,![]() , here :
, here :
![]()
there ![]() That's what we'll talk about later covariance .
That's what we'll talk about later covariance .
in addition Standard deviation ( Mean square error ) The calculation formula of is :![]() , And X Have the same dimension .
, And X Have the same dimension .
In sample analysis , The calculation formula of variance is :
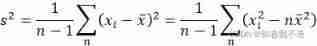
Be careful : This is divided by 1/(n-1).
Why does divide appear in variance calculation n And divided by n-1 Two cases ?:
Divide n It calculates the population variance
, Divide n-1 It calculates the sample variance
( That is, the unbiased estimation of the total variance ). But in reality, it is often unrealistic to calculate the total variance , One of the research contents of statistics is to infer the population with samples , Therefore, we often use sample variance to replace the overall situation .
Why is the sample variance calculated by n-1 Well ? Because we must calculate the sample mean before calculating the sample variance
( let me put it another way , Will sum the samples ), This leads to the n If the item is determined n-1 Item's words , The first n Items can be determined , That is, the degree of freedom is n-1, So the probability of each occurrence is 1/(n-1) , So you have to divide by n-1. In terms of linear algebra , this n Quantity is not independent , If the n If a quantity is regarded as a vector, it is linearly related , Can be n-1 A linearly independent vector representation .
If divided by n It means that we know the mean value of the population sample in advance μ( This μ It is known. , Not calculated , Because in reality, it is often unrealistic to calculate the overall average ), At this time, the probability of occurrence of all quantities is 1/n, So the variance at this time
The calculation of is divided by n. But this situation can only be regarded as the ideal calculation method , In reality, it is basically impossible , In reality, most cases estimate the population based on samples , Therefore, our common variance calculation formula is to divide by n-1 了 .
3、 covariance Cov(X,Y)
Covariance is used to describe the correlation between two variables . Covariance is a dimensional quantity .
![]()
if X And Y Are independent of each other , be ![]() .
.
4、 The correlation coefficient ρ
The correlation coefficient is also used to describe the correlation between two variables , But unlike covariance , The correlation coefficient is a dimensionless quantity , The formula is as follows .
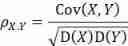
in addition , call
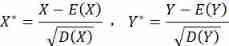
by X、Y Standardization of . Then there are :
![]()
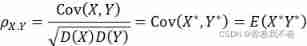
The nature of the correlation coefficient :
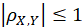 .
.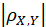 The greater the value of, the greater the degree of linear correlation ,
The greater the value of, the greater the degree of linear correlation ,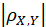 When the value is large, it is called X And Y The linear correlation is good ;
When the value is large, it is called X And Y The linear correlation is good ;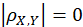 Time description X And Y There is no linear relationship , But there may be other relationships , For example, for obedience
Time description X And Y There is no linear relationship , But there may be other relationships , For example, for obedience  The random variable on X Come on , if X1=sinX,X2=cosX, although
The random variable on X Come on , if X1=sinX,X2=cosX, although 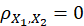 , But satisfied
, But satisfied 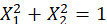 .
.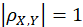 The necessary and sufficient conditions for : There is a constant a、b, bring
The necessary and sufficient conditions for : There is a constant a、b, bring 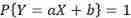
5、 Covariance matrix
Covariance matrix is used to describe the covariance between different dimensions of multidimensional random variables .
set up n Dimensional random variable ![]() The second-order covariance of is
The second-order covariance of is
![]()
Then the matrix
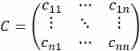
be called n Dimensional random variable ![]() The covariance matrix of . because
The covariance matrix of . because ![]() , Therefore, the covariance matrix is also a symmetric matrix , The variance forms the elements on its diagonal , Covariance constitutes the non diagonal element . In a general way ,n The distribution of dimensional random variables is unknown , Or it's too complicated , So difficult to deal with mathematically , Therefore, covariance matrix is very important in practical application . Covariance matrix is widely used in statistics, machine learning and other fields .
, Therefore, the covariance matrix is also a symmetric matrix , The variance forms the elements on its diagonal , Covariance constitutes the non diagonal element . In a general way ,n The distribution of dimensional random variables is unknown , Or it's too complicated , So difficult to deal with mathematically , Therefore, covariance matrix is very important in practical application . Covariance matrix is widely used in statistics, machine learning and other fields .
边栏推荐
- 14. Draw network model structure
- High quality USB sound card / audio chip sss1700 | sss1700 design 96 kHz 24 bit sampling rate USB headset microphone scheme | sss1700 Chinese design scheme explanation
- 4. Apprentissage stratégique
- General configuration toolbox
- 国内首次,3位清华姚班本科生斩获STOC最佳学生论文奖
- Codeforces Round #804 (Div. 2)
- Talk about smart Park
- Design method and application of ag9311maq and ag9311mcq in USB type-C docking station or converter
- Several frequently used OCR document scanning tools | no watermark | avoid IQ tax
- Chapter VIII integrated learning
猜你喜欢
Common configurations in rectangular coordinate system

5、離散控制與連續控制
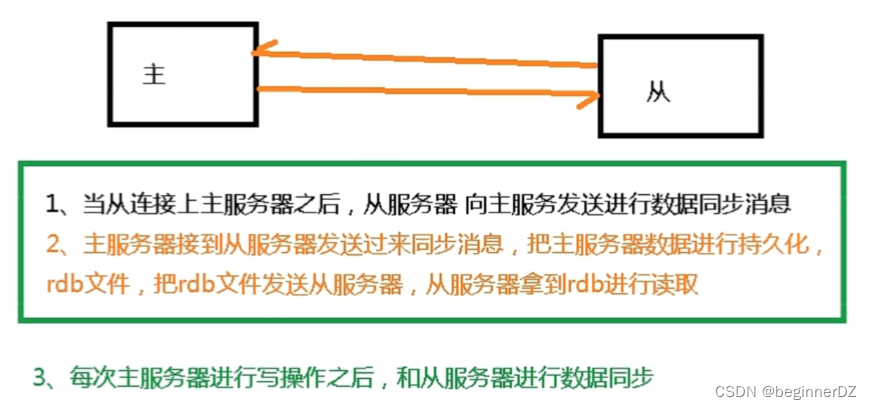
Redis master-slave replication
A speed Limited large file transmission tool for every major network disk
1. Linear regression
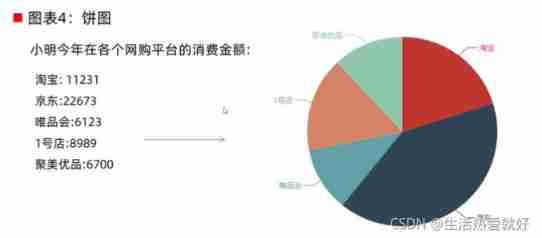
Basic implementation of pie chart

2021 welder (primary) examination skills and welder (primary) operation examination question bank
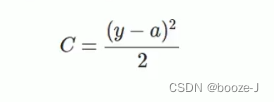
4. Cross entropy
Chapter XI feature selection
Vs code configuration latex environment nanny level configuration tutorial (dual system)
随机推荐
11. Recurrent neural network RNN
2022 examination for safety production management personnel of hazardous chemical production units and new version of examination questions for safety production management personnel of hazardous chem
USB type-C docking design | design USB type-C docking scheme | USB type-C docking circuit reference
网络模型的保存与读取
Su embedded training - Day6
Connect to the previous chapter of the circuit to improve the material draft
Guojingxin center "APEC investment +": some things about the Internet sector today | observation on stabilizing strategic industrial funds
Macro definition and multiple parameters
Four digit nixie tube display multi digit timing
Chapter 5 neural network
Markdown learning (entry level)
For the first time in China, three Tsinghua Yaoban undergraduates won the stoc best student thesis award
Use "recombined netlist" to automatically activate eco "APR netlist"
How to write mark down on vscode
Vscode is added to the right-click function menu
4. Apprentissage stratégique
2021-03-06 - play with the application of reflection in the framework
5. Discrete control and continuous control
130. 被围绕的区域
3. MNIST dataset classification