Fundamentals of digital circuits (II) logic algebra

Fundamentals of digital circuits （ Two ） Logic Algebra

One 、 Logical variables and logical functions

Students who are familiar with computer programming language should know , There is a boolean variable in many programming , It has and only has two values true and false （True and False, Sometimes you use 1 and 0）. Boolean variable itself can actually be regarded as a logical variable , Conform to the characteristics of logical variables . Given a definite input , Usually the output can be uniquely determined .
We assume that there are two inputs $A$ and $B$, There's an output $F$, Between them Logical expression Satisfy $F=f(A,B)$, among $A,B,F$ go by the name of Logical variable , Variable $A$ and $B$ be called Logical arguments ,$F$ go by the name of Logical dependent variable （ Also known as Logical functions ）. Logical variables usually only take 0 or 1 Two values , It can be expressed in the circuit , High and low levels , The disconnection and connection of the switch .

In logic circuits , The definition of high and low level is not only determined by the unique value , They all have a certain constant pressure range . for example ： stay TTL In circuit , The high level is usually 2-5V, The low level is usually 0-0.8V

Two 、 Basic logic operations and basic logic gates

There are three basic logical operations in logic circuits ： Logic and , Logic or , Logic is not . The circuits used to realize these three logical operations are and gates , Or gate , Not gate . Here are the three logic operations and gate circuits .

1. Logic and

Logic and refers to when all the conditions that determine an event are true , This event will happen . The circuit shown in the figure below shows how the circuit controlled by a switch realizes and operates ：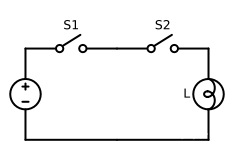

Only when S1 and S2 When both switches are closed at the same time , Light bulb: L It will light up ; If any one of the switches is off , Then the bulb L It won't light up .
take $A$,$B$,$F$ All States of are listed in a table , This table is called Truth table , As shown in the following table ：

From the truth table, we can see that it is similar to multiplication in operation and arithmetic , So logic and is also called Logical multiplication
$$F=A\cdot B=AB$$
Logic and have the following operations ：
$$0\cdot 0=0,0\cdot 1=0,1\cdot 0=0,1\cdot 1=1$$
The symbol of logical and is shown in the figure below

2. Logic or

Logical and refers to all the conditions that determine an event , As long as any one of the conditions is satisfied , Events will happen . The circuit shown in the figure below shows how the circuit controlled by a switch realizes or operates ：

When S1 and S2 When any one of the switches is closed , The lamp L Will light up ; If both switches are disconnected , Then the lamp L It won't light up .
The truth table of or door is shown in the figure below ：

From the truth table, we can see that the or operation is similar to the addition in arithmetic , So logical or is also called Logical addition
$$F=A+B$$
Logic and have the following operations ：
$$0+0=0,0+1=1,1+0=1,1+1=1$$
The symbol of logical and is shown in the figure below ：

3. Logic is not

Logical non means when the condition is satisfied , It doesn't happen ; If the conditions are not met , events . The circuit shown below shows how to realize non operation with switch control circuit ：

When the switch S When disconnected , Power Supply 、 resistance R And light bulb L Formation pathway , The bulb is on ; When the switch S When closed , Light bulb: L Switched S A short circuit , The light bulb doesn't work .
The truth table of non gate is shown in the figure below ：

The expression is ：
$$F=\overline{A}$$
The non operation rule is ：
$$\overline{0}=1,\overline{1}=0$$

4. Compound logic operation

（1） And non operation

The logical expression is ：$F=\overline{AB}$, It is done by logical variables first and , And then do the non operation , The logical symbols are shown in the figure below ：

(2) Or not

The logical expression is ：$F=\overline{A+B}$, It is done by logical variables first or operation , And then do the non operation , The logical symbols are shown in the figure below ：

(3) And or not operation

The logical expression is ：$F=\overline{AB+CD}$, It is done by logical variables first and , Do or calculate again , Finally, do non operation to get , The logical symbols are shown in the figure below ：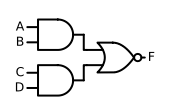

(4) Exclusive or operation

The logical expression is ：$F=A\overline{B}+\overline{A}B=A\oplus B$. The rule of exclusive or operation is ： When the two input logical variables are the same , The output of 0; When the two input logical variables are different , The output of 1. The logical symbols are shown in the figure below ：

(5) The same or operation

The logical expression is ：$F=AB+\overline{AB}=A\odot B$. The same or operation rule is ： When the two input logical variables are the same , The output of 1; When the two input logical variables are different , The output of 0. The logical symbols are shown in the figure below ：

3、 ... and 、 Basic formulas and common formulas of logical algebra

1. The basic formula

（1）0-1 Law   $A\cdot 0=0$      $A+1=1$
（2） The law of self equivalence   $A\cdot 1=A$     $A+0=A$
（3） Overlapping law   $A\cdot A=A$    $A+A=A$
（4） Law of complementarity   $A\cdot \overline{A}=0$    $A+\overline{A}=1$
（5） Commutative law   $A\cdot B=B\cdot A$  $A+B=B+A$
（6） Associative law   $A\cdot (B\cdot C)=(A\cdot B)\cdot C$
       $A+(B+C)=(A+B)+C$
（7） Distribution rate   $A\cdot (B+C)=AB+AC$
       $A+(B+C)=(A+B)(A+C)$
（8） absorptivity   $A\cdot (A+B)=A$    $A+AB=A$
（9） Inversion law   $\overline{AB}=\overline{A}+\overline{B}$    $\overline{A+B}=\overline{A}\cdot \overline{B}$
（10） Double negative rate   $\overline{\overline{A}}=A$

Inversion law is one of the most widely used , It plays an important role in simplifying logical expressions

2. The basic rule

（1） Substitution rule

In any logical equation , If all the variables on both sides of the equation are replaced by a logical function , Then this equation still holds .
for example ：$\overline{A\cdot B}=\overline{A}+\overline{B}$ Medium $A$ Use $F=AC$ replace , Then the original formula becomes ：$\overline{AC\cdot B}=\overline{AC}+\overline{B}=\overline{A}+\overline{B}+\overline{C}$. Still established .

（2） Inversion rules

When we need to solve a logical function $F$ The inverse function of $\overline{F}$ when , Inversion rules can be used .
Only need to $F$ Medium
$$\cdot changeby+,+changeby\cdot ,1changeby0,0changeby1,changeThe\; amounttakeback$$
that will do .

It should be noted that ： When changing the inverse variable , If there are more than two variables, the common negative sign remains unchanged

for example ： seek $F=A+\overline{B+\overline{C}+\overline{D+\overline{E}}}+(G\cdot H)$ The inverse function of
    $\overline{F}=\overline{A}\cdot \overline{\overline{B}\cdot C\cdot \overline{\overline{D}\cdot E}}\cdot (\overline{G}+\overline{H})$

（3） The duality rule

When we need to solve a logical function $F$ Dual form of $F^{\prime }$ when ,
Only need to $F$ Medium
$$\cdot changeby+,+changeby\cdot ,1changeby0,0changeby1$$
that will do .
Two logical functions are equal $\iff$ The duality of two logical functions is equal （ Sufficient and necessary conditions ）

for example ： seek $F=A\cdot B+\overline{A}\cdot C+B\cdot C$ Dual form of
    $F^{\prime }=(A+B)\cdot (\overline{A}+C)\cdot (B+C)$

3. Common formula

The formula 1 $AB+A\overline{B}=A$
prove ：  $AB+A\overline{B}=A(B+\overline{B})=A$
The formula 2 $A+A\overline{B}=A+B$
prove ：  $A+\overline{A}B=(A+\overline{A})\cdot (A+B)=A+B$
The formula 3 $AB+\overline{A}C+BC=AB+\overline{A}C$
prove ：  $AB+\overline{A}C+BC=AB+\overline{A}C+BC(A+\overline{A})=AB+\overline{A}C+ABC+\overline{A}BC=AB+\overline{A}C$
The formula 4 $\overline{AB+\overline{A}C}=A\overline{B}+\overline{A}\overline{C}$
prove ： A little
The formula 5 $\overline{A\oplus B}=A\odot B$
prove ： A little

Four 、 Briefly introduce several ideas of using formula method to simplify

The names of the methods here are all given by the author himself , Perhaps it is more in line with the meaning of the formula

（1） Go heteromorphic

$A+AB$ type , here $A,B$ It can be a logical expression rather than a separate logical variable . In direct discharge “ Alien species ”:$B$, The rest as a result is $A+AB=A$

（2） Go non type

$A+\overline{A}B$ type , here $A,B$ It can be a logical expression rather than a separate logical variable . In direct discharge “ Non item ”:$\overline{A}$, The rest as a result is $A+\overline{A}B=A+B$

（3） De inversion

$AB+\overline{A}B$ type , here $A,B$ It can be a logical expression rather than a separate logical variable . In direct discharge “ The opposite ”:$\overline{A}$ and $A$, The rest as a result is $AB+\overline{A}B=B$

（4） Three deficiencies and one type

It is generally used to have three variables , But in the and or formula with only two logical variables for each term in the logical expression , You can operate after the lack of a logical variable $(X+\overline{X})$,$X$ Indicates the missing logical variable .
A simple example ：$F=A\overline{B}+B\overline{C}$ Only need $A\overline{B}$ After and operation a $(C+\overline{C})$,$B\overline{C}$ After and operation a $(A+\overline{A})$ that will do .

5、 ... and 、 Use Karnaugh map to simplify logical expressions

1. Minimum term

Want to use Karnaugh map for simplification , First of all, we need to understand the concept of minimum term .
In the Carnot , Each square represents a minimum term . There is $n$ In the logical function of logical variables , The product term of all variables is called the minimum term . Why is it called the minimum term , Because every variable only appears once , And they all appear in the form of itself or anti variable . Analogous to making permutations , List all possible variables that can occur only once , Is all its smallest terms .

for example ： Two variables $A,B$ The minimum term of is $2^2=4$ individual （$AB,A\overline{B},\overline{A}B,\overline{AB}$）

For convenience , Use $m_i$ Record the smallest item in the form of . Its notation is ： When a logical variable appears as an original variable in the minimum term , Write it down as 1; When it appears as an inverse variable , Write it down as 0. Then convert it into decimal numbers , What is this decimal number , that $m_i$ The subscript $i$ Just for how much .

for example ：$\overline{A}BC$ Recorded as binary number 011, and 011 The corresponding decimal number is 3, so $\overline{A}BC$ Write it down as $m_3$

When we are familiar with the concept of minimum term , We can convert any logic function into the form of the minimum term , And use $m_i$ Formal representation of .
for example ：$ABC+AB\overline{C}+\overline{A}BC+\overline{AB}C=m_7+m_6+m_3+m_1$

2. Karnaugh map

（1） Two variable Karnaugh map

The following figure is a two variable Karnaugh map ：

The picture shows ,$A$ and $B$ There are two values 0 and 1, They can form four combinations , Each combination is a minimum term . If the minimum term is used to represent the Karnaugh map, it is shown in the following figure ：

You can see that its binary value corresponds to the minimum term $m_i$ Medium $i$

（2） Three variable Karnaugh map

Here is a three variable Karnaugh map ：

The picture shows ,$A$,$B$ and $C$ There are two values 0 and 1, They can form eight combinations , Each combination is a minimum term . If the minimum term is used to represent the Karnaugh map, it is shown in the following figure ：

You can also see that its binary value corresponds to the minimum term $m_i$ Medium $i$

（4） Four variable Karnaugh map

The minimum term form of four variable Karnaugh map is given ：

Its determination method is consistent with the determination method of the minimum term of two variables and three variables .

Three variable and four variable Karnaugh map 00,01,11,10 The arrangement of ensures that there is only one different number between two , The adjacent conditions are met

3. Karnaugh map represents logic function

When we know the logic function , You can first simplify the logical function into a minimum term expression , Then fill the value in the Karnaugh map corresponding to the minimum term as 1, Fill in the rest as 0 that will do , You can also fill in the Karnaugh map directly according to the expression ; If what we know directly is minimal term expression , You can directly fill in the corresponding position in the Karnaugh map 1, Fill in the rest 0.
for example ：
$F=ABC+AB\overline{C}+\overline{A}BC+\overline{AB}C=m_7+m_6+m_3+m_1$
We know its minimal term expression , You can directly fill in numbers in the blank Karnaugh map , As shown in the figure below ：

4. Reduction method

（1） Merge minimums

We can put the adjacent 8 individual 、4 individual 、2 individual 、1 The smallest collar of , A merger . As shown in the figure below ：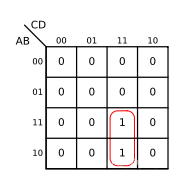

The red circle in the figure indicates that these two items are merged , It is easy to see that they are adjacent . I have to pay attention to , The boundary of Karnaugh map is not the boundary in the practical sense .
for example ：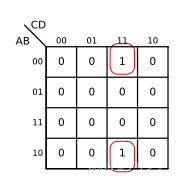

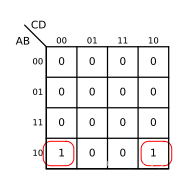
These two and other similar situations belong to the adjacent situation when two variables are merged

For the case of four variables , The following two series are obviously adjacent ：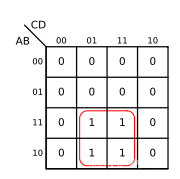

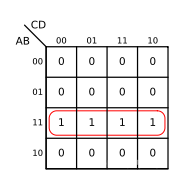
besides , The following cases also belong to four adjacent variables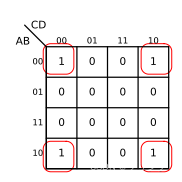

There are several combinations of eight variables （ Including similar situations ）：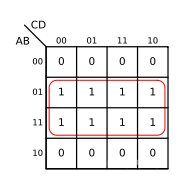

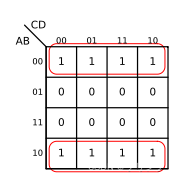
give an example ： Simplify with Karnaugh map $F=\overline{ABCD}+A\overline{BC}D+\overline{A}B\overline{C}+AB\overline{D}+\overline{A}BC+BCD$

Draw the logical expression in the Karnaugh diagram , And merge in the way we just explained ：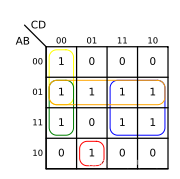

here , We just need to write the circled part of the Karnaugh map in the form of a logical expression , Then take or operate them
$F=A\overline{BC}D+\overline{ACD}+\overline{A}B+BC+B\overline{D}$

（2） Simplification of Karnaugh map with irrelevant terms

In some logic functions , The minimum item corresponding to some combinations of variable values will not appear or is not allowed , These minimum terms are called constraint terms . It is generally used in Karnaugh map "$\times$" Express . When simplifying in this case , You can merge the smallest items with the help of irrelevant items .
give an example ：
$F(A,B,C,D)=\sum (m_{15},m_{13},m_{10},m_6,m_4)+{\sum }_d(m_8,m_7,m_5,m_2,m_1,m_0)$
You can treat irrelevant items as 1 To process and merge .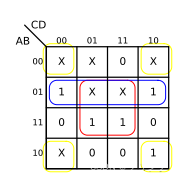

Then write the circled ones as logical expressions .
$F=\overline{A}B+BD+\overline{BD}$

first draft 2022/5/5