当前位置:网站首页>Numpy快速上手指南
Numpy快速上手指南
2022-07-06 09:24:00 【ブリンク】
Numpy快速上手指南
文章目录
Numpy简介
Numpy是Python中一个基本的科学计算库,它提供了多维数组对象,以及各种派生对象。使用C语言预编译的代码,向量化的描述,使得Numpy拥有较快的运算速度,更清晰的广播(broadcasting)机制使得代码简化,也意味着犯错的几率更低。在数据分析、机器学习领域,Numpy成为Python一个热门的选择。
本文通过一些例子,带大家快速上手Numpy。在此之前,需要我们具有一定的Python基础,我们将搭配matplotlib库进行演示。
故我们需要在演示开始之前导入库
import numpy as np #习惯性把numpy简写为np
import matplotlib.pyplot as plt
1.基本属性
Numpy的核心是数组,我们首先学习如何创建数组,使用np.array()进行创建下边是创建一个一维数组:
>>> a = np.array([1,2,3])
>>> a
array([1,2,3])
我们也可以创建一个高维的数组:
>>> a = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> a
array( [[1,2,3],
[4,5,6],
[7,8,9]])
我们可以使用Python的type()方法直接查看数组的类型
>>> type(a)
numpy.ndarray
此时我们想知道创建的数组的维度是多少,那么可以查看ndarray类中的ndim属性
>>> a.ndim
2
返回的是数组的维度,可以把它理解为[]的个数
此时我们想知道创建的数组是什么形状的,即使这个简单的数组我们可以数出它是3*3的,可以查看ndarray中的shape属性
>>> a.shape
(3,3)
此时我们想知道这个数组中有多少个元素,可以查看ndarray的属性size
>>> a.size
9
实际上它等于shape属性的乘积
此时我们想知道数组中存的元素是什么类型的,可以查看ndarray的dtype属性
>>> a.dtype
dtype('int32')
numpy.int32, numpy.int16以及 numpy.float64等是Numpy额外提供的一些类型,当然在创建数组时,也可以使用Python自带的数据类型。
此时我们想知道数组元素中每个元素占用了多少字节,可以查看ndarray的itemsize属性
>>> a.itemsize
4
实际上int32类型的字节占用是32/8=4,而如果是float64型的元素,则为64/8=8字节
2.数组创建方式
有很多种创建数组的方式,上述通过给定Python列表和元组的方式创建数组的方式应当注意,我们给定的数据必须要包含在[]中,而不是一列数
>>> a = np.array(1,2,3) # 这是错误的
>>> a = np.array([1,2,3]) # 这是正确的
我们在创建数组时,可以指定数据的类型,直接在array()中设定dtype参数为想要的类型即可
>>> a = np.array([1,2,3,4], dtype = np.complex)
>>> a
array([1.+0.j, 2.+0.j, 3.+0.j, 4.+0.j])
>>> a.dtype
dtype('complex128')
通常,我们并不知道数组里面数据是什么,但是却知道它的大小(size),我们可以用固定的大小提前初始化这些数组:
zeros()可以创建一个指定大小的数组,数组里面的元素全部都是0
>>> a = np.zeros((2,3))
>>> a
array([[0., 0., 0.],
[0., 0., 0.]])
ones()可以创建一个指定大小的数组,数组里面的元素全部都是1,当然它们在创建时,也可以指定其中元素的数据类型
>>> a = np.ones((3,2), dtype = np.int32)
>>> a
array([[1, 1],
[1, 1],
[1, 1]])
我们也可以使用empty()来创建一个指定大小的空数组,里面的数据是随机产生的,这与内存的状态是有关的
>>> np.empty((2,2,2))
array([[[4.94065646e-324, 2.12199579e-314],
[4.24399158e-314, 2.12199579e-314]],
[[6.36598737e-314, 4.24399158e-314],
[2.12199579e-314, 4.94065646e-324]]])
我们可以创建具有一定规律的数组,使用arange(),它与Python的range()是非常相似的
>>> np.arange(0, 10, 2)
array([0, 2, 4, 6, 8])
>>> np.arange(1,2,0.2)
array([1. , 1.2, 1.4, 1.6, 1.8])
使用arange()有一个缺陷是,我们并不知道数组中存放了多少个元素,使用linspace可以解决这个问题,它可以直接生成你指定的需要多少个元素。
>>> np.linspace(0,3,6) # 生成0-3中间均匀分布的6个数
array([0. , 0.6, 1.2, 1.8, 2.4, 3. ])
3.插入、排序和移除数组元素
在已经建立好的数组中可以继续插入数据,使用insert()方法,其中第一个参数表示在哪个数组中插入,第二个参数表示索引,第三个参数表示插入的值(也可以是数组),axis可以规定是哪个方向的:
>>>a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
>>> np.insert(a,1,999,axis=1) # 在a数组索引1的列处插入999
array([[ 1, 999, 2, 3, 4],
[ 5, 999, 6, 7, 8],
[ 9, 999, 10, 11, 12]])
Numpy中的sort()方法可以直接将元素排序
>>> a = np.array([5,4,1,2,7,9,3,6,0])
>>> a
array([5, 4, 1, 2, 7, 9, 3, 6, 0])
>>> np.sort(a)
array([0, 1, 2, 3, 4, 5, 6, 7, 9])
使用argsort方法可以将排序后的索引输出为数组:
>>> np.argsort(a)
array([8, 2, 3, 6, 1, 0, 7, 4, 5], dtype=int64)
使用delete()方法可以删除数组中的元素,它的使用方法和insert()方法是相似的,只不过无需输入第三个参数——值(value)
>>>np.delete(a,[1],axis=0) # 删除a数组的第二行
array([[ 1, 2, 3, 4],
[ 9, 10, 11, 12]])
4.改变数组形状
我们可以通过ndarray的reshape()方法改变数组的形状
>>> a = np.arange(12)
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>> a.reshape(4,3) # 将数组变为4*3
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
可以改变为更高维
>>> a.reshape(2,2,3)
array([[[ 0, 1, 2],
[ 3, 4, 5]],
[[ 6, 7, 8],
[ 9, 10, 11]]])
5.基本运算
我们可以对数组进行一系列的数学运算,包括加减乘除以及乘方运算等运算
>>> a = np.array([1,2,3,4])
>>> b = np.array([8,7,6,5])
>>> b-a
array([7, 5, 3, 1])
>>> a+b
array([9, 9, 9, 9])
>>> a*b
array([ 8, 14, 18, 20])
>>> a/b
array([0.125 , 0.28571429, 0.5 , 0.8 ])
>>> a**2
array([ 1, 4, 9, 16], dtype=int32)
可以看到,在进行这些运算的时候,会对数组的每一个对应元素进行运算。Numpy可以使用 @ @ @或者 d o t dot dot对两个矩阵进行乘法操作,得到的结果是矩阵相乘的结果。
>>> a = np.array([[1,2],[3,4]])
>>> b = np.array([[3,2],[1,2]])
>>> [email protected] # 矩阵乘法
array([[ 5, 6],
[13, 14]])
>>> a.dot(b)
array([[ 5, 6],
[13, 14]])
值得注意的是,当我们操作两种不同类型的数组时,结果数组会向上投射(upcasting),也就是说,会把精确度比较低的数据类型转化为精确度比较高的类型。下面举个例子:
>>> a = np.array([[1,2],[3,4]],dtype=np.int32)
>>> b = np.array([[3,2],[1,2]],dtype=np.float64)
>>> c = a + b
>>> c.dtype
dtype('float64')
我们可以使用min()找出数组中最小的那个数,使用max()找出数组中最大的那个数,使用sum()对数组中所有的元素进行求和,使用mean()对数组中的元素取平均数。
>>> a = np.random.random((2,3)) # 产生2*3的随机数
>>> a
array([[0.09291709, 0.36686894, 0.88096043],
[0.20985186, 0.1433596 , 0.67468045]])
>>> a.min()
0.09291709064299836
>>> a.max()
0.8809604347992017
>>> a.sum()
2.3686383681150147
>>> a.mean()
0.39477306135250245
有的时候我们想知道特定的行或者列的一些数字特征,我们就需要在这些方法中加入参数axis,当axis=0时意味着将对数组的列进行操作;而当axis=1时,将对数组的行进行操作,下面举个例子:
>>> a = np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> a.sum(axis = 0) # 对列进行操作
array([12, 15, 18, 21])
>>> a.max(axis = 1)
array([ 3, 7, 11]) # 对行进行操作
还有一种特殊的运算:累加。它是把从第一个元素开始和每一个元素相加之后的结果输出,它也同样可以使用axis控制行操作还是列操作
>>> a = np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> a.cumsum()
array([ 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66], dtype=int32)
6.常见公式
在数学中,我们往往会计算一些例如 c o s cos cos, s i n sin sin, t a n tan tan, e n e^n en, x \sqrt{x} x之类的运算,Numpy也可以实现这些数学函数的计算
>>> a = np.arange(4)
>>> a
array([0, 1, 2, 3])
>>> np.sin(a)
array([0. , 0.84147098, 0.90929743, 0.14112001]) # 正弦函数
>> np.exp(a)
array([ 1. , 2.71828183, 7.3890561 , 20.08553692]) # e指数函数
>> np.sqrt(a)
array([0. , 1. , 1.41421356, 1.73205081]) # 根号操作
>> np.add(a,a)
array([0, 2, 4, 6]) # 相加操作
还有一些其他的公式使用率并不是那么高,如果会用到,可以查阅相关资料。
7.索引、切片和迭代
一维数组的切片方式和Python列表基本相似。
我们直接可以通过:
数 组 名 [ 索 引 号 ] 数组名[索引号] 数组名[索引号] 的方式进行索引
数 组 名 [ 起 始 索 引 : 结 束 索 引 : 索 引 间 隔 ] 数组名[起始索引:结束索引:索引间隔] 数组名[起始索引:结束索引:索引间隔] 的方式进行切片,若不填写起始索引和结束索引,则认为是到最开始和最末尾;若不填写索引间隔,则默认为1
可以使用 f o r for for循环进行迭代
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a[3] # 取索引为3的元素
3
>>> a[2:8] # 取索引为2-8的元素,不包括8
array([2, 3, 4, 5, 6, 7])
>>> a[::3] # 每3个索引取一次
array([0, 3, 6, 9])
>>> for i in a:
... print(i,end=" ")
0 1 2 3 4 5 6 7 8 9
索引时也可以使用一定的条件进行索引
>>> a[a>5]
array([6, 7, 8, 9])
多维数组的的每一个维度有一个索引,它们可以用元组表示
可以使用
数 组 名 [ 一 维 索 引 ] [ 二 维 索 引 ] . . . [ n 维 索 引 ] 数组名[一维索引][二维索引]...[n维索引] 数组名[一维索引][二维索引]...[n维索引]的方式进行索引
而在进行切片时,可以对每一个维度进行如同一维数组一样的索引
数 组 名 [ ( 一 维 ) 起 始 索 引 : 结 束 索 引 : 索 引 间 隔 , ( 二 维 ) 起 始 索 引 : 结 束 索 引 : 索 引 间 隔 , . . . , ( n 维 ) 起 始 索 引 : 结 束 索 引 : 索 引 间 隔 ] 数组名[(一维)起始索引:结束索引:索引间隔,(二维)起始索引:结束索引:索引间隔,...,(n维)起始索引:结束索引:索引间隔] 数组名[(一维)起始索引:结束索引:索引间隔,(二维)起始索引:结束索引:索引间隔,...,(n维)起始索引:结束索引:索引间隔]
直接看下面的例子:
>>> def f(x, y):
... return 5*x+y
>>> a = np.fromfunction(f,(4,4),dtype = np.int64
>>> # 从函数建立数组,x和y分别为索引的值
array([[ 0, 1, 2, 3],
[ 5, 6, 7, 8],
[10, 11, 12, 13],
[15, 16, 17, 18]], dtype=int64)
>>> a[3,2]
17
>>> a[:,1:3]
array([[ 1, 2],
[ 6, 7],
[11, 12],
[16, 17]], dtype=int64)
需要注意的是如果在索引中传入-1,则会显示最后一个元素或最后一列/行
>>> a[1][-1]
8
在迭代时,多维数组对第一个维度进行迭代,如果我们想迭代元素,则可以使用 f l a t flat flat进行扁平化处理
>>> for row in a:
... print(row)
[0 1 2 3]
[5 6 7 8]
[10 11 12 13]
[15 16 17 18]
>>> for elm in a.flat:
... print(elm,end=" ")
0 1 2 3 5 6 7 8 10 11 12 13 15 16 17 18
8.数组的反转
数组可以进行一些特殊的变化操作,下面直接进行演示
>>> a = np.random.randint(8,size=(2,4))
>>> a
array([[3, 7, 7, 5],
[6, 6, 1, 7]])
>>> a.shape
(2, 4)
>>> a.ravel() # 扁平化处理 也可以使用flatten()
array([3, 7, 7, 5, 6, 6, 1, 7])
>>> a.flatten()
array([3, 7, 7, 5, 6, 6, 1, 7])
>>> a.T # 对数组进行转置
array([[3, 6],
[7, 6],
[7, 1],
[5, 7]])
''' reshape和resize的区别在于 resize会改变当前变量的形状 而reshape则不会 '''
>>> a.resize((2,4))
>>> a
array([[3, 7, 7, 5],
[6, 6, 1, 7]])
>>> a.reshape(1,8)
array([[3, 7, 7, 5, 6, 6, 1, 7]])
>>> a
array([[3, 7, 7, 5],
[6, 6, 1, 7]])
如果已经确定了形状的其中一个参数,那么另一个参数可以设为-1,会自动计算出这个值是多少
>>> a = np.randint(1000,size = (10*100))
>>> b = a.reshape(25,-1)
>>> b.shape
(25, 40)
8.数组的堆叠
Numpy可以把一些数组从不同的方向进行堆叠
>>> a = np.zeros((2,2))
>>> b = np.ones((2,2))
>>> np.vstack((a,b)) # 列堆叠
array([[0., 0.],
[0., 0.],
[1., 1.],
[1., 1.]])
>>> np.hstack((a,b)) # 行堆叠
array([[0., 0., 1., 1.],
[0., 0., 1., 1.]])
9.数组的切分
通过使用hsplit,可以把一个较大的数组在水平方向上切分成为比较小的数组,并且放回指定大小的数组
>>> a = np.random.randint(20,size=(2,10))
>>> a
array([[17, 0, 4, 16, 0, 11, 1, 0, 7, 7],
[ 8, 9, 4, 0, 15, 5, 16, 3, 1, 16]])
>>> np.hsplit(a,2) # 将a数组分为两个数组
[array([[17, 0, 4, 16, 0],
[ 8, 9, 4, 0, 15]]),
array([[11, 1, 0, 7, 7],
[ 5, 16, 3, 1, 16]])]
>>> np.hsplit(a,(2,5)) # 从2和5处分割a数组
[array([[17, 0],
[ 8, 9]]),
array([[ 4, 16, 0],
[ 4, 0, 15]]),
array([[11, 1, 0, 7, 7],
[ 5, 16, 3, 1, 16]])]
和这个类似的,vsplit()和hsplit()的方式相同,只不过是沿垂直轴进行拆分。而array_split()需要用户指定要沿哪个轴进行拆分。
>>> a = np.random.randint(48,size=(6,8))
>>> a
array([[29, 14, 16, 44, 35, 4, 13, 18],
[12, 31, 15, 6, 12, 45, 3, 41],
[28, 11, 29, 3, 31, 20, 29, 41],
[30, 1, 21, 21, 13, 2, 45, 6],
[43, 47, 0, 41, 41, 23, 38, 38],
[16, 3, 18, 28, 43, 45, 38, 1]])
>>> np.vsplit(a,2)
[array([[29, 14, 16, 44, 35, 4, 13, 18],
[12, 31, 15, 6, 12, 45, 3, 41],
[28, 11, 29, 3, 31, 20, 29, 41]]),
array([[30, 1, 21, 21, 13, 2, 45, 6],
[43, 47, 0, 41, 41, 23, 38, 38],
[16, 3, 18, 28, 43, 45, 38, 1]])]
>>> np.array_split(a,(2,5),axis=0)
[array([[29, 14, 16, 44, 35, 4, 13, 18],
[12, 31, 15, 6, 12, 45, 3, 41]]),
array([[28, 11, 29, 3, 31, 20, 29, 41],
[30, 1, 21, 21, 13, 2, 45, 6],
[43, 47, 0, 41, 41, 23, 38, 38]]),
array([[16, 3, 18, 28, 43, 45, 38, 1]])]
10.数组的复制
在复制这里分为三种情况:无复制,浅复制和深复制
(1)无复制
>>> a = np.array([[1,2],[3,4]])
>>> b = a # 并没有新的对象产生
>>> b is a # a和b只是一个数组类的名称
True
(2)浅复制
不同的数组对象可以共享相同的数据,view()方法提供了一个创建这样一个数组的可能
>>> c = a.view()
>>> c
array([[1, 2],
[3, 4]])
>>> c is a
False
>>> c.base is a
True
>>> c = c.reshape((1, 4))
>>> c.shape
(1, 4)
>>> a.shape # a的形状并没有发生改变
(2, 2)
>>> c[0,0]=666
>>> a # a的数据发生了变化
array([[666, 2],
[ 3, 4]])
(3)深复制
Numpy提供的copy()方法可以做到一个完全的复制。
直接看例子
>>> d = a.copy()
>>> d is a # d和a是两个对象
False
>>> d.base is a # d和a不共享任何数据
False
>>> d[0][0] = 999
>>> a # a中的值没有发生变化
array([[666, 2],
[ 3, 4]])
有些时候,我们在复制过一个切分好后的数组时,原始数组已经没有了价值,故可以直接删除即可
>>> e = a[:,1].copy()
>>> del a
11.广播(Broadcasting)
广播的机制可以使得一些输入形状不完全相同的数组在进行以上操作时变得有意义。广播机制有以下几条规则:
a. 让所有输入数组都向其中形状最长的数组看齐,形状中不足的部分都通过在前面加 1 补齐。
b. 输出数组的形状是输入数组形状的各个维度上的最大值。
c. 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时,这个数组能够用来计算,否则出错。
d. 当输入数组的某个维度的长度为 1 时,沿着此维度运算时都用此维度上的第一组值。
简而言之,广播会将无法计算的数组扩充为可以计算的数组
>>> a = np.array([[ 0, 0, 0],[10,10,10]])
>>> b = np.array([1,2,3])
>>> a + b
array([[ 1, 2, 3],
[11, 12, 13]])
*12.进阶索引和索引技巧
(1)数组做数组的索引
数组可以作为一个数组的索引,直接看举例
>>> a = np.arange(10)**2 # 前十个平方数的数组
>>> a
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81], dtype=int32)
>>> index = np.array([1,3,4,6]) # 定义一个索引数组
>>> a[index]
array([ 1, 9, 16, 36], dtype=int32)
>>> j = np.array([[3, 4], [9, 7]]) # 定义一个二维索引数组
>>> a[j] # 得到的结果与j数组的形状一致
array([[ 9, 16],
[81, 49]], dtype=int32)
(2)布尔元素类型的数组
布尔类型的数组可以作为另一个同形状数组的索引,如果索引为True,则输出,如果索引为False,则不输出。
>>> a = np.arange(12).reshape(3,4)
>>> b = a > 6
>>> b
array([[False, False, False, False],
[False, False, False, True],
[ True, True, True, True]])
>>> a[b]
array([ 7, 8, 9, 10, 11])
边栏推荐
- Chain team implementation (C language)
- The most popular colloquial system explains the base of numbers
- 【指针】求解最后留下的人
- SQL注入
- 【指针】数组逆序重新存放后并输出
- Internet Management (Information Collection)
- XSS unexpected event
- Statistics, 8th Edition, Jia Junping, Chapter 6 Summary of knowledge points of statistics and sampling distribution and answers to exercises after class
- servlet中 servlet context与 session与 request三个对象的常用方法和存放数据的作用域。
- “人生若只如初见”——RISC-V
猜你喜欢

Network technology related topics
High concurrency programming series: 6 steps of JVM performance tuning and detailed explanation of key tuning parameters

Wu Enda's latest interview! Data centric reasons

JDBC事务、批处理以及连接池(超详细)
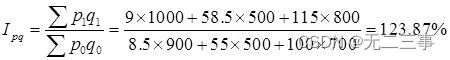
《统计学》第八版贾俊平第十四章指数知识点总结及课后习题答案
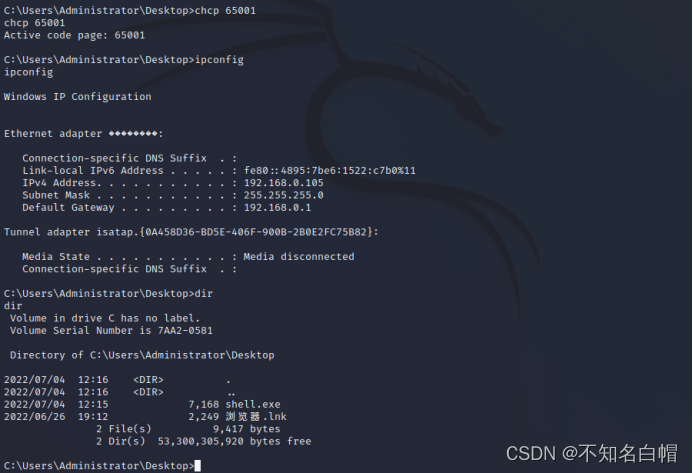
Intranet information collection of Intranet penetration (I)
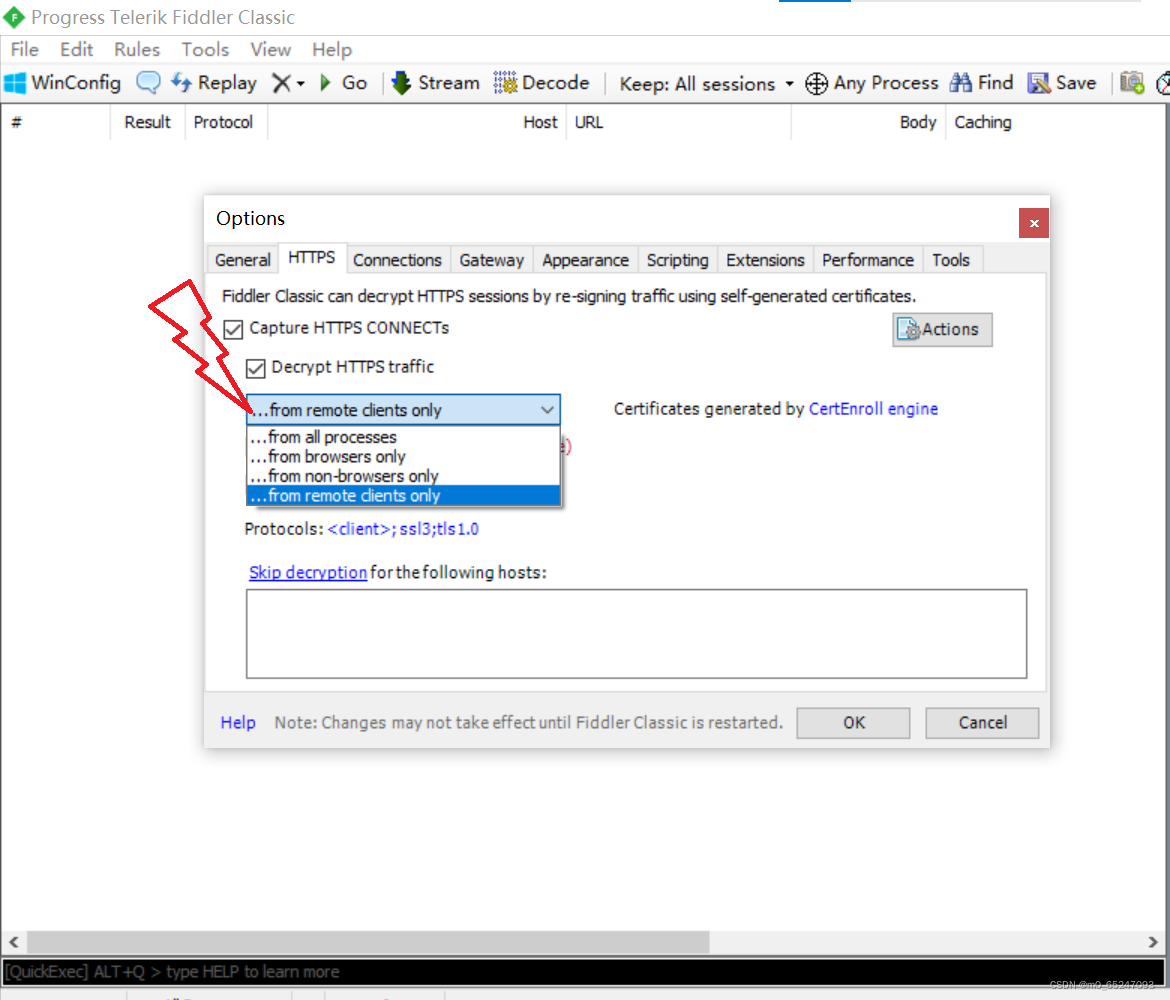
Applet Web Capture -fiddler

SystemVerilog discusses loop loop structure and built-in loop variable I

《統計學》第八版賈俊平第七章知識點總結及課後習題答案
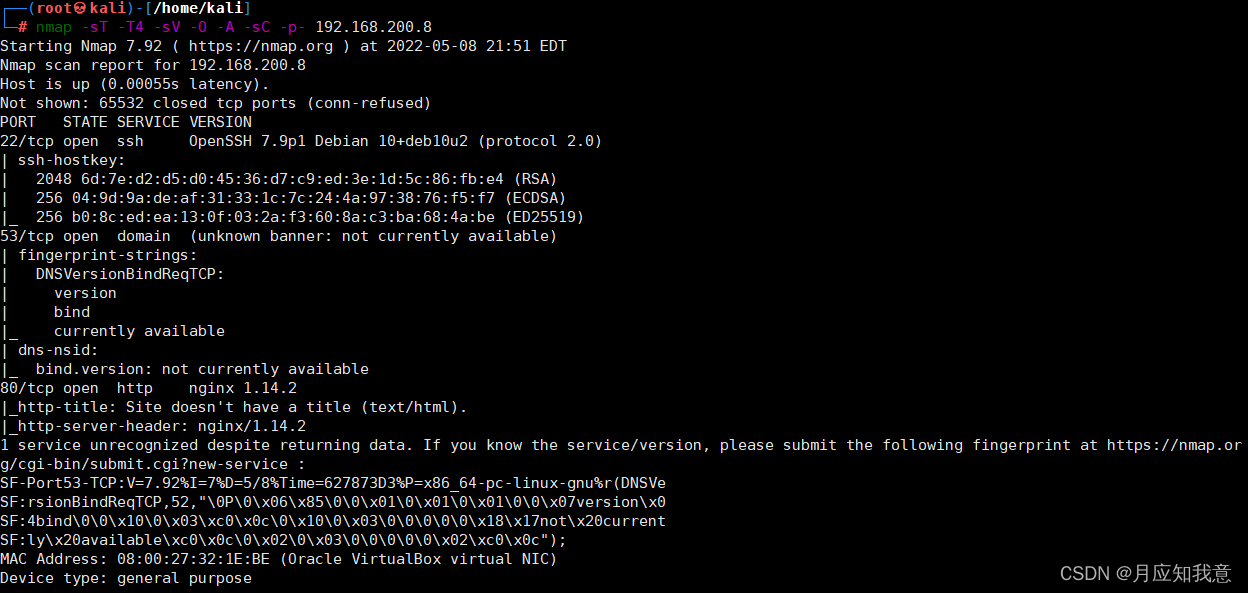
Hackmyvm target series (1) -webmaster
随机推荐
Statistics 8th Edition Jia Junping Chapter 7 Summary of knowledge points and answers to exercises after class
Detailed explanation of network foundation
XSS (cross site scripting attack) for security interview
小程序web抓包-fiddler
How to understand the difference between technical thinking and business thinking in Bi?
网络层—简单的arp断网
Xray and Burp linked Mining
《统计学》第八版贾俊平第四章总结及课后习题答案
Hackmyvm target series (2) -warrior
Hcip -- MPLS experiment
《统计学》第八版贾俊平第九章分类数据分析知识点总结及课后习题答案
Feature extraction and detection 14 plane object recognition
《統計學》第八版賈俊平第七章知識點總結及課後習題答案
Interpretation of iterator related "itertools" module usage
Résumé des points de connaissance et des réponses aux exercices après la classe du chapitre 7 de Jia junping dans la huitième édition des statistiques
XSS unexpected event
New version of postman flows [introductory teaching chapter 01 send request]
Load balancing ribbon of microservices
C language file operation
内网渗透之内网信息收集(二)