当前位置:网站首页>Statistics 8th Edition Jia Junping Chapter 5 probability and probability distribution
Statistics 8th Edition Jia Junping Chapter 5 probability and probability distribution
2022-07-06 14:29:00 【No two or three things】
One 、 Examination site induction
Two 、 Exercises 1 Write the sample space for the following randomized trials :
(1) Record the average score of a statistical test in a class ;
(2) Someone is riding a bike on the road , Observe the number of times the cyclist meets the green light before stopping at the first red light ;
(3) Produce products until 10 Until it is genuine , Record the total number of products produced .
Explain :(1) The average score is in the range 0~100 A continuous variable between , So the sample space of the average score Ω=[0,100].
(2) The number of green lights encountered is from 0 Any natural number at the beginning , So sample space Ω=N.
(3) There may be no defective products or any number of defective products in the products previously produced , So sample space Ω={10,11,12,13,…}.
2 Someone's flower 2 Yuan to buy lottery , He hit 100 The probability of a yuan prize is 0.1%, win a lottery 10 The probability of a yuan prize is 1%, win a lottery 1 The probability of a yuan prize is 20%, Suppose all kinds of prizes cannot be won at the same time , Try to ask for :
(1) The probability distribution of this person's income .
(2) The expected value of this person's income .
Explain :(1) set up X For the benefit of this person , win a lottery 100 The income of yuan prize is 100-2=98( element ), win a lottery 10 The income of yuan prize is 10-2=8( element ), win a lottery 1 When you win a prize, you will lose 1 element , win a lottery 0 When you win a prize, you will lose 2 element , Then the probability distribution of this person's income is :
P(X=98)=0.001
P(X=8)=0.01
P(X=-1)=0.2
P(X=-2)=1-P(X=98)-P(X=8)-P(X=-1)=0.789
(2)E(X)=98×0.001+8×0.01+(-1)×0.2+(-2)×0.789=1.6
3 Set the random variable X The probability density of is :
f(x)=3x2/θ3,0<x<θ
(1) It is known that P(X>1)=7/8, seek θ Value .
(2) seek X Expectation and variance of .
Explain :(1) from P(X>1)=7/8 Available :P(X≤1)=1-P(X>1)=1/8, namely
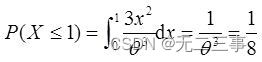
Solution :θ=2. therefore , A random variable X The probability density of is :f(x)=3x2/8,0<x<2.
(2) from X The expected value of the probability density is :
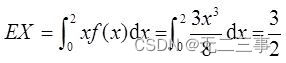
also
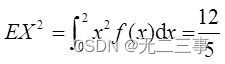
therefore
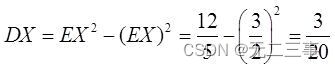
4 There is 5 questions , At the same time, each question lists 4 An alternative answer , One of the answers is correct . A student can answer correctly by guessing at least 4 What's the probability of the problem ?
Explain : set up X Is the number of correct answers . From the meaning of the question , The probability of answering a question correctly is 1/4. that X~B(5,1/4), So the answer is right, at least 4 The probability of the problem is :
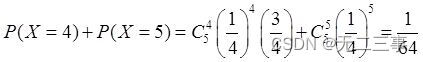
5 Set the random variable X The compliance parameter is λ The Poisson distribution of , And known P{X=1}=P{X=2}, seek P{X=4}. Explain : The formula of Poisson distribution has :
P(X=1)=λe-λ
P(X=2)=λ2e-λ/(2!)
from P{X=1}=P{X=2}, Solution :λ=2.
therefore P(X=4)=24×e-2÷4!=2/(3e2).
6 set up X~N(3,4), Try to ask for :(1)P{|X|>2};(2)P{X>3}.
Explain :(1)
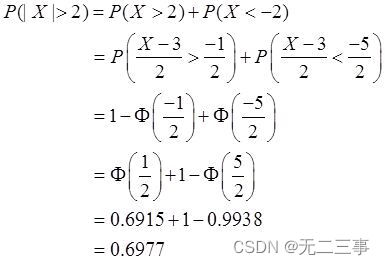
(2) because N(3,4) About the mean 3 symmetry , therefore P{X>3}=1/2.
7 The life of electronic tubes produced by a factory X( In hours ) Obey expectations μ=160 Is a normal distribution , If required P{120<X<200}≥0.08, Allowable standard deviation σ What is the maximum ?
Explain : from
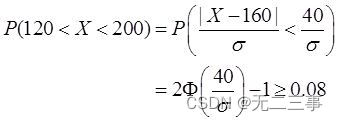
Available :Φ(40/σ)≥0.54, Look up the table :40/σ≥0.1004, so σ≤398.41. That is, the allowable standard deviation σ The maximum is 398.41.8 The number of errors in the proofreading of a book after typesetting X It follows a normal distribution N(200,400), seek :
(1) The number of errors does not exceed 230 Probability .
(2) The number of errors is 190~210 Probability between .
Explain :(1) The number of errors does not exceed 230 The probability of is :
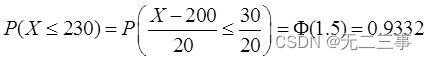
(2) The number of errors is 190~210 The probability between is :
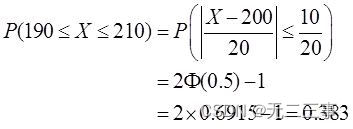
边栏推荐
- Captcha killer verification code identification plug-in
- Strengthen basic learning records
- A complete collection of papers on text recognition
- XSS之冷门事件
- MSF generate payload Encyclopedia
- Lintcode logo queries the two nearest saplings
- [experiment index of educator database]
- Attach the simplified sample database to the SQLSERVER database instance
- Callback function ----------- callback
- Hcip -- MPLS experiment
猜你喜欢
循环队列(C语言)
Hackmyvm target series (4) -vulny

Low income from doing we media? 90% of people make mistakes in these three points
Attack and defense world misc practice area (simplerar, base64stego, no matter how high your Kung Fu is, you are afraid of kitchen knives)
HackMyvm靶机系列(3)-visions
How does SQLite count the data that meets another condition under the data that has been classified once

Strengthen basic learning records

《英特尔 oneAPI—打开异构新纪元》
中间件漏洞复现—apache
How to earn the first pot of gold in CSDN (we are all creators)
随机推荐
中间件漏洞复现—apache
小程序web抓包-fiddler
图书管理系统
7-7 7003 combination lock (PTA program design)
Experiment five categories and objects
Interpretation of iterator related "itertools" module usage
The difference between layer 3 switch and router
AQS details
Chain team implementation (C language)
How to turn wechat applet into uniapp
7-8 7104 Joseph problem (PTA program design)
HackMyvm靶机系列(4)-vulny
Sqqyw (indifferent dot icon system) vulnerability recurrence and 74cms vulnerability recurrence
Applet Web Capture -fiddler
内网渗透之内网信息收集(四)
Record an edu, SQL injection practice
Network layer - simple ARP disconnection
Attach the simplified sample database to the SQLSERVER database instance
Attack and defense world misc practice area (GIF lift table ext3)
Realize applet payment function with applet cloud development (including source code)