《统计学》第八版贾俊平第四章总结及课后习题答案

1.考点归纳

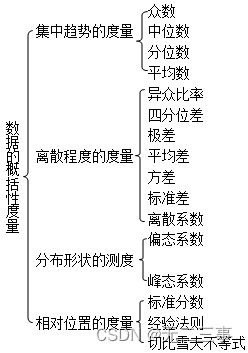
2.考点提示

（1）集中趋势、离散趋势的度量指标，包括每个指标的含义、计算公式、特点、意义、适用范围（选择题、简答题、计算题考点）；
（2）众数、中位数和平均数三个指标的特点和应用场合，偏态分布下三个指标的关系（选择题、简答题、计算题考点）；
（3）分布形状的测度指标：偏态系数和峰态系数的数值含义（选择题、简答题考点）。
（4）标准分数的计算公式及应用（选择题、简答题、计算题考点）；
（5）经验法则、切比雪夫不等式的具体应用（选择题考点）。

3.考点核心

（1）：集中趋势的度量
 

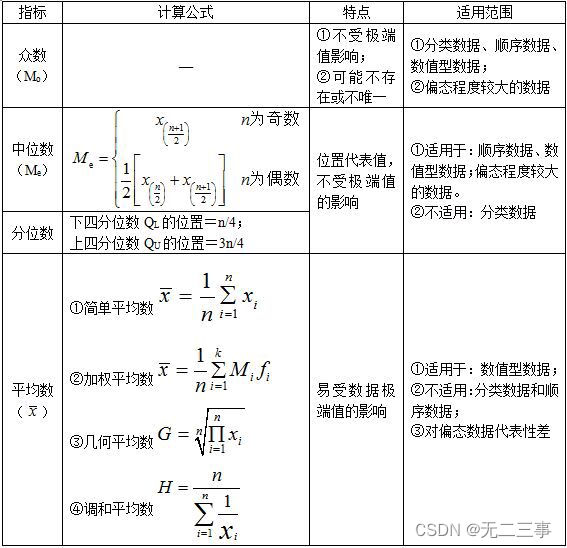
【注意】不同偏态程度的分布中集中趋势度量指标的关系：①对称分布中，众数、中位数和平均数相等；②左偏分布中，数据存在极小值，拉动平均数向极小值一方靠，而众数和中位数不受极值的影响，有x＜Me＜Mo；③右偏分布中，数据存在极大值，必然拉动平均数向极大值一方靠，因此Mo＜Me＜x。

(2)离散程度的度量
数据的离散程度反映了各变量值远离其中心值的程度，离散程度越小，代表性就越好。

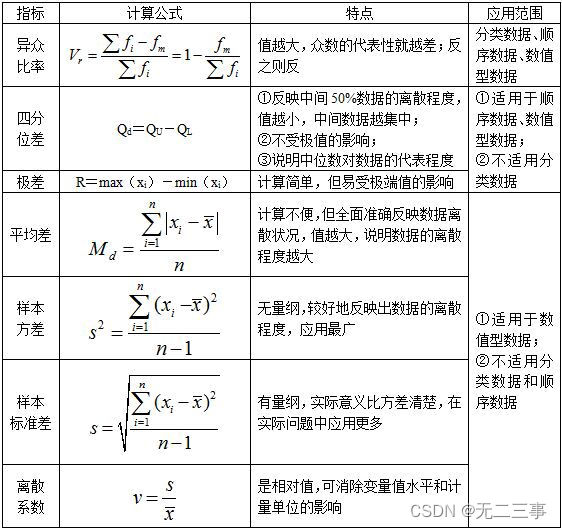
(3)分布形状的测度
偏态是对数据分布对称性的测度，峰态是对数据分布平峰或尖峰程度的测度。
 

(4)相对位置的度量
（1）标准分数（标准化值或z分数）

①计算公式：zi＝（xi－x）/s。

②特点：平均数为0、标准差为1；对数据进行了线性变换，不改变数据在该组数据中的位置，也不改变该组数据分布的形状。

③用途：
a．测定某一数据在该组数据中的相对位置，并可以用它来判断一组数据是否有离群数据；
b．处理多个具有不同量纲的变量时，标准分数可用于对各变量进行标准化处理。
（2）经验法则（3σ原则）
当一组数据对称分布时，经验法则表明：

①约有68%的数据在平均数±1个标准差的范围之内；

②约有95%的数据在平均数±2个标准差的范围之内；

③约有99%的数据在平均数±3个标准差的范围之内。
因此，在平均数±3个标准差的范围内几乎包含了全部数据，而在±3个标准差之外的数据称为离群点。
（3）切比雪夫不等式

①概念：对于任意分布形态的数据，根据切比雪夫不等式，至少有（1－1/k2）的数据落在±k个标准差之内。其中k是大于1的任意值，不一定是整数。对于k＝2，3，4，该不等式的含义是：
a．至少有75%的数据落在平均数±2个标准差的范围之内；
b．至少有89%的数据落在平均数±3个标准差的范围之内；
c．至少有94%的数据落在平均数±4个标准差的范围之内。

②特点：切比雪夫不等式对任何分布形状的数据都适用。

二练习题

1一家汽车零售店的10名销售人员5月份销售的汽车数量（单位：台）排序后如下：
2　4　7　10　10　10　12　12　14　15
要求：
（1）计算汽车销售量的众数、中位数和平均数。
（2）根据定义公式计算四分位数。
（3）计算销售量的标准差。
（4）说明汽车销售量分布的特征。

解：（1）10名销售人员5月份销售的汽车数量中，销售10台汽车的人数最多，为3人，因此众数M0＝10。
中位数位置＝（n＋1）/2＝（10＋1）/2＝5.5，所以Me＝（10＋10）/2＝10（台）。
平均数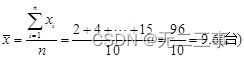
（2）由题中数据可得：

①QL位置＝n/4＝10/4＝2.5，即QL在第2个数值（4）和第3个数值（7）之间0.5的位置上。因此
QL＝（4＋7）/2＝5.5（台）

②QU位置＝3n/4＝3×10÷4＝7.5，即QU在第7个数值（12）和第8个数值（12）之间0.5的位置上，因此
QU＝（12＋12）/2＝12（台）

（3）由平均数x＝9.6可得：

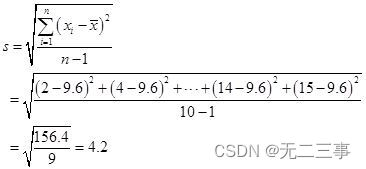
（4）由于平均数小于中位数和众数，所以汽车销售量为左偏分布。

2随机抽取25个网络用户，得到他们的年龄数据如表4-4所示。

要求：
（1）计算众数、中位数。
（2）计算四分位数。

（3）计算平均数和标准差。
（4）计算偏态系数和峰态系数。
（5）对网民年龄的分布特征进行综合分析。

解：（1）对表4-4中数据按从小到大顺序排列：

由排序数据可知，年龄出现频数最多的是19和23，都出现3次，所以有两个众数，即Mo＝19和Mo＝23。
由于中位数位置＝（n＋1）/n＝（25＋1）/2＝13，所以Me＝23（岁）
（2）由题中数据可计算四分位数：

①QL位置＝n/4＝25/4＝6.25，即QL在第6个数值（19）和第7个数值（19）之间0.25的位置上，因此

QL＝19＋0.25×（19－19）＝19（岁）

②由于QU位置＝3×25/4＝25/4＝18.75，即QU在第18个数值（25）和第19个数值（27）之间0.75的位置上，因此
QU＝25＋0.75×（27－25）＝26.5（岁）
（3）平均数

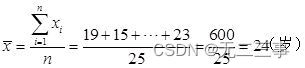
由平均数x＝24可得：

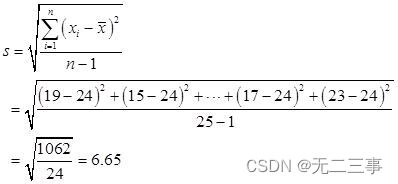
（4）偏态系数：

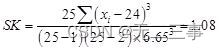
峰态系数：

（5）对网民年龄的分布特征进行综合分析的结果如下：从众数、中位数和平均数来看，网民年龄在23岁左右的人占多数；标准差较大，说明网民之间的年龄差异较大；偏态系数大于1，表明网民的年龄分布为右偏，且偏斜程度很大。峰态系数为正值，是尖峰分布，表明网民的年龄分布较为集中。

3某电商6月份各天的销售额数据

要求：
（1）计算该百货公司日销售额的平均数和中位数。
（2）计算四分位数。
（3）计算日销售额的标准差。

解：（1）由日销售额的平均数为：

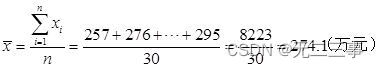
将表4-5中数据排序可得：

中位数位置＝（30＋1）/2＝15.5，因此Me＝（272＋273）/2＝272.5
（2）由题中数据可计算四分位数：

①由于QL位置＝30/4＝7.5，即QL在第7个数值（258）和第8个数值（261）之间0.5的位置上。因此

QL＝（258＋261）/2＝259.5（万元）②QU位置＝3×30÷4＝22.5，即QL在第22个数值（284）和第23个数值（291）之间0.5的位置上。因此
QU＝（284＋291）/2＝287.5（万元）
（3）由日销售额的平均数x＝274.1可得：

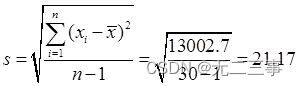
4在某地区抽取120家企业，按利润额进行分组。

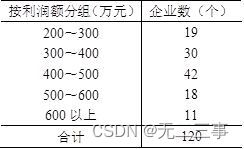
要求：

（1）计算120家企业利润额的平均数和标准差。
（2）计算分布的偏态系数和峰态系数。

解：（1）平均数计算过程如表4-7所示。
表4-7　某地区120家企业利润额平均数计算过程表

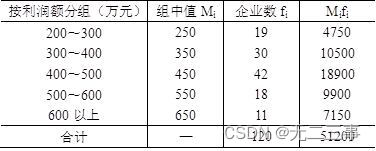
由表4-7中数据可得平均数：

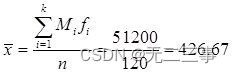
标准差计算过程如表4-8所示。

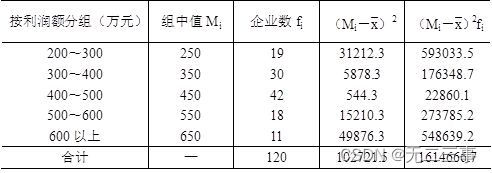
表4-8　某地区120家企业利润额标准差计算过程表

由表4-8中数据可得：

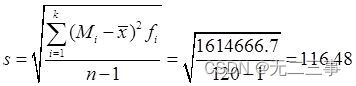
（2）偏态系数和峰态系数的计算过程如表4-9所示。
表4-9　偏态系数和峰态系数计算过程表

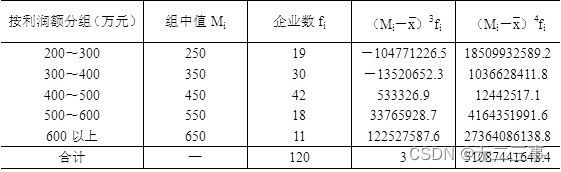
由表中数据可得偏态系数为：

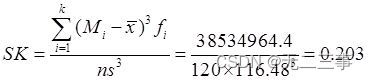
由表中数据可得峰态系数：

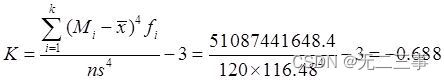
5一条产品生产线平均每天的产量为3700件，标准差为50件。如果某一天的产量低于或高于平均产量，并落入±2个标准差的范围之外，就认为该生产线“失去控制”。表4-10是一周各天的产量，该生产线哪几天失去了控制？
表4-10　产品生产线产量资料

解：由于x＝3700，s＝50，利用公式zi＝（xi－x）/s可以计算每天的标准分数，如表4-11所示。

表4-11　产品生产线产量的标准分数表
由表4-11中数据可知：周一、周六的标准分数的绝对值大于2，所以周一和周六两天失去了控制。

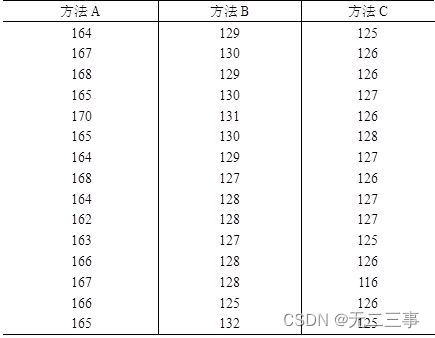
6一种产品需要人工组装，现有三种可供选择的组装方法。为检验哪种方法更好，随机抽取15个工人，让他们分别用三种方法组装。表4-12是15个工人分别用三种方法在相同的时间内组装的产品数量。
表4-12　工人用三种方法在相同的时间内组装的产品数量（单位：个）

要求：
（1）你准备采用什么方法来评价组装方法的优劣？

（2）如果让你选择一种方法，你会作出怎样的选择？试说明理由。解：（1）应该从平均数和标准差两个方面进行评价。在对各种方法的离散程度进行比较时，应该采用离散系数。
（2）表4-13给出了用Excel计算一些主要描述统计量。
表4-13　描述统计量

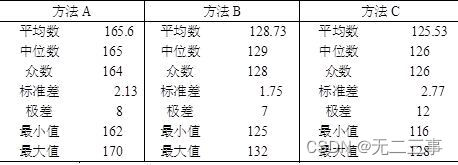
从三种方法的集中趋势来看，方法A的平均产量最高，中位数和众数也都高于其他两种方法。从离散程度来看，三种方法的离散系数分别为：
vA＝sA/xA＝2.13/165.6＝0.013

vB＝sB/xB＝1.75/128.73＝0.014
vA＝sC/xC＝2.77/125.53＝0.022
方法A的离散系数最小，即离散程度最小，因此应选择方法A。