Résumé des points de connaissance et des réponses aux exercices après la classe du chapitre 7 de Jia junping dans la huitième édition des statistiques

Un..Résumé des points d'examen

Justification de l'estimation des paramètres

1Intervalle de confiance
（1）Le niveau de confiance est95%Signification de l'intervalle de confiance pour：Tous les intervalles construits d'une manière ou d'une autre ont95%L'intervalle pour contient la valeur réelle du paramètre global.（2）Plus la confiance est élevée（C'est - à - dire que plus la fiabilité de l'estimation est élevée）,L'intervalle de confiance est donc plus large（Plus l'exactitude des estimations est faible）.
（3）Caractéristiques des intervalles de confiance：L'intervalle de confiance est influencé par l'échantillon,Aléatoire,La valeur réelle du paramètre global est fixe.Un intervalle de confiance spécifique“Toujours inclure”Ou“Absolument pas”La vraie valeur du paramètre,N'existe pas“Quelle est la probabilité d'inclure les paramètres globaux”La question de.

2Critères d'évaluation des estimations
（1）Non biaisé：Estimation la valeur attendue de la distribution de l'échantillon est égale au paramètre de population estimé,C'est - à - dire:E（θ）＝θ.
（2）Efficacité：La variance de l'estimation est aussi faible que possible.
（3）Cohérence：À mesure que la taille de l'échantillon augmente,Les estimations sont de plus en plus proches des paramètres de la population estimée.

Estimation de l'intervalle d'un paramètre global

2.、 Exercices et réponses après la classe

1 Utiliser les informations suivantes , Construire des intervalles de confiance pour la moyenne globale .
（1）La population suit une distribution normale,Et connu pourσ＝500,n＝15,x＝8900,Le niveau de confiance est95%.
（2） Distribution normale de la désobéissance générale ,Et connu pourσ＝500,n＝35,x＝8900,Le niveau de confiance est95%.
（3） Distribution normale de la désobéissance générale ,σInconnu,n＝35,x＝8900,s＝500,Le niveau de confiance est90%.
（4） Distribution normale de la désobéissance générale ,σInconnu,n＝35,x＝8900,s＝500,Le niveau de confiance est99%.

Solution：（1） Parce que la population suit une distribution normale ,σ＝500,n＝15,x＝8900,α＝0.05,z0.05/2＝1.96. Donc la moyenne globale μDe95%L'intervalle de confiance pour：

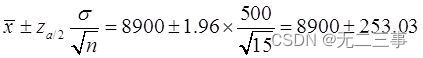
C'est - à - dire:（8646.97,9153.03）.
（2） Population connue non conforme à la distribution normale ,Mais...n＝35 Pour un grand échantillon ,AdoptionzStatistiques,Moyenne globaleμDe95%L'intervalle de confiance pour：

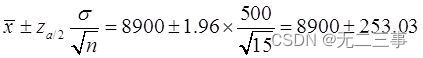
C'est - à - dire:（8734.35,9065.65）.
（3） Population connue non conforme à la distribution normale ,σInconnu,Mais parce quen＝35 Pour un grand échantillon ,Il est donc possible d'adopterzStatistiques,Moyenne globaleμDe90%L'intervalle de confiance pour：

C'est - à - dire:（8760.97,9039.03）.
（4） Population connue non conforme à la distribution normale ,σInconnu,Mais parce quen＝35 Pour un grand échantillon ,Il est donc possible d'adopterzStatistiques,Moyenne globaleμDe99%L'intervalle de confiance pour：

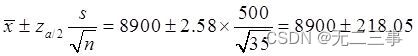
C'est - à - dire:（8681.95,9118.05）.

2 Une université veut savoir quand les étudiants surfent sur Internet tous les jours ,Dans toute l'école7500 Échantillonnage répété parmi les élèves 36Les gens, Vérifiez combien de temps ils passent en ligne tous les jours. ,Prends le tableau.7-3Données（Unité：Heures）.

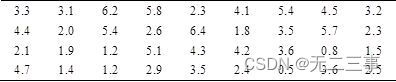
Intervalle de confiance pour le temps moyen d'accès à Internet des étudiants de l'université , Les niveaux de confiance sont les suivants: 90%,95%Et99%.

Solution：Connu pour：n＝36,QuandαPour0.1,0.05,0.01Heure,CorrespondantzLes valeurs sont:：z0.1/2＝1.645,z0.05/2＝1.96,z0.01/2＝2.58
Calculé à partir des données de l'échantillon ：

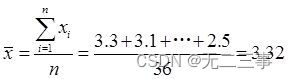
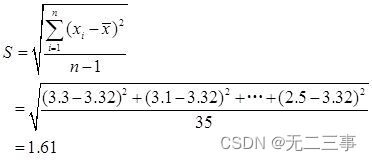
（1）Parce quen＝36 Pour un grand échantillon , Donc le temps moyen en ligne 90%L'intervalle de confiance pour：

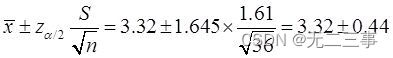
C'est - à - dire:（2.88,3.76）.
（2） Temps moyen d'accès à Internet 95%L'intervalle de confiance pour：

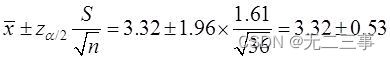
C'est - à - dire:（2.79,3.85）.
（3） Temps moyen d'accès à Internet 99%L'intervalle de confiance pour：

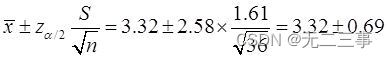
C'est - à - dire:（2.63,4.01）.

3 Les aliments ensachés produits par une entreprise sont emballés par une machine d'emballage automatique , Poids standard par sac 100g, Un échantillon aléatoire est prélevé sur un lot de produits fabriqués un jour par échantillonnage répété. 50 Inspection des colis , Le poids de chaque colis mesuré est indiqué dans le tableau. .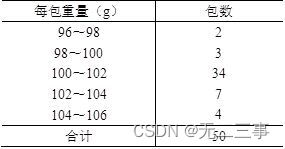

Le poids de l'emballage alimentaire est connu de la distribution normale ,Exigences：
（1） Pour déterminer le poids moyen de cet aliment 95%Intervalle de confiance pour.
（2） Si le poids de l'aliment spécifié est inférieur à 100g Non qualifié , Pour déterminer le taux de qualification de ce lot de denrées alimentaires 95%Intervalle de confiance pour.

Solution：（1）Connu pour：La population suit une distribution normale,Mais...σInconnu,n＝50 Pour un grand échantillon ,α＝0.05,z0.05/2＝1.96. Calculé à partir des données de l'échantillon groupé ：x＝（97×2＋99×3＋…＋105×4）/50＝101.32

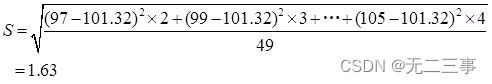
Poids moyen de cet aliment 95%L'intervalle de confiance pour：

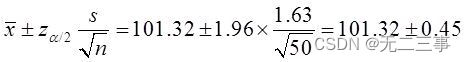
C'est - à - dire:（100.87,101.77）.
（2） Selon les données de l'échantillon , Le taux de réussite de l'échantillon est le suivant: p＝45/50＝0.9. Taux de qualification 95%L'intervalle de confiance pour：

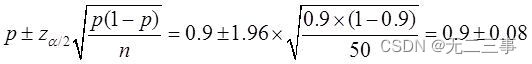
C'est - à - dire:（0.82,0.98）.

4 Supposons que la population suive une distribution normale ,Tableau d'utilisation7-5 Moyenne globale de la construction des données pour μDe99%Intervalle de confiance pour.

Solution：Connu pour：La population suit une distribution normale,Mais...σInconnu,n＝25 Pour les petits échantillons ,α＝0.01,t0.01/2（25－1）＝2.797. Calculé à partir des données de l'échantillon ：x＝16.128,s＝0.871. Moyenne globale μDe99%L'intervalle de confiance pour：

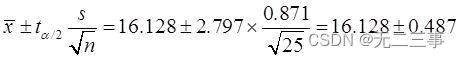
C'est - à - dire:（15.64,16.62）.

5 Construire des proportions globales à l'aide des données de l'échantillon ci - dessous πIntervalle de confiance pour.
（1）n＝44,p＝0.51,Le niveau de confiance est99%.
（2）n＝300,p＝0.82,Le niveau de confiance est95%.
（3）n＝1150,p＝0.48,Le niveau de confiance est90%.

Solution：（1）Connu pour：n＝44,p＝0.51,α＝0.01,z0.01/2＝2.58.Proportion globaleπDe99%L'intervalle de confiance pour：

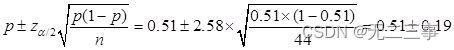
C'est - à - dire:（0.32,0.70）.
（2）Connu pour：n＝300,p＝0.82,α＝0.05,z0.05/2＝1.96.Proportion globaleπDe95%L'intervalle de confiance pour：

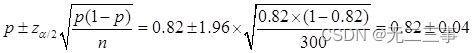
C'est - à - dire:（0.78,0.86）.
（3）Connu pour：n＝1150,p＝0.48,α＝0.1,z0.1/2＝1.645.Proportion globaleπDe90%L'intervalle de confiance pour：

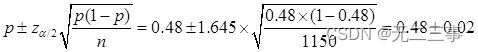
C'est - à - dire:（0.46,0.50）.

6 Dans une étude de marché sur les appareils ménagers , Au hasard. 200 Ménages , Vérifier s'ils possèdent une marque de télévision . Les ménages qui possèdent des téléviseurs de marque 23%. Trouver l'intervalle de confiance pour la proportion globale , Les niveaux de confiance sont les suivants: 90%Et95%.Solution：Connu pour：n＝200,p＝0.23,αPour0.1Et0.05Heure,Correspondantz0.1/2＝1.645,z0.05/2＝1.96.
（1）Proportion globaleπDe90%L'intervalle de confiance pour：

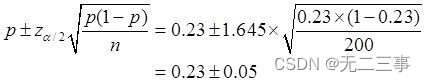
C'est - à - dire:（0.18,0.28）.
（2）Proportion globaleπDe95%L'intervalle de confiance pour：

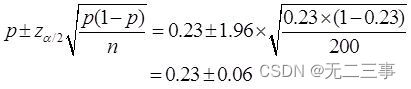
C'est - à - dire:（0.17,0.29）.

7 La direction d'une banque veut estimer le dépôt mensuel moyen par client à la Banque . Il a supposé que l'écart type des dépôts mensuels de tous les clients était 1000Yuan, L'erreur d'estimation requise est 200Moins de yuan.Le niveau de confiance est99%, Quelle taille d'échantillon doit être choisie ？Solution：Connu pour：σ＝1000,Erreur d'estimationE＝200,α＝0.01,z0.01/2＝2.58. La taille de l'échantillon à prélever est donc la suivante: ：

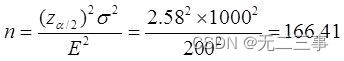
Il faut donc extraire 167Échantillons.

8 Copropriétaires d'un quartier résidentiel 500Ménages, Le Directeur de la communauté est prêt à adopter une nouvelle installation d'approvisionnement en eau , Pour savoir si les résidents sont d'accord . La méthode d'échantillonnage répétée a été utilisée pour l'échantillonnage aléatoire. 50Ménages,Dont:32 Oui. ,18 Objection des ménages .
（1） Intervalle de confiance pour la proportion de ménages favorables à la réforme dans l'ensemble （α＝0.05）.
（2） Si l'Administrateur de la cellule s'attend à ce que le pourcentage d'approbation atteigne 80%, L'erreur d'estimation ne dépasse pas 10%. Nombre de ménages à interroger （α＝0.05）？

Solution：（1）Connu pour：n＝50,p＝32/50＝0.64,α＝0.05,z0.05/2＝1.96. Proportion de ménages favorables à la réforme dans l'ensemble 95%L'intervalle de confiance pour：

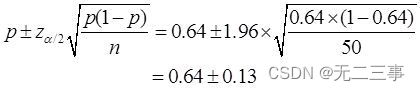
C'est - à - dire:（0.51,0.77）.
（2）Connu pour：π＝0.80,α＝0.05,z0.05/2＝1.96. La taille de l'échantillon à prélever est la suivante: ：

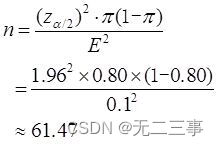
C'est - à - dire que la taille de l'échantillon à prélever est 62Ménages.

9 Selon les résultats de l'échantillon ci - dessous , Calculer l'écart type global σDe90%Intervalle de confiance pour.
（1）x＝21,s＝2,n＝50.
（2）x＝1.3,s＝0.02,n＝15.
（3）x＝167,s＝31,n＝22.

Solution：（1）Connu pour：x＝21,s＝2,n＝50,α＝0.1,Regarde le tableau.：χ20.1/2（50－1）＝66.3387,χ21－0.1/2（50－1）＝33.9303.Variance globaleσ2L'intervalle de confiance pour：

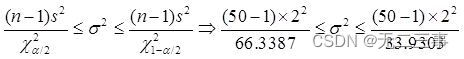
C'est - à - dire:2.95≤σ2≤5.78. L'intervalle de confiance de l'écart type est ：1.72≤σ≤2.40.

（2）Connu pour：x＝1.3,s＝0.02,n＝15,α＝0.1,Regarde le tableau.：χ20.1/2（15－1）＝23.6848,χ21－0.1/2（15－1）＝6.5706.Variance globaleσ2L'intervalle de confiance pour：

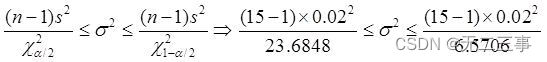
L'intervalle de confiance de l'écart type est ：0.015≤σ≤0.029.
（3）Connu pour：x＝167,s＝31,n＝22,α＝0.1,Regarde le tableau.：χ20.1/2（22－1）＝32.6706,χ21－0.1/2（22－1）＝11.5913.Variance globaleσ2L'intervalle de confiance pour：

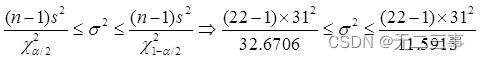
L'intervalle de confiance de l'écart type est ：24.85≤σ≤41.73.

10 Les clients doivent souvent attendre un certain temps pour faire des affaires à la Banque , Le temps d'attente est lié à de nombreux facteurs. .Par exemple,, Vitesse de traitement des affaires par le banquier , Mode d'attente des clients, etc. .À cette fin,, Une banque est prête à tester deux types de files d'attente , La première façon de faire la queue est ： Tous les clients entrent dans une file d'attente ; La deuxième façon de faire la queue est ： Les clients attendent trois rangées dans trois fenêtres d'affaires . Pour comparer les files d'attente qui réduisent le temps d'attente des clients , Sélection aléatoire des banques 10Clients, Le temps qu'ils attendent pour faire des affaires （Unité：Minutes）,Comme indiqué dans le tableau.

Exigences：
（1） Construire la première méthode de mise en file d'attente 95%Intervalle de confiance pour.
（2） Construire la deuxième méthode de mise en file d'attente 95%Intervalle de confiance pour.
（3）Selon（1）Et（2）Les résultats de, Quelle est la meilleure façon de faire la queue? ？

Solution：（1）Connu pour：n＝10,α＝0.05,Regarde le tableau.χ0.05/22（10－1）＝19.0228,χ1－0.05/22（10－1）＝2.7004. Selon les modalités 1 Les données de l'échantillon sont calculées comme suit: ：s2＝0.2272.Variance globaleσ2L'intervalle de confiance pour：

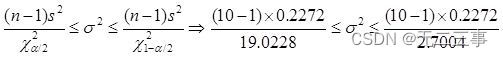
L'intervalle de confiance de l'écart type est ：0.33≤σ≤0.87.
（2） Selon les modalités 2 Les données de l'échantillon sont calculées comme suit: ：s2＝3.3183.Variance globaleσ2L'intervalle de confiance pour：

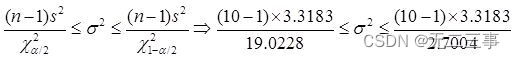
L'intervalle de confiance de l'écart type est ：1.25≤σ≤3.33.
（3） La première façon de faire la queue est meilleure , Parce qu'il est moins discret que la deuxième file d'attente .

11 Deux échantillons aléatoires indépendants ont été prélevés sur deux populations normales. , Leurs moyennes et leurs écarts types sont présentés dans le tableau ci - dessous. .

（1）Mise en placen1＝n2＝100,S'il te plaît.（μ1－μ2）95%Intervalle de confiance pour.
（2）Mise en placen1＝n2＝10,σ12＝σ22,S'il te plaît.（μ1－μ2）95%Intervalle de confiance pour.

（3）Mise en placen1＝n2＝10,σ12≠σ22,S'il te plaît.（μ1－μ2）95%Intervalle de confiance pour.
（4）Mise en placen1＝10,n2＝20,σ12＝σ22,S'il te plaît.（μ1－μ2）95%Intervalle de confiance pour.
（5）Mise en placen1＝10,n2＝20,σ12≠σ22,S'il te plaît.（μ1－μ2）95%Intervalle de confiance pour.

Solution：（1） Parce que les deux échantillons sont de grands échantillons indépendants ,σ12Etσ22Inconnu.Quandα＝0.05Heure,z0.05/2＝1.96,Etμ1－μ2De95%L'intervalle de confiance pour：

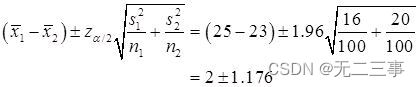
C'est - à - dire:（0.824,3.176）.
（2） Comme les deux échantillons sont de petits échantillons indépendants d'une population normale ,Quandσ12Etσ22Inconnu maisσ12＝σ22Heure, La variance de deux échantillons est nécessaire s12Ets22 Et pour estimer . Estimation combinée de la variance globale sp2Pour：

Quandα＝0.05Heure,t0.05/2（10＋10－2）＝2.101,Etμ1－μ2De95%L'intervalle de confiance pour：

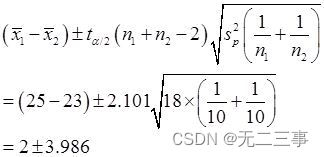
C'est - à - dire:（－1.986,5.986）.
（3） Comme les deux échantillons sont de petits échantillons indépendants d'une population normale ,σ12Etσ22 Inconnu et σ12≠σ22,n1＝n2＝n.Quandα＝0.05Heure,t0.05/2（10＋10－2）＝2.101,Etμ1－μ2De95%L'intervalle de confiance pour：

C'est - à - dire:（－1.986,5.986）.
（4） Comme les deux échantillons sont de petits échantillons indépendants d'une population normale ,σ12Etσ22Inconnu maisσ12＝σ22,n1≠n2. La variance de deux échantillons est nécessaire s12Ets22Pour estimer. Estimation combinée de la variance globale sp2Pour：

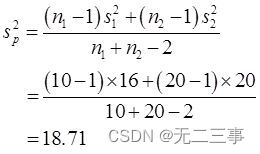
Quandα＝0.05Heure,t0.05/2（10＋20－2）＝2.048.Donc,,μ1－μ2De95%L'intervalle de confiance pour：

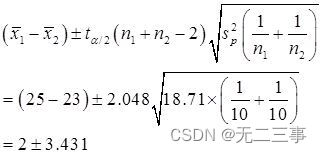
C'est - à - dire:（－1.431,5.431）.

（5） Comme les deux échantillons sont de petits échantillons indépendants d'une population normale ,σ12Etσ22 Inconnu et σ12≠σ22,n1≠n2.Donc,,μ1－μ2De95%L'intervalle de confiance pour：

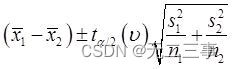
Les degrés de liberté sont calculés comme suit: ：

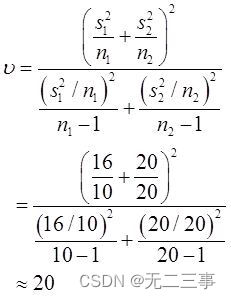
Quandα＝0.05Heure,t0.05/2（20）＝2.086.μ1－μ2De95%L'intervalle de confiance pour：

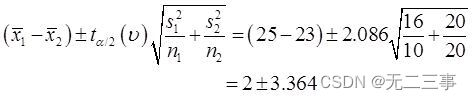
C'est - à - dire:（—1.364,5.364）.

12Tableau7-8C'est par4 Échantillons aléatoires composés d'observations .

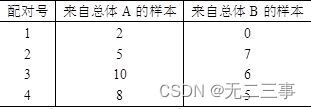
（1）CalculAAvecB Différence entre les observations de chaque paire , Calcul de la différence de réutilisation dEtsd.
（2）Mise en placeμ1Etμ2 Total, respectivement AEt en généralBLa moyenne de,Structureμd＝μ1－μ2De95%Intervalle de confiance pour.

Solution：（1） Le processus de calcul est indiqué dans le tableau ci - dessous. 7-9Comme indiqué.

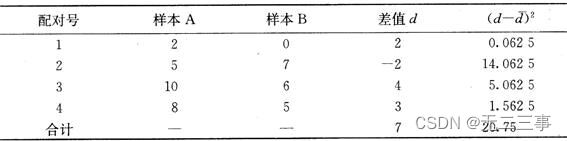
 d＝7/4＝1.75

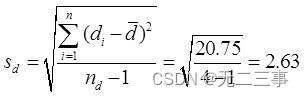
（2）Quandα＝0.05Heure,t0.05/2（4－1）＝3.182. Différence entre deux échantillons μd＝μ1－μ2De95%L'intervalle de confiance pour：

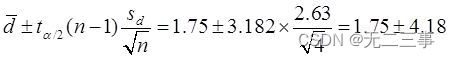
C'est - à - dire:（－2.43,5.93）.

13 Une agence d'évaluation des talents 10 Les gestionnaires de petites entreprises utilisent deux méthodes pour tester leur confiance , Les résultats du test de confiance en soi sont présentés dans le tableau ci - dessous. 7-10Comme indiqué.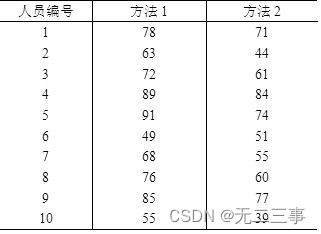

Exigences： Construire la différence moyenne de confiance en soi entre les deux méthodes μd＝μ1－μ2De95%Intervalle de confiance pour.

Solution： Calculé à partir des données de l'échantillon ：d＝[（78－71）＋（63－44）＋…＋（55－39）]/10＝110/10＝11

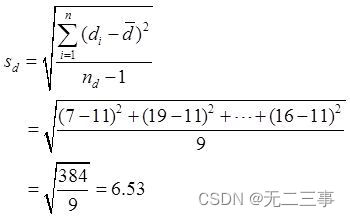
Quandα＝0.05Heure,t0.05/2（10－1）＝2.262. Différence entre les scores moyens de confiance en soi des deux méthodes μd＝μ1－μ2De95%L'intervalle de confiance pour：

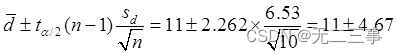
C'est - à - dire:（6.33,15.67）.

14 Une de chacune des deux populations n1＝n2＝250 Échantillons aléatoires indépendants de ,De l'ensemble1 La proportion d'échantillons pour p1＝40%,De l'ensemble2 La proportion d'échantillons pour p2＝30%.Exigences：
（1）Structureπ1－π2De90%Intervalle de confiance pour.

（2）Structureπ1－π2De95%Intervalle de confiance pour.

Solution：（1）Connu pour：n1＝n2＝250,p1＝40%,p2＝30%,α＝0.1,z0.1/2＝1.645.π1－π2De90%L'intervalle de confiance pour：

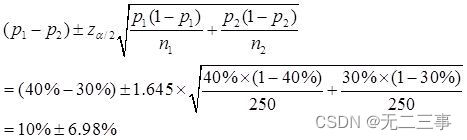
C'est - à - dire:（3.02%,16.98%）.
（2）α＝0.05,z0.05/2＝1.96.π1－π2De90%L'intervalle de confiance pour：

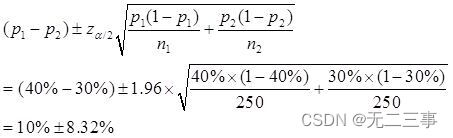
C'est - à - dire:（1.68%,18.32%）.

15 La variance du processus de production est une mesure importante de la qualité du processus .Quand la variance est grande, Le processus doit être amélioré pour réduire la variance .Tableau7-11 Est le poids du sachet de thé produit par deux machines （Unité：g）Données.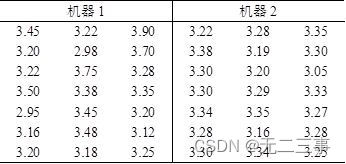

Exigences： Construire deux rapports de variance globale （σ12/σ22）95%Intervalle de confiance pour.Solution： Calculé à partir des données de l'échantillon ：s12＝0.058375,s22＝0.005846.Quandα＝0.05Heure,ParExce1De“FINV” Fonction calculée ：F0.025（21－1,21－1）＝2.46,F1－α/2（n1－1,n2－1）＝F0.975（21－1,21－1）＝0.41.Deux rapports de variance globaleσ12/σ22De95%L'intervalle de confiance pour：

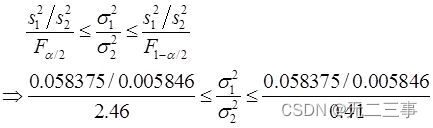
C'est - à - dire deux rapports de variance globale σ12/σ22De95%L'intervalle de confiance pour：4.06≤σ12/σ22≤24.35.

16 Sur la base des données de production antérieures , Le taux de rejet d'un produit est 2%. Si l'intervalle de confiance est 95%, L'erreur d'estimation ne dépasse pas 4%, Combien d'échantillons doivent être prélevés ？Solution：Connu pour：π＝2%,E＝4%,Quandα＝0.05Heure,z0.05/2＝1.96. La taille de l'échantillon à prélever est la suivante: ：

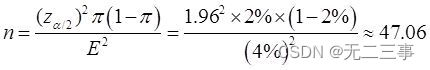
Par conséquent, la taille minimale de l'échantillon doit être: 48Échantillons.