当前位置:网站首页>Quaternion -- basic concepts (Reprint)
Quaternion -- basic concepts (Reprint)
2022-07-06 14:36:00 【Lntan0】
from :https://zhuanlan.zhihu.com/p/27471300
1. Why use quaternions
Maybe everyone has seen the origin of quaternion many times . Long ago , An old man is sitting by the bridge , Look at the passing ships , All of a sudden a flash of inspiration , Engrave a few lines of big characters on the stone tablet beside the bridge , Quaternion was born ! Everyone loves to hear stories , So why do we need quaternions ? One way is to solve vector multiplication , We know that multiplication between vectors has inner product and outer product , But neither of these two operations is perfect , That is, the condition of the group is not satisfied ( Of course, when quaternion was born, there was no saying of inner product and outer product ). Is there such a perfect multiplication between vectors , So the problems that cannot be solved in three-dimensional space are mapped to four-dimensional space . This is the opportunity for the birth of quaternions .
So here comes the question , Since quaternion is only for matrix multiplication , So why do we now use quaternions to rotate , Even replaced Euler angle 、 Shaft angle and other forms ? First , Quaternions are not born to solve three-dimensional rotation , But its nature is very conducive to the expression of rotation information ( We'll talk more about that later ), Therefore, to understand the properties of quaternions is prior to the application of quaternions in rotation . As for Quaternion replacing Euler angle and other forms , It needs to involve some other knowledge points , Let me first list the advantages of quaternion over other forms :
Solve the universal joint deadlock (Gimbal Lock) problem
Just store 4 A floating point number , Lighter than matrix
Quaternion, whether it's inverse 、 Series operation, etc , More efficient than matrix
So take it into consideration , Now mainstream games or animation engines will scale vectors + Rotating quaternion + The motion data of the character is stored in the form of translation vector .
2. How did you come up with quaternion
Mediocre tutorials will directly propose the definition of quaternion 、 Operation rules and so on , Then the reader is at a loss . contrary , More systematic tutorials generally start with the plural (Complex Number) To guide , Gradually put forward the definition of quaternion , This will make it easier for readers to understand , It is also better to form a picture in the brain . The relationship between complex numbers and quaternions 、 And how to extend the concept of complex number to quaternion is an idea we need to clarify .
Let's start with a few concepts .
Subspace in space : generally speaking , Space ( dimension >2) There are lower dimensional subspaces , For example, one-dimensional subspace in two-dimensional space , It's a straight line ; One dimensional subspace and two-dimensional subspace in three-dimensional space , That is, lines and faces . When we go beyond the concept of three-dimensional, it is difficult to imagine what it looks like , But there must be three-dimensional subspace or two-dimensional subspace in four-dimensional space . We'll add a prefix here (hyper) To describe these spaces , For example, a plane in a high-dimensional space is called a hyperplane .
Mapping between space and subspace : We express two-dimensional space as (x,y), When y=0 when , In fact, it can be regarded as one-dimensional , It just means (x,0) This form . Push to the fourth dimension ,(w,x,y,z), When w=0 when ,(0,x,y,z) It's a three-dimensional subspace , That's why we can manipulate three-dimensional vectors with unit quaternions , In fact, we are mapping a three-dimensional vector to a four-dimensional three-dimensional subspace (w=0, This form also becomes a pure quaternion ), Then rotate it , The final vector result is still in this three-dimensional subspace , So it can be mapped back to three-dimensional space .
Guangyiqiu : The ball here is generalized . We're on a two-dimensional plane , The generalized ball actually refers to circle, Three dimensional space is our cognitive ball , be called two-sphere, The generalized sphere in four-dimensional space is actually a hypersphere (hyper-sphere), Also known as three-sphere. The unit vector is actually the point on the generalized Ball , And the unit quaternion is three-sphere The point above .
Constraints and eigenvectors : A point in space is represented by x, y, z And other parameters , In general, the number of parameters is equal to the dimension , Points in two-dimensional space {x, y} Parameters , Points in four-dimensional space {x, y, z, w} Parameters . But to constrain the points in space , This will reduce the number of parameters , For example, a point in three-dimensional space is on a unit sphere , The original three parameters {x, y, z} The point that can be expressed now only needs two parameters {u, v} It can express . If {u, v} It's the unit vector , It can also be called {u, v} yes {x, y, z} Eigenvector of .
The above concept gives you an idea , Quaternion is not a thing that can be achieved overnight , In terms of space , It is essentially no different from the well-known low dimensional space , Or it has a lot in common . Many properties of quaternions are extended from low dimensions , More specifically, it is extended from the concept of plural .
Then what is plural ?
The concept of plural number is very simple , It is actually to meet the obsessive-compulsive disorder of mathematicians ,-1 The square root of must be meaningful . Seemingly meaningless plural , But it is very useful in practice . Let's first look at its geometric expression , Make x It is the real part ,y It is the imaginary part , be x+iy It can be represented as the following figure .
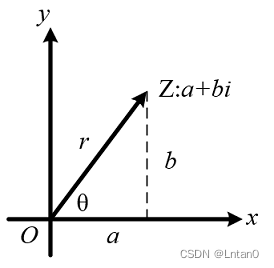
The proposition of complex number directly adds a dimension to the original one-dimensional numerical range , The increase of data volume can be said to be huge . Let's think about complex numbers from the perspective of polar coordinates ,x+i·y It can be written. r·cosθ+i·r·sinθ, We only consider the unit plural ,|r|=1, And you get cosθ+i·sinθ. Speaking of this , It is necessary to propose a formula commonly used in algebra —— Euler formula , Basically, this formula will be used in all operations of complex numbers .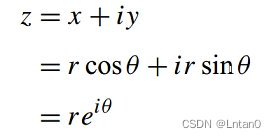
Next, I won't talk about the multiplication of complex numbers , Unit complex multiplication can achieve a two-dimensional rotation effect , If you are interested, you can draw a picture here , Push... Push . Let me first introduce how to derive quaternions from complex numbers , Just as a complex number is composed of a real part and an imaginary part , Then we will replace one imaginary part with three imaginary parts , That is, two intersect {i, j, k}.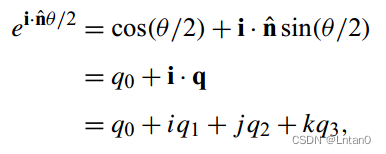
among n Is a three-dimensional unit vector ,i²=j²=k²=i·j·k=-1. This is the conventional expression of quaternion , But unit quaternions have a lot of constraints , Not all four-dimensional vectors are quaternions .
Here is another brain hole , Maybe you heard about quaternion 、 Octet , But there are ternary numbers 、 Pentagram ? In fact, objectively speaking , Ternary number 、 Four yuan number 、n All elements exist ( That is, there are infinite levels of complex numbers ), But not all number systems satisfy modular operation . And with the improvement of dimension , Features will gradually be sacrificed , Compared with complex number operation , Quaternions sacrifice the commutative law ; Compared with quaternion operation , Octuples sacrifice the law of Association . Of course, there are also sixteen elements , But hexadecimals will have fewer features , It is even more meaningless in Mathematics , So quaternions are the most widely used .
3. How to understand quaternion
Now let's summarize the quaternion properties that have been obtained .
Four yuan number ( It doesn't refer specifically to Four yuan number = The unit is 4 yuan ) Is the point above a hypersphere in four-dimensional space , Satisfy w²+x²+y²+z²=1; A pure quaternion is a four-dimensional space in w=0 Point of a subspace of time , In the form of {0, q}, In particular, pure quaternion and quaternion are different concepts .
Quaternions are the result of the extension of the imaginary part of complex numbers , The imaginary part of a complex number is 1 individual , And the imaginary part of a quaternion has 3 individual , And they are orthogonal to each other , The real part is cosθ/2, The imaginary part is a potential axis multiplied by sinθ/2.
Quaternion degrees of freedom have no four dimensions , Due to the existence w²+x²+y²+z²=1 This constraint , Its degree of freedom is actually only 3, And each quaternion can correspond to an eigenvector , namely n. But remember that quaternions do not correspond to eigenvectors one by one , It will be said later .
Because quaternions exist in four-dimensional space , Therefore, how to use low dimensional information to understand high-dimensional information is particularly important . Let's take three-dimensional as an example , The three-dimensional sphere is expressed algebraically as x²+y²+z²=1, Although the point on the ball is made by x,y,z Three parameters to determine , But actually we only need two . Suppose to take x and z Express , among y Can pass x and z To solve the . that , We will y Axis information is hidden , Just look at the projection plane , As shown in the figure below . This picture means , The whole ball is XOZ The projection on the plane is a circle , When a point of the sphere is projected on a circle ,y=0; When the position of the projection is in the circle , There are two cases ,y>0 In the northern hemisphere ,y<0 In the southern hemisphere . So we can restore the whole sphere only through the projected circle .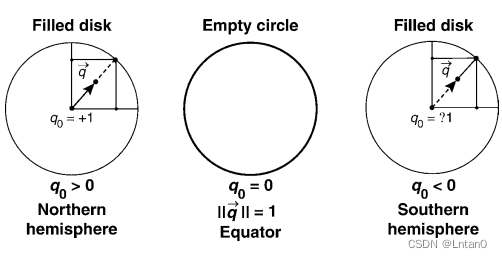
Let's extend it to four dimensions ,w²+x²+y²+z²=1 To take x、y and z To represent the superball . As shown in the figure below , Project a four-dimensional space onto a three-dimensional hyperplane (w=0) It could be a two-sphere. When the projection point is in the whole two-sphere At the edge of ,w It must be 0, It is worth mentioning that the quaternion in this space is a pure quaternion . When the projection point falls on two-sphere When inside , There are also two situations ,w>0 and w<0. But we can find that the corresponding eigenvectors in these two cases are the same , So when we convert a rotation matrix to a quaternion , There are two corresponding values , The range of quaternions is 2 Times over 3D rotate (2:1 mapping).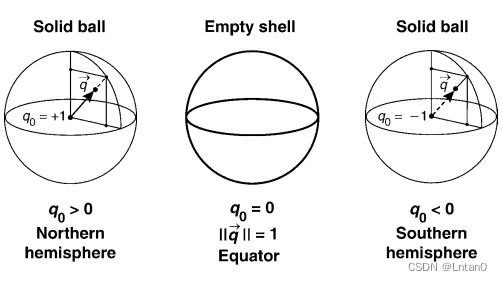
The above two paragraphs are relatively mysterious , But I think it is quite helpful to understand four-dimensional space and quaternion . This article has limited expressive ability , If you really don't understand , You can flip through 《Visualizing Quaternions》 Chapter viii. , Personally, I think this is one of the most wonderful parts of the book .
4. Quaternion “ Multiplication ” operation
The quaternion is mentioned above “ Multiplication ” The rule is to satisfy the property of the Group , What kind of multiplication is that , How to satisfy , Now let's take a look .
Because quaternions have i,j,k Three imaginary parts , So I have to be satisfied i²=j²=k²=i·j·k=-1 This condition . Here is the order * by “ Multiplication ” The operator , be p*q The formula is as follows , I won't write the specific derivation steps .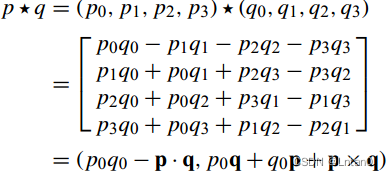
Let's start with the unit quaternion , Pass one by one according to the nature of the Group :
Sealing property : Easy to prove ,p and p Conjugate multiplication of ,|p*q|=1.
Associative law : This is also a good proof , Just prove (p*q)*r=p*(q*r).
The above two proofs are not detailed here , After all, it's not easy to edit formulas . We can change our thinking , Think geometrically , Because the unit quaternion is still the unit quaternion after rotation , So it satisfies the closeness . meanwhile , Analogy matrix multiplication , The unit quaternion should also satisfy the law of Association .
Unit element :e=(1,0,0,0), This is also an initial value of quaternion ( Equivalent to the identity matrix ). It can be seen from the above formula ,p*(1,0,0,0) Or is it equal to p.
Inverse element :p There is a quaternion ,* The result of the operation is e, Refer to the following formula for details , It can be seen that the inverse element is its conjugate divided by the square of the module .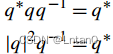
If this is plural , It may also satisfy the commutative law , It is an Abelian group . But quaternions certainly do not satisfy the commutative law , From an algebraic point of view , Or from a geometric point of view . Come here , Basically, I have introduced the multiplication of quaternions , If you use its exponential form (exp form ), It will be simpler to prove these properties .
5. The exponent of quaternion 、 Logarithm and inner product
According to Euler formula , The exponential form of quaternion is just another expression , All express the same thing . And its logarithmic form is the exponent of quaternion exponential form , As shown in the formula below . This formula is very useful when calculating quaternion interpolation , This will be discussed later .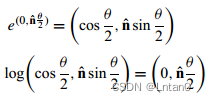
So what is the relationship between logarithm and exponent ? Let's refer to the figure below , In fact, the change of logarithm is actually the size of angle , So the relationship between exponential form and logarithmic form of quaternion can be seen intuitively with the figure below .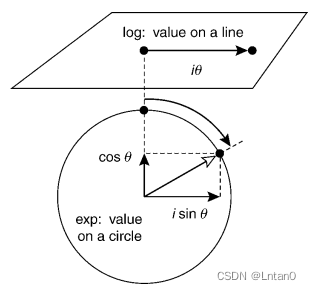
Finally, let's introduce the inner product of quaternions . Let's first look at three-dimensional space or two-dimensional space , If two unit vectors are inner products , The result of inner product is the angle between two vectors . The same is true of quaternions , The inner product of the quaternion of two units is its included angle , This conclusion is extended to n Wei is also established , The reason is simple , Because three points are coplanar , Even if n Dimensional space , The space of two vectors is only a two-dimensional subspace . As for the outer product , Because for complex numbers and quaternions , The meaning of outer product is not very obvious , There will be no too much discussion here .
边栏推荐
- 攻防世界MISC练习区(SimpleRAR、base64stego、功夫再高也怕菜刀)
- 【指针】删除字符串s中的所有空格
- 数据库多表链接的查询方式
- Intranet information collection of Intranet penetration (3)
- {1,2,3,2,5}查重问题
- JDBC read this article is enough
- Uibutton status exploration and customization
- Bing Dwen Dwen official NFT blind box will be sold for about 626 yuan each; JD home programmer was sentenced for deleting the library and running away; Laravel 9 officially released | Sifu weekly
- Attack and defense world misc practice area (GIF lift table ext3)
- Pointers: maximum, minimum, and average
猜你喜欢

Apache APIs IX has the risk of rewriting the x-real-ip header (cve-2022-24112)
Library management system
Statistics 8th Edition Jia Junping Chapter IX summary of knowledge points of classified data analysis and answers to exercises after class

Constants, variables, and operators of SystemVerilog usage
![[paper reproduction] cyclegan (based on pytorch framework) {unfinished}](/img/16/43d8929d1a37c1c68e959d5854e18c.jpg)
[paper reproduction] cyclegan (based on pytorch framework) {unfinished}
《统计学》第八版贾俊平第三章课后习题及答案总结

Fundamentals of digital circuit (V) arithmetic operation circuit
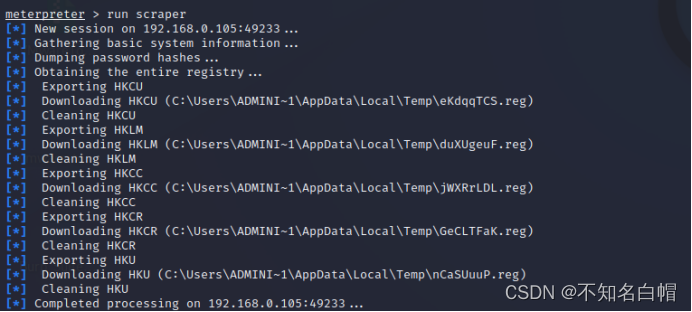
内网渗透之内网信息收集(四)
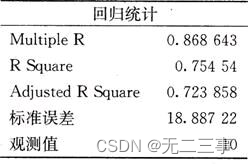
《统计学》第八版贾俊平第十一章一元线性回归知识点总结及课后习题答案
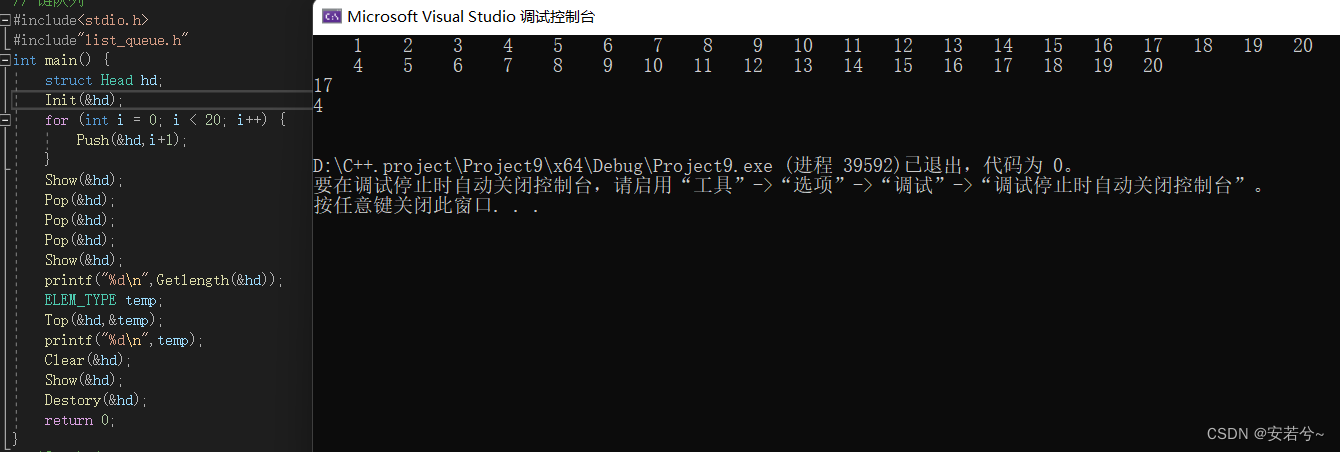
链队实现(C语言)
随机推荐
函数:用牛顿迭代法求方程的根
Get started with Matplotlib drawing
Sqqyw (indifferent dot icon system) vulnerability recurrence and 74cms vulnerability recurrence
函数:求1-1/2+1/3-1/4+1/5-1/6+1/7-…+1/n
内网渗透之内网信息收集(二)
刷视频的功夫,不如看看这些面试题你掌握了没有,慢慢积累月入过万不是梦。
Web vulnerability - File Inclusion Vulnerability of file operation
Lintcode logo queries the two nearest saplings
On the idea of vulnerability discovery
Captcha killer verification code identification plug-in
安全面试之XSS(跨站脚本攻击)
《统计学》第八版贾俊平第六章统计量及抽样分布知识点总结及课后习题答案
循环队列(C语言)
数字电路基础(五)算术运算电路
[pointer] use the insertion sorting method to arrange n numbers from small to large
SQL injection
Statistics, 8th Edition, Jia Junping, Chapter 6 Summary of knowledge points of statistics and sampling distribution and answers to exercises after class
移植蜂鸟E203内核至达芬奇pro35T【集创芯来RISC-V杯】(一)
指针--剔除字符串中的所有数字
. Net6: develop modern 3D industrial software based on WPF (2)