当前位置:网站首页>数字电路基础(二)逻辑代数
数字电路基础(二)逻辑代数
2022-07-06 09:24:00 【ブリンク】
数字电路基础(二)逻辑代数
一、逻辑变量和逻辑函数
熟悉计算机编程语言的同学应该了解,在很多编程中存在一种布尔变量,它有且只有两个值真和假(True和False,有时也使用1和0)。布尔变量本身实际上可以算是一种逻辑变量,符合逻辑变量的特点。在给定确定的输入时,通常输出可以被唯一地确定。
我们假设有两个输入 A A A和 B B B,有一个输出 F F F,它们之间的逻辑表达式满足 F = f ( A , B ) F=f(A,B) F=f(A,B),其中 A , B , F A,B,F A,B,F被称为逻辑变量,变量 A A A和 B B B称为逻辑自变量, F F F被称为逻辑因变量(也称作逻辑函数)。逻辑变量通常只取0或1两个值,他可以在电路中来表示,电平的高与低,开关的断开与连接等状态。
在逻辑电路中,高低电平的定义并不只是唯一的值来确定,它们都是一定的定压范围。例如:在TTL电路中,高电平通常为2-5V,低电平通常为0-0.8V
二、基本逻辑运算和基本逻辑门
在逻辑电路中有三种基本的逻辑运算:逻辑与,逻辑或,逻辑非。而用来实现这三种逻辑运算的电路分别为与门,或门,非门。下面分别介绍这三种逻辑运算及门电路。
1.逻辑与
逻辑与是指在决定一个事件的全部条件都成立时,这个事件才会发生。如下图所示电路展示了用开关控制的电路如何实现与运算: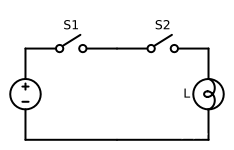
只有当S1和S2两个开关同时闭合时,灯泡L才会亮;若其中有任意一个开关断开,则灯泡L不会亮。
将 A A A, B B B, F F F的所有状态列在一个表中,此表称为真值表,如下表所示:
从真值表可以看出与运算和算术中的乘法相似,故逻辑与也叫做逻辑乘
F = A ⋅ B = A B F=A \cdot B=AB F=A⋅B=AB
逻辑与有如下几种运算:
0 ⋅ 0 = 0 , 0 ⋅ 1 = 0 , 1 ⋅ 0 = 0 , 1 ⋅ 1 = 1 0\cdot 0=0,0\cdot 1=0,1\cdot0=0,1\cdot1=1 0⋅0=0,0⋅1=0,1⋅0=0,1⋅1=1
逻辑与的符号如下图所示
2.逻辑或
逻辑与是指在决定一个事件的全部条件中,只要有任意一个条件满足,事件就会发生。如下图所示的电路中展示了用开关控制的电路如何实现或运算:
当S1和S2中任何一个开关闭合时,灯L都会亮;若两个开关全部断开,则灯L不会亮。
或门的真值表如下图所示:
从真值表可以看出或运算和算术中的加法相似,故逻辑或也叫做逻辑加
F = A + B F=A + B F=A+B
逻辑与有如下几种运算:
0 + 0 = 0 , 0 + 1 = 1 , 1 + 0 = 1 , 1 + 1 = 1 0 + 0=0,0 + 1=1,1+0=1,1+1=1 0+0=0,0+1=1,1+0=1,1+1=1
逻辑与的符号如下图所示:
3.逻辑非
逻辑非是指在条件满足的情况下,事件不发生;条件不满足的情况下,事件发生。如下如所示的电路中展示了用开关控制电路如何实现非运算:
当开关S断开时,电源、电阻R和灯泡L形成通路,灯泡点亮;当开关S闭合时,灯泡L被开关S短路,灯泡不亮。
非门的真值表如下图所示:
其表达式为:
F = A ‾ F=\overline{A} F=A
非运算规则为:
0 ‾ = 1 , 1 ‾ = 0 \overline{0}=1,\overline{1}=0 0=1,1=0
4.复合逻辑运算
(1)与非运算
逻辑表达式为: F = A B ‾ F=\overline{AB} F=AB,它是由逻辑变量先做与运算,再做非运算得到的,逻辑符号如下图所示:
(2) 或非运算
逻辑表达式为: F = A + B ‾ F=\overline{A+B} F=A+B,它是由逻辑变量先做或运算,再做非运算得到的,逻辑符号如下图所示:
(3) 与或非运算
逻辑表达式为: F = A B + C D ‾ F=\overline{AB+CD} F=AB+CD,它是由逻辑变量先做与运算,再做或运算,最后做非运算得到的,逻辑符号如下图所示: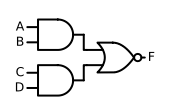
(4)异或运算
逻辑表达式为: F = A B ‾ + A ‾ B = A ⊕ B F=A\overline{B}+\overline{A}B=A\oplus B F=AB+AB=A⊕B. 异或运算规则是:当输入的两个逻辑变量相同时,则输出为0;当输入的两个逻辑变量不同时,则输出为1。逻辑符号如下图所示:
(5)同或运算
逻辑表达式为: F = A B + A B ‾ = A ⊙ B F=AB+\overline{AB}=A\odot B F=AB+AB=A⊙B. 同或运算规则是:当输入的两个逻辑变量相同时,则输出为1;当输入的两个逻辑变量不同时,则输出为0。逻辑符号如下图所示:
三、逻辑代数基本公式和常用公式
1.基本公式
(1)0-1律 A ⋅ 0 = 0 A\cdot 0=0 A⋅0=0 A + 1 = 1 A+1=1 A+1=1
(2)自等律 A ⋅ 1 = A A\cdot 1=A A⋅1=A A + 0 = A A+0=A A+0=A
(3)重叠律 A ⋅ A = A A\cdot A=A A⋅A=A A + A = A A+A=A A+A=A
(4)互补律 A ⋅ A ‾ = 0 A\cdot \overline{A}=0 A⋅A=0 A + A ‾ = 1 A+ \overline{A}=1 A+A=1
(5)交换律 A ⋅ B = B ⋅ A A\cdot B=B\cdot A A⋅B=B⋅A A + B = B + A A+B=B+A A+B=B+A
(6)结合律 A ⋅ ( B ⋅ C ) = ( A ⋅ B ) ⋅ C A\cdot(B\cdot C)=(A\cdot B)\cdot C A⋅(B⋅C)=(A⋅B)⋅C
A + ( B + C ) = ( A + B ) + C A+(B+C)=(A+B)+C A+(B+C)=(A+B)+C
(7)分配率 A ⋅ ( B + C ) = A B + A C A\cdot(B+C)=AB+AC A⋅(B+C)=AB+AC
A + ( B + C ) = ( A + B ) ( A + C ) A+(B+C)=(A+B)(A+C) A+(B+C)=(A+B)(A+C)
(8)吸收率 A ⋅ ( A + B ) = A A\cdot(A+B)=A A⋅(A+B)=A A + A B = A A+AB=A A+AB=A
(9)反演律 A B ‾ = A ‾ + B ‾ \overline{AB}=\overline{A}+\overline{B} AB=A+B A + B ‾ = A ‾ ⋅ B ‾ \overline{A+B}=\overline{A}\cdot \overline{B} A+B=A⋅B
(10)双重否定率 A ‾ ‾ = A \overline{\overline{A}} = A A=A
反演律是其中使用较多的,在化简逻辑表达式时有重要作用
2.基本规则
(1)代入规则
在任何一个逻辑等式中,如果将等式两边所有出现过的变量都使用一个逻辑函数替代,则此等式仍然成立。
例如: A ⋅ B ‾ = A ‾ + B ‾ \overline{A\cdot B}=\overline{A}+\overline{B} A⋅B=A+B中的 A A A使用 F = A C F=AC F=AC替代,则原式变为: A C ⋅ B ‾ = A C ‾ + B ‾ = A ‾ + B ‾ + C ‾ \overline{AC\cdot B}=\overline{AC}+\overline{B}=\overline{A}+\overline{B}+\overline{C} AC⋅B=AC+B=A+B+C.依然成立。
(2)反演规则
当我们需要求解一个逻辑函数 F F F的反函数 F ‾ \overline{F} F时,可以使用反演规则。
只需要将 F F F中的
⋅ 变 为 + , + 变 为 ⋅ , 1 变 为 0 , 0 变 为 1 , 变 量 取 反 \cdot变为+, +变为\cdot ,1变为0 ,0变为1,变量取反 ⋅变为+,+变为⋅,1变为0,0变为1,变量取反
即可.
需要注意的是:变更反变量时,有两个变量以上公用的取反号不变
例如:求 F = A + B + C ‾ + D + E ‾ ‾ ‾ + ( G ⋅ H ) F=A+\overline{B+ \overline{C} +\overline{D+\overline{ E}}}+(G\cdot H) F=A+B+C+D+E+(G⋅H)的反函数
F ‾ = A ‾ ⋅ B ‾ ⋅ C ⋅ D ‾ ⋅ E ‾ ‾ ⋅ ( G ‾ + H ‾ ) \overline{F}=\overline{A}\cdot \overline{\overline{B}\cdot C \cdot \overline{\overline{D}\cdot E}}\cdot (\overline{G}+\overline{H}) F=A⋅B⋅C⋅D⋅E⋅(G+H)
(3)对偶规则
当我们需要求解一个逻辑函数 F F F的对偶式 F ′ F' F′时,
只需要将 F F F中的
⋅ 变 为 + , + 变 为 ⋅ , 1 变 为 0 , 0 变 为 1 \cdot变为+, +变为\cdot ,1变为0 ,0变为1 ⋅变为+,+变为⋅,1变为0,0变为1
即可.
两个逻辑函数相等 ⇔ \Leftrightarrow ⇔两个逻辑函数的对偶式相等(充分必要条件)
例如:求 F = A ⋅ B + A ‾ ⋅ C + B ⋅ C F=A\cdot B+\overline{A}\cdot C+B\cdot C F=A⋅B+A⋅C+B⋅C的对偶式
F ′ = ( A + B ) ⋅ ( A ‾ + C ) ⋅ ( B + C ) F'=(A+B)\cdot (\overline{A}+C) \cdot (B+C) F′=(A+B)⋅(A+C)⋅(B+C)
3.常用公式
公式1 A B + A B ‾ = A AB+A\overline{B}=A AB+AB=A
证明: A B + A B ‾ = A ( B + B ‾ ) = A AB+A\overline{B}=A(B+\overline{B})=A AB+AB=A(B+B)=A
公式2 A + A B ‾ = A + B A+A\overline{B}=A+B A+AB=A+B
证明: A + A ‾ B = ( A + A ‾ ) ⋅ ( A + B ) = A + B A+\overline{A}B=(A+\overline{A})\cdot (A+B)=A+B A+AB=(A+A)⋅(A+B)=A+B
公式3 A B + A ‾ C + B C = A B + A ‾ C AB+\overline{A}C+BC=AB+\overline{A}C AB+AC+BC=AB+AC
证明: A B + A ‾ C + B C = A B + A ‾ C + B C ( A + A ‾ ) = A B + A ‾ C + A B C + A ‾ B C = A B + A ‾ C AB+\overline{A}C+BC=AB+\overline{A}C+BC(A+\overline{A})=AB+\overline{A}C+ABC+\overline{A}BC=AB+\overline{A}C AB+AC+BC=AB+AC+BC(A+A)=AB+AC+ABC+ABC=AB+AC
公式4 A B + A ‾ C ‾ = A B ‾ + A ‾ C ‾ \overline{AB+\overline{A}C}=A\overline{B}+\overline{A}\overline{C} AB+AC=AB+AC
证明: 略
公式5 A ⊕ B ‾ = A ⊙ B \overline{A\oplus B}=A\odot B A⊕B=A⊙B
证明: 略
四、简单介绍几种使用公式法化简的思路
此处的方法名字都是作者本人自己起的,或许更加符合公式意义
(1)去异型
A + A B A+AB A+AB型,此处 A , B A,B A,B可以是一个逻辑表达式而非单独的逻辑变量。直接排出式中的“异类”: B B B,剩余的部分作为结果即 A + A B = A A+AB=A A+AB=A
(2)去非型
A + A ‾ B A+\overline{A}B A+AB型,此处 A , B A,B A,B可以是一个逻辑表达式而非单独的逻辑变量。直接排出式中的“非项”: A ‾ \overline{A} A,剩余的部分作为结果即 A + A ‾ B = A + B A+\overline{A}B=A+B A+AB=A+B
(3)去反型
A B + A ‾ B AB+\overline{A}B AB+AB型,此处 A , B A,B A,B可以是一个逻辑表达式而非单独的逻辑变量。直接排出式中的“相反项”: A ‾ \overline{A} A和 A A A,剩余的部分作为结果即 A B + A ‾ B = B AB+\overline{A}B=B AB+AB=B
(4)三缺一型
一般用于有三个变量,但在逻辑表达式中每一项只有两个逻辑变量的与或式中,可以在缺少某一逻辑变量的后面与运算 ( X + X ‾ ) (X+\overline{X}) (X+X), X X X表示缺少的那个逻辑变量。
举个简单的例子: F = A B ‾ + B C ‾ F=A\overline{B}+B\overline{C} F=AB+BC只需要在 A B ‾ A\overline{B} AB后与运算一个 ( C + C ‾ ) (C+\overline{C}) (C+C), B C ‾ B\overline{C} BC后与运算一个 ( A + A ‾ ) (A+\overline{A}) (A+A)即可。
五、使用卡诺图对逻辑表达式进行化简
1.最小项
想要使用卡诺图进行化简,首先我们需要明白最小项的概念。
在卡诺图中,每一个方格都代表一个最小项。在有 n n n个逻辑变量的逻辑函数中,所有变量的乘积项称为最小项。为什么它被称为最小项,是因为每一个变量在其中都只出现了一次,且都是以它本身或者反变量的形式出现的。类比于做排列组合,将每一个变量只可能出现一次的所有可能全部列出,就是它的全部最小项。
例如:两个变量 A , B A,B A,B的最小项有 2 2 = 4 2^2=4 22=4个( A B , A B ‾ , A ‾ B , A B ‾ AB,A\overline{B},\overline{A}B,\overline{AB} AB,AB,AB,AB)
为了方便,使用 m i m_i mi的形式记录最小项。它的记法是:当逻辑变量在最小项中以原变量出现时,记为1;以反变量出现时,记为0.再将其转化为十进制数,这个十进制数是多少,那么 m i m_i mi的下标 i i i就为多少。
例如: A ‾ B C \overline{A}BC ABC记为二进制数为011,而011对应的十进制数为3,故 A ‾ B C \overline{A}BC ABC记为 m 3 m_3 m3
当我们熟悉了最小项的概念之后,我们可以将任何一个逻辑函数转化为最小项的形式,并使用 m i m_i mi的形式表示.
例如: A B C + A B C ‾ + A ‾ B C + A B ‾ C = m 7 + m 6 + m 3 + m 1 ABC+AB\overline{C}+\overline{A}BC+\overline{AB}C=m_7+m_6+m_3+m_1 ABC+ABC+ABC+ABC=m7+m6+m3+m1
2.卡诺图
(1)两变量卡诺图
下图是两变量的卡诺图:
该图表明, A A A和 B B B都有两种取值0和1,它们可以组成四种组合,每一种组合都是一个最小项。如果用最小项来表示卡诺图则如下图所示:
可以看到其二进制的值对应最小项 m i m_i mi中的 i i i
(2)三变量卡诺图
下面是三变量的卡诺图:
该图表明, A A A, B B B和 C C C都有两种取值0和1,它们可以组成八种组合,每一种组合都是一个最小项。如果用最小项来表示卡诺图则如下图所示:
同样也可以看到其二进制的值对应最小项 m i m_i mi中的 i i i
(4)四变量卡诺图
给出四变量卡诺图的最小项形式:
其确定的方式与二变量和三变量最小项确定的方式是一致的。
三变量和四变量卡诺图00,01,11,10的排列保证了两两之间的不同数只有一个,满足了相邻的条件
3.卡诺图表示逻辑函数
在我们已知逻辑函数的情况下,可以先将逻辑函数化简为最小项表达式,再把对应最小项的卡诺图中的值填为1,其余的填为0即可,也可以直接根据表达式填写卡诺图;若我们直接知道的就是最小项表达式,则可以直接把卡诺图中的对应位置填1,其余填0。
例如:
F = A B C + A B C ‾ + A ‾ B C + A B ‾ C = m 7 + m 6 + m 3 + m 1 F=ABC+AB\overline{C}+\overline{A}BC+\overline{AB}C=m_7+m_6+m_3+m_1 F=ABC+ABC+ABC+ABC=m7+m6+m3+m1
我们已知了它的最小项表达形式,则可以直接在空白卡诺图中填入数字,如下图所示:
4.化简方法
(1)合并最小项
我们可以把卡诺图中相邻的8个、4个、2个、1个的最小项圈起来,进行合并。如下图所示: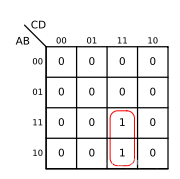
图中的红色圆圈表示把这两项进行合并,很容易看出它们是相邻的。只得注意的是,卡诺图的边界并不是实际意义上的边界。
例如: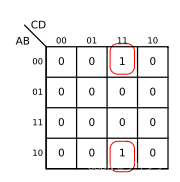
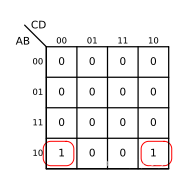
这两种以及其他类似情况都属于两变量合并时的相邻情况
而对于四变量的情况来说,以下两种系列是显而易见的相邻情况: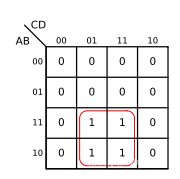
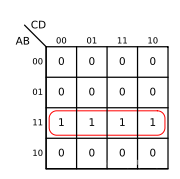
除此之外,还有以下几种情况也属于四个变量相邻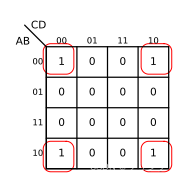

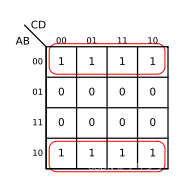
对于八变量的合并情况有如下几种(包括类似的情况):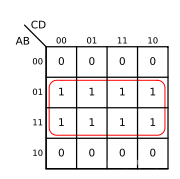
举例:用卡诺图化简 F = A B C D ‾ + A B C ‾ D + A ‾ B C ‾ + A B D ‾ + A ‾ B C + B C D F=\overline{ABCD}+A\overline{BC}D+\overline{A}B\overline{C}+AB\overline{D}+\overline{A}BC+BCD F=ABCD+ABCD+ABC+ABD+ABC+BCD
把逻辑表达式画在卡诺图中,并按照我们刚才讲解的方式进行合并: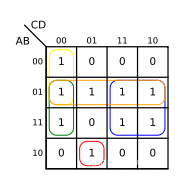
此时,我们只需要把卡诺图上圈起来的部分写成逻辑表达式的形式,再对它们取或操作即可
F = A B C ‾ D + A C D ‾ + A ‾ B + B C + B D ‾ F=A\overline{BC}D+\overline{ACD}+\overline{A}B+BC+B\overline{D} F=ABCD+ACD+AB+BC+BD
(2)含有无关项的卡诺图化简
在一些逻辑函数中,变量取值的某些组合所对应的最小项不会出现或不允许出现,这些最小项称为约束项。一般在卡诺图中用" × \times ×"表示。在这种情况下化简时,可以借助无关项进行最小项的合并。
举例:
F ( A , B , C , D ) = ∑ ( m 15 , m 13 , m 10 , m 6 , m 4 ) + ∑ d ( m 8 , m 7 , m 5 , m 2 , m 1 , m 0 ) F(A,B,C,D)=\sum(m_{15},m_{13},m_{10},m_6,m_4)+\sum_d(m_8,m_7,m_5,m_2,m_1,m_0) F(A,B,C,D)=∑(m15,m13,m10,m6,m4)+∑d(m8,m7,m5,m2,m1,m0)
可以把无关项当做1来处理进行合并。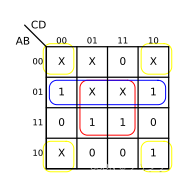
然后还是把圈起来的写成逻辑表达式即可。
F = A ‾ B + B D + B D ‾ F=\overline{A}B+BD+\overline{BD} F=AB+BD+BD
初稿2022/5/5
边栏推荐
- 函数:字符串反序存放
- Data mining - a discussion on sample imbalance in classification problems
- JDBC read this article is enough
- DVWA (5th week)
- Based on authorized access, cross host, and permission allocation under sqlserver
- 《统计学》第八版贾俊平第一章课后习题及答案总结
- Xray and Burp linked Mining
- C language file operation
- Sqqyw (indifferent dot icon system) vulnerability recurrence and 74cms vulnerability recurrence
- Matplotlib绘图快速入门
猜你喜欢
Network layer - simple ARP disconnection
Attack and defense world misc practice area (simplerar, base64stego, no matter how high your Kung Fu is, you are afraid of kitchen knives)
captcha-killer验证码识别插件
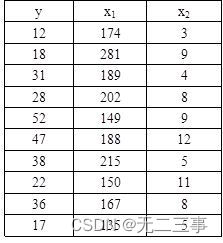
Statistics 8th Edition Jia Junping Chapter 12 summary of knowledge points of multiple linear regression and answers to exercises after class
图书管理系统

JVM memory model concept
1.支付系统

《英特尔 oneAPI—打开异构新纪元》
Statistics, 8th Edition, Jia Junping, Chapter 11 summary of knowledge points of univariate linear regression and answers to exercises after class

Network technology related topics
随机推荐
MySQL中什么是索引?常用的索引有哪些种类?索引在什么情况下会失效?
Bing Dwen Dwen official NFT blind box will be sold for about 626 yuan each; JD home programmer was sentenced for deleting the library and running away; Laravel 9 officially released | Sifu weekly
浙大版《C语言程序设计实验与习题指导(第3版)》题目集
Hcip -- MPLS experiment
Data mining - a discussion on sample imbalance in classification problems
Sqqyw (indifferent dot icon system) vulnerability recurrence and 74cms vulnerability recurrence
Mysql的事务是什么?什么是脏读,什么是幻读?不可重复读?
《英特尔 oneAPI—打开异构新纪元》
Solutions to common problems in database development such as MySQL
Apache APIs IX has the risk of rewriting the x-real-ip header (cve-2022-24112)
Windows platform mongodb database installation
Xray and burp linkage mining
内网渗透之内网信息收集(三)
图书管理系统
Binary search tree concept
《统计学》第八版贾俊平第三章课后习题及答案总结
数字电路基础(三)编码器和译码器
Intranet information collection of Intranet penetration (2)
Chain team implementation (C language)
Sword finger offer 23 - print binary tree from top to bottom