当前位置:网站首页>Statistics 8th Edition Jia Junping Chapter 10 summary of knowledge points of analysis of variance and answers to exercises after class
Statistics 8th Edition Jia Junping Chapter 10 summary of knowledge points of analysis of variance and answers to exercises after class
2022-07-06 14:30:00 【No two or three things】
Catalog
One 、 Knowledge framework
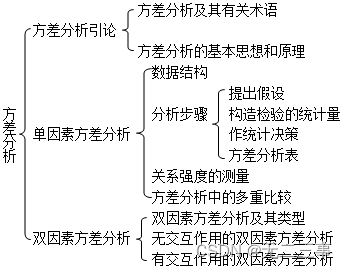
Two 、 After-school exercises
1 from 3 Sample data with different sampling capacity in each population , The results are shown in the table .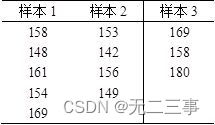
test 3 Is there a significant difference between the average values of the populations (α=0.01).
Explain : set up 3 The average values of the two populations are μ1,μ2,μ3.
suggest a hypothesis :H0:μ1=μ2=μ3,H1:μ1,μ2,μ3 Not exactly equal .
from Excel Output ANOVA table , As shown in the table .

because P-value=0.040877>α=0.01( or F=4.6574<F0.01(2,9)=8.0215), Don't reject the original assumption , There is no evidence 3 There are significant differences between the average values of the populations .
2 A home appliance manufacturing company is going to buy a batch 5 Battery No , existing A,B,C Three battery manufacturers are willing to supply , To compare the quality of the batteries they produce , Randomly selected from each enterprise 5 Battery only , Its service life is obtained through test ( Company :h) The data are shown in the table .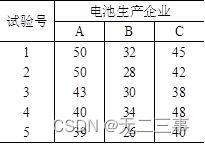
Try to analyze whether there is a significant difference between the average life of batteries produced by the three enterprises .(α=0.05) If there is a difference , use LSD Methods to test which enterprises have differences .
Explain : set up 3 The average life of batteries produced by enterprises are μA,μB,μC.
suggest a hypothesis :H0:μA=μB=μC;H1:μA,μB,μC Not exactly equal .
from Excel Output ANOVA table , As shown in the table 10-8、10-9 Shown .

surface 10-8

surface 10-9 Analysis of variance
because P-value=0.0003<α=0.05( or F=17.0684>F0.05(2,12)=3.8853), Rejection of null hypothesis , It shows that there is a significant difference between the average life of batteries .
In order to judge which two enterprises have significant differences in the average service life of batteries , First put forward the following assumptions :
test 1:H0:μA=μB;H1:μA≠μB.
test 2:H0:μA=μC;H1:μA≠μC.
test 3:H0:μB=μC;H1:μB≠μC.
Calculate the test statistics :
|xA-xB|=|44.4-30|=14.4
|xA-xC|=|44.4-42.6|=1.8
|xB-xC|=|30-42.6|=12.6
According to the ANOVA table 10-9 You know ,MSE=18.03333. According to degrees of freedom =n-k=15-3=12, check t The distribution shows that tα/2=t0.025=2.179. Because the sample size of each sample is 5, therefore

because |xA-xB|=14.4>LSD=5.85, Rejection of null hypothesis . therefore , Enterprises A And enterprises B There is a significant difference between the average service life of batteries ;
because |xA-xC|=1.8<LSD=5.85, Don't reject the original assumption . therefore , There is no evidence that the enterprise A And enterprises C There is a significant difference between the average service life of batteries ;
because |xB-xC|=12.6>LSD=5.85, Rejection of null hypothesis . therefore , Enterprises B And enterprises C There is a significant difference between the average service life of batteries .
3 The manager of a product manufacturing company wants to compare A,B,C Whether the three training methods have a significant impact on the product assembly time , take 20 New employees are randomly assigned to these three training methods . After training , The time spent by the employees participating in the training to assemble a product is shown in the table
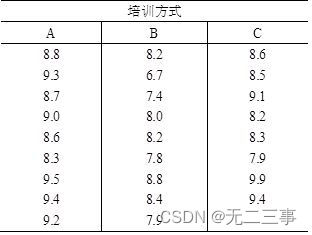
Take the significance level α=0.05. Determine whether different training methods have a significant impact on the time of product assembly ?
Explain : set up 3 The average time spent in assembling products by training methods is μA、μB、μC.
suggest a hypothesis :H0:μA=μB=μC;H1:μA、μB、μC Not exactly equal
from Excel Output ANOVA table , As shown in the table .

because P-value=0.00196<α=0.05( or F=8.2745>F0.05(2,23)=3.4221), Rejection of null hypothesis . It shows that different training methods have a significant impact on product assembly .
4 An enterprise is going to assemble a new product in three ways , To determine which method produces the most products per hour , Randomly selected 30 workers , And designate everyone to use one of these methods . The following results are obtained by variance analysis of the number of products produced by each worker , As shown in the table .

requirement :
(1) Complete the above ANOVA table .
(2) If the significance level α=0.05, Check whether there is a significant difference between the number of products assembled by the three methods .
Explain :(1) from Excel The missing values in the ANOVA table can be obtained , As shown in the table .
(2) From the analysis of variance table :P-value=0.245946>α=0.05( or F=1.478<F0.05(2,27)=3.554131), The original hypothesis cannot be rejected , That is, there is no evidence that 3 There is a significant difference between the number of products assembled by the two methods .
5 Yes 5 Grow seeds of different varieties and 4 Different fertilization schemes , stay 20 On a piece of land of the same area , take 5 Plant seeds and 4 Three fertilization schemes were combined to carry out the experiment , The harvest data obtained are shown in the table .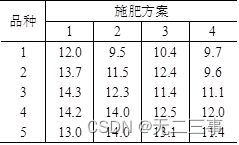
Test whether the effect of different varieties of seeds on the harvest is significant , Whether the effect of different fertilization schemes on the harvest is significant (α=0.05).
Explain : Let the average harvest of seeds of different varieties be μ1,μ2,μ3,μ4,μ5.
suggest a hypothesis :H0:μ1=μ2=μ3=μ4=μ5,H1:μ1,μ2,μ3,μ4,μ5 Not exactly equal
Set the average harvest of different fertilization methods as μ1,μ2,μ3,μ4.
suggest a hypothesis :H0:μ1=μ2=μ3=μ4,H1:μ1,μ2,μ3,μ4 Not exactly equal
from Excel The output ANOVA table is shown in the table .
because P-value=0.0033<α=0.05( or F seeds =7.2397>F0.05(4,12)=3.2592), Rejection of null hypothesis . It shows that there are significant differences in the effects of seeds of different varieties on the harvest .
P-value=0.0019<α=0.05( or F Fertilization program =9.2047>F0.05(3,12)=3.4903), Rejection of null hypothesis . It shows that there are significant differences in the effects of different fertilization schemes on the harvest .
6 To study whether the packaging method and sales area of food have an impact on its sales , It is sold in three different regions with three different packaging methods , The obtained sales volume data is shown in the table .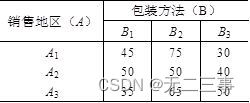
Test whether different regions and different packaging methods have a significant impact on the sales volume of the food .(α=0.05)
Explain : Let the average sales volume in different regions be μA1,μA2,μA3.
suggest a hypothesis :H0:μA1=μA2=μA3,H1:μA1,μA2,μA3 Not exactly equal .
Set the average sales volume of different packages as μB1,μB2,μB3.
suggest a hypothesis :H0:μB1=μB2=μB3,H1:μB1,μB2,μB3 Not exactly equal .
from Excel The output ANOVA table is shown in the table .
because P-value=0.9311>α=0.05( or F region =0.0727<F0.05(2,4)=6.9443), Don't reject the original assumption . There is no evidence that different regions have a significant impact on the sales of this food .
P-value=0.1522>α=0.05( or F Packing method =3.1273<F0.05(2,4)=6.9443), Don't reject the original assumption . There is no evidence that different packaging methods have a significant impact on the sales of this food .
7 A supermarket chain conducted a study , Determine whether the location of the supermarket and the number of competitors have a significant impact on sales .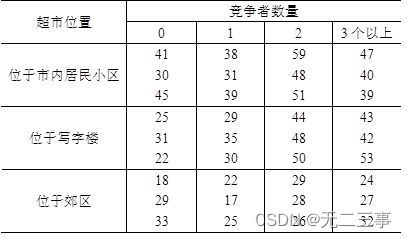
Take the significance level α=0.01, test :
(1) Whether the number of competitors has a significant impact on sales .
(2) Whether the location of the supermarket has a significant impact on sales .
(3) Whether the number of competitors and the location of supermarkets have an interactive impact on sales .
Explain : from Excel The output ANOVA table is shown in the table .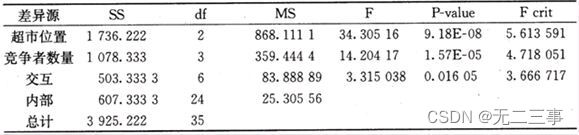
(1) suggest a hypothesis :
H0: The number of competitors has no significant impact on sales
H1: The number of competitors has a significant impact on sales
because P-value=1.57E-5<α=0.01( or F The number of competitors =14.2042>F0.01(3,24)=4.7181), Rejection of null hypothesis . It shows that the number of competitors has a significant impact on sales .
(2) suggest a hypothesis :
H0: The location of supermarkets has no significant impact on sales
H1: The location of supermarkets has a significant impact on sales
P-value=9.18E-08<α=0.01( or F Supermarket location =34.3052>F0.01(2,24)=5.6136), Rejection of null hypothesis . It shows that the location of supermarkets has a significant impact on sales .
(3) suggest a hypothesis :
H0: The number of competitors and the location of supermarkets have no interactive effect on sales
H1: The number of competitors and the location of supermarkets have an interactive impact on sales
P-value=0.01605>α=0.01( or F Interaction =3.3150<F0.01(6,24)=3.6667), Don't reject the original assumption . There is no evidence that the number of competitors and the location of supermarkets have an interactive effect on sales .
边栏推荐
- HackMyvm靶机系列(1)-webmaster
- 《统计学》第八版贾俊平第五章概率与概率分布
- On the idea of vulnerability discovery
- 《统计学》第八版贾俊平第七章知识点总结及课后习题答案
- Strengthen basic learning records
- Intranet information collection of Intranet penetration (I)
- Based on authorized access, cross host, and permission allocation under sqlserver
- JDBC事务、批处理以及连接池(超详细)
- Lintcode logo queries the two nearest saplings
- Experiment 9 input and output stream (excerpt)
猜你喜欢
Ucos-iii learning records (11) - task management
WEB漏洞-文件操作之文件包含漏洞
List and data frame of R language experiment III
Detailed explanation of network foundation routing

Binary search tree concept

网络基础之路由详解
Hackmyvm target series (3) -visions

Constants, variables, and operators of SystemVerilog usage
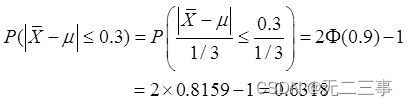
《统计学》第八版贾俊平第六章统计量及抽样分布知识点总结及课后习题答案
内网渗透之内网信息收集(二)
随机推荐
The most popular colloquial system explains the base of numbers
内网渗透之内网信息收集(四)
Wei Shen of Peking University revealed the current situation: his class is not very good, and there are only 5 or 6 middle-term students left after leaving class
Harmonyos application development -- address book management system telmanagesys based on listcontainer [phonebook][api v6]
《统计学》第八版贾俊平第三章课后习题及答案总结
Experiment five categories and objects
Ucos-iii learning records (11) - task management
Intranet information collection of Intranet penetration (I)
Xray and Burp linked Mining
JVM memory model concept
The difference between layer 3 switch and router
Attack and defense world misc practice area (simplerar, base64stego, no matter how high your Kung Fu is, you are afraid of kitchen knives)
《统计学》第八版贾俊平第二章课后习题及答案总结
Record once, modify password logic vulnerability actual combat
Intranet information collection of Intranet penetration (5)
小程序web抓包-fiddler
How does SQLite count the data that meets another condition under the data that has been classified once
JDBC事务、批处理以及连接池(超详细)
Only 40% of the articles are original? Here comes the modification method
链队实现(C语言)