Chapter 16 intensive learning

1. Analyze the connection and difference between reinforcement learning and supervised learning .

What a machine has to do is to learn one by constantly trying in the environment " Strategy " (policy) $\pi$, According to this strategy , In state $x$ Next, you can know what action to perform $\alpha =\pi (x)$, For example, when you see that the melon seedling state is lack of water , Can return to action " watering ". There are two ways to represent a strategy : One is to represent the strategy as a function $\pi :X\mapsto A$, Deterministic strategies are often expressed in this way ; The other is probability representation $\pi :X\times A\mapsto \mathbb{R}$
Randomness strategy is often expressed in this way ,$\pi (x,a)$ For state $x$ Choose action $a$ Probability , It has to be here ${\sum }_a^{}\pi (x,a)=1$.

If the " state " It corresponds to " Example "、“ action " Corresponding to " Mark " You can see , Strengthen learning " Strategy " In fact, it is equivalent to supervising learning " classifier ” ( When the action is discrete ) or " Regressor " ( When the action is continuous , There is no difference in the form of the model . But the difference is , In reinforcement learning, there is no labeled sample in supervised learning ( namely " Example - Mark " Yes ) , In other words , No one directly tells the machine what action it should do under what state , Only when the final result is announced , Can pass " reflection " Whether the previous action is correct to learn . therefore , Reinforcement learning can be regarded as having " Delay flag information " The problem of supervised learning .

2. $ϵ$- How can the greedy method achieve the balance between exploration and utilization .

$ϵ$- The greedy method is based on a probability to make a compromise between exploration and utilization ： Every time you try , With $ϵ$ To explore the probability of , In other words, a rocker arm is randomly selected with uniform probability ; With $1-ϵ$ The use of probability , That is to choose the one with the highest average reward at present .

If the uncertainty of rocker arm reward is large , For example, when the probability distribution is wide , More exploration is needed , At this time, a larger $ϵ$ value ; If the uncertainty of the rocker arm is small , For example, when the probability distribution is relatively concentrated , Then a few attempts can well approximate the real reward , What is needed at this time $ϵ$ smaller . Usually make $ϵ$ Take a smaller constant , Such as 0.1 or 0.01. However , If the number of attempts is very large , So after a period of time , The rewards of the rocker arm can be well approximated , No need to explore , In this case $ϵ$ As the number of attempts increases, it gradually decreases , For example, Ling $ϵ=1/\sqrt{t}$.

3. How to use gambling machine algorithm to realize reinforcement learning task .

Different from general supervised learning , The final reward of reinforcement learning task can only be observed after multi-step action . Reinforcement learning is significantly different from supervised learning , Because the machine tries to find the results of each action , There is no training data to tell the machine which action to do .

Consider simpler situations ： Maximize one-step rewards , That is, consider one-step operation . actually , One step reinforcement learning task corresponds to a theoretical model , namely “K- Swing arm gambling machine ”. As shown in the figure below ,K- There are K A rocker arm , After putting in a coin, the gambler can choose to press one of the rocker arms , Each rocker gives out a coin with a certain probability , But this probability gambler doesn't know . The goal of gamblers is to maximize their rewards through certain strategies , That is to get the most coins .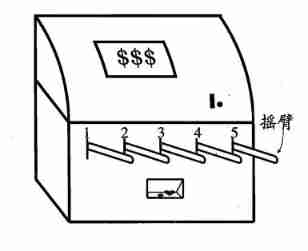
If only to know the expected reward of each rocker arm , You can use “ Just explore ” Law ： Distribute all the trial opportunities equally to each rocker arm , Finally, the average payout probability of each rocker arm is taken as the approximate estimation of its reward expectation . If only to perform the action with the greatest reward , You can use “ Use only ” Law ： Press the best rocker arm at present , If there are more than one rocker arm, it is optimal , Then randomly choose one of them . obviously ,“ Just explore ” The method can estimate the reward of each rocker arm very well , But you will lose a lot of opportunities to choose the best rocker arm ;“ Use only ” The law is the opposite , It doesn't expect rewards well , It is likely that the optimal rocker arm is often not achieved . therefore , Neither of these methods can maximize the final cumulative reward . obviously , If you want to accumulate the most rewards , We must reach a good compromise between exploration and utilization .

4. Trial derivation The full probability expansion of discount cumulative reward (16.8).

When the model is known , For any strategy $\pi$ Can estimate the expected cumulative rewards brought by this strategy . Let function $V^{\pi }(x)$ Represents slave state $x$ set out , Executive action $a$ Then use the strategy $\pi$ Cumulative rewards ; function $Q^{\pi }(x,a)$ Represents slave state $x$ set out , Executive action $a$ Then use the strategy $\pi$ Cumulative rewards . there $V(\cdot )$ be called “ State value function ”,$Q(\cdot )$ be called “ state - Action value function ”, Respectively means to specify “ state ” And specify “ state - action ” Cumulative rewards on .

By the definition of cumulative rewards , Stateful valued function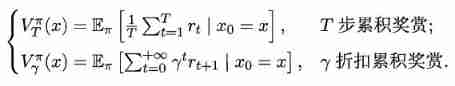

Make $x_0$ Indicates the starting state ,$a_0$ Indicates the first action taken in the initial state ; about $T$ Step to accumulate rewards , Use subscript $t$ Indicates the number of subsequent steps . We are in a state - Action value function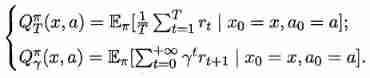

because MDP It has Markov property , That is, the state of the system at the next time is only determined by the state at the current time , Not dependent on any previous state , So the value function has a very simple recursive form . about $T$ Step cumulative rewards are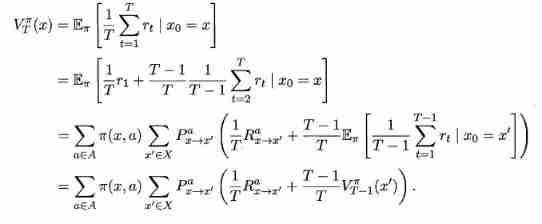

Allied , about $\gamma$ The cumulative rewards of discounts are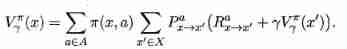

Here's the thing , Formally due to $P$ and $R$ It is known that , Then the full probability expansion can be carried out .

5. What is the optimality principle in dynamic programming , What does it have to do with strategy updating in reinforcement learning

The key of the dynamic method is to correctly summarize the basic recurrence relations and appropriate boundary conditions . Do that , The problem process must first be divided into several interrelated stages , Properly select state variables and decision variables and define the optimal value function , Thus, a big problem can be transformed into a group of sub problems of the same type , Then solve them one by one . That is, starting from the boundary conditions , Step by step recursive optimization , In the solution of each subproblem , Both use the optimization results of its front subproblem , In turn , The optimal solution of the last subproblem , Is the optimal solution of the whole problem .

Reinforcement learning can refer to the idea of dynamic programming , Just maximize the reward for each step , Can achieve the goal of maximizing cumulative rewards .

6. Complete timing difference learning Chinese (16.31) The derivation of .

The essence of Monte Carlo reinforcement learning , It is an approximation of the expected cumulative reward by averaging after many attempts , But when it is averaged, it is “ Batch processing ” On going , That is, after a complete sampling track is completed, all States - Action update . In fact, this update process can be carried out incrementally . For the State - The action is right $(x,a)$, It may be assumed that based on $t$ Samples have estimated the value function $Q_t^{\pi }(x,a)=\frac{1}{t}{\sum }_{i=1}^t{r}_i$, Then get the $t+1$ Individual sampling $r_{t+1}$ when , Yes ：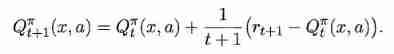

obviously , Just give $Q_t^{\pi }(x,a)$ Plus the increment $\frac{1}{t+1}(r_{(}t+1)-Q_t^{\pi }(x,a))$.
A more general , take $\frac{1}{t+1}$ Replace with a coefficient ${\alpha }_{t+1}$, The incremental item can be written $\alpha (r_{t+1}-Q_t^{\pi }(x,a))$.

With $\gamma$ Take discount cumulative rewards as an example , Use the dynamic programming method and consider the use of state when the model is unknown - Action value function is more convenient , Available ：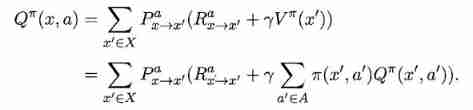

By incremental summation ：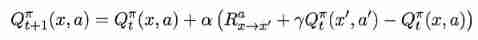

among $x^{{}^{\prime }}$ It was the last time in the state $x$ Executive action $a$ After the transition to the state of ,$a^{{}^{\prime }}$ It's a strategy $\pi$ stay $x^{{}^{\prime }}$ Action selected on .

7. For goal driven reinforcement learning tasks , The goal is to reach a certain state , For example, the robot walks to the predetermined position , Suppose the robot can only move in one-dimensional space , That is, it can only move left or right , The starting position of the robot is on the far left , The predetermined position is on the far right , Try to set reward rules for such tasks , And programming .

( Procedure reference ：https://github.com/MorvanZhou/Reinforcement-learning-with-tensorflow/blob/master/contents/1_command_line_reinforcement_learning/treasure_on_right.py)