The beauty of Mathematics -- the principle of fine Fourier transform

Catalog

One 、 Fourier series （Fourier Series、FS） Real field representation of

Two 、 Fourier series （Fourier Series、FS） The complex field of

3、 ... and 、 The Fourier transform （FT） The introduction of

Four 、DTFT、DFT、FFT The introduction of

---

First time to know Fourier （Fourier） It was in my sophomore year 《 Signals and systems 》 In class , At that time, I didn't know the use of this course , What I heard was also stunned .. In the end, I just wrote down some formulas three days before the end of the term , Be able to test the level , At first, I thought that I would never touch the ghost of communication again ,, Who wanted to , Four years later , After going to graduate school, I began to communicate by mistake , Looking back and savoring the Fourier transform learned four years ago, it suddenly became clear , Suddenly I feel that mathematics is really the most romantic subject of science and Engineering （ One of them. ）！

There may be many coincidences in the world , But the only tool that can perfectly combine these coincidences and form a perfect theory may be Mathematics , This may be the romance and profundity of Mathematics ~

• Yes Periodic continuity Function to triangulate , This process is called  FS（ Fourier series ）
• When the period tends to infinity , That is, the function becomes Aperiodic continuous when ,FS It becomes FT（ The Fourier transform ）
• In engineering application , Yes Aperiodic continuous Function is discretized in time domain （ Sampling ）, Turn into Aperiodic discrete function ,FT becomes DTFT（ Discrete time Fourier transform ）
• Yes Aperiodic discrete The delay extension of the function becomes Periodic discretization function , DTFT becomes DFT（ Discrete Fourier transform ）
• DFT The computational complexity is high , Yes DFT Of Optimize the calculation method , DFT becomes FFT（ The fast Fourier transform ）

Visible Fourier series （FS） yes FT、DTFT、DFT、FFT The basis of , The following transformations are all in FS Derived from the basic principle of , therefore , Clearly understand FS The basic principle of is very important , Therefore, this article focuses on FS Principle .

One 、 Fourier series （Fourier Series、FS） Real field representation of

Did you learn 《 Advanced mathematics 》 My friends must all know one called   Taylor's series   Things that are ：

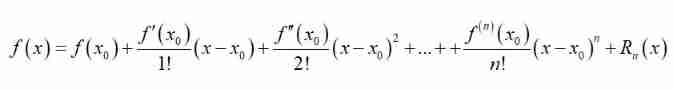
The principle of this thing is to use Power series To represent a function in A point x0 The neighborhood of Decomposition within . comparison Fourier series The difference is that it can only be used to represent the expansion in the neighborhood of a certain point of the function , And the power function is The base , But both involve decomposing the signal into Simple signals Linear combination of .

Similar to Taylor series , Fourier series Is a kind of right Periodic signal ( Periodic function ) Decomposition representation of , It consists of one to one harmonic Relational Trigonometric functions Of Weighted addition To represent a periodic signal . In particular , If a function is a periodic function , Then it can be decomposed into sine function and cosine function The base The linear combination of . If the function f(t) Yes, the period is T The periodic function of , Then its Fourier series expansion is as follows ：

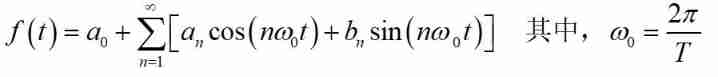
  In the formula ,  It is called fundamental frequency ,  Is harmonic frequency . Specially ,a0 Is the DC component , Can be seen as a0=a0cos(0).

Now the formula of Fourier series has , But there are problems （ Take notes ！）：

1、 Why is the function in the expansion , No matter cos still sin, It's all about For the fundamental wave ？ Can it be another value to do the fundamental wave ？

  answer ： This is easy to say ： Must be    As the fundamental wave of Fourier series . You want to , Only when the functions in the Fourier expansion are based on the fundamental wave Or harmonics    When it is angular frequency , The common period of each function is T（ For harmonic components ,T/n Is its minimum period , but T It is also a cycle ）, In this way, the period of the result after linear combination will still be T. If I go the other way , Add a period to many expansions as T1 ≠ T Components of , Obviously, the period of the result of such a linear combination will never be T 了 , It cannot be expressed f(t) 了 .

2、 Given a periodic signal , How do I choose to use cos Or use sin Or both are used to expand the Fourier series of the signal ？

answer ： This is easy to explain .cos It's even function ,sin It's an odd function . Obviously , When f(t) When it's an even function , Just use cos Function FS an ; When f(t) When it's an odd function , Just use sin Function FS an ; When f(t) Non odd and non even , Because it necessarily It can be decomposed into the sum of an odd function and an even function ：

therefore , At this time need cos and sin Together with FS an . 

3、 How to calculate FS The coefficient of an And bn ？

answer ： It's not hard . Popular point theory ,an as well as bn The physical meaning of the value of is the characterization function  f(x) And    as well as    The degree of similarity （ Or the degree of relevance ）. let me put it another way ,an as well as bn The value of represents    as well as    In the process of linear combination, the result  f(t) Contribution of .

You can taste this sentence qualitatively ： If f(x) Images and    perhaps    A function in looks like , That means the image Coincident part More , Then the    perhaps    The weight of the component will naturally be larger , This should be easy to understand , Reflect on FS The middle is  an perhaps bn Is larger . Imagine an extreme example , If  , Then its Fourier transform FS = , In addition to a1 = 1 outside , Other values are 0, This is also determined by the orthogonality of trigonometric functions .

So how to calculate the specific value quantitatively ？ And that's where it comes in relevant The concept of .

For signals f1 And signals f2 The relevant mathematical definitions of are as follows （ Pay attention to the difference between convolution ）：

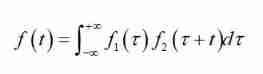
  For a more intuitive understanding of , You can use the following figure to illustrate . In the figure is the image of two functions .

chart 1 Image of two functions that perform correlation operations

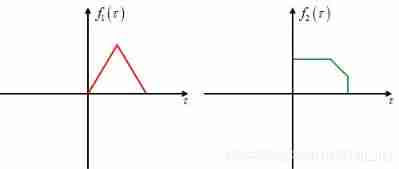
    Do correlation operations on these two functions , give the result as follows ：

chart 2 Diagram of correlation operation with phase difference

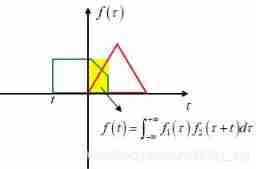
In the figure Multiply the values of the green region of the two functions ( Note that it is not the intersection area ！) It is the result of correlation operation , among , Variable t It can be seen in two functions ( Add... On the basis of the original phase difference ) Of Phase difference , When the phase difference is 0 when , The results of the correlation operation are as follows ：

chart 3 The phase difference is 0 Relevant operation diagram of

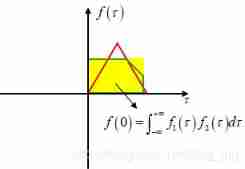
It's not difficult to understand. , For Fourier series , Original signal f(t) And    And    The way of related operation is graph 3 The paradigm in . If you just want to know FS Principle , Just see here , If you still want to get the final specific results, then continue to look down .

We are very sensitive to the original signal f(t) In one cycle to    Find integral , And by trigonometric function Orthogonality （ The trigonometric function term of Fourier series is actually an orthogonal function system ） You know ：

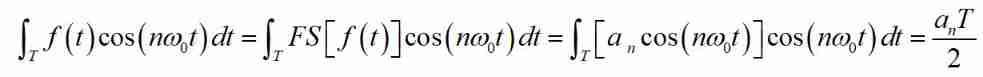
  It can be concluded that :

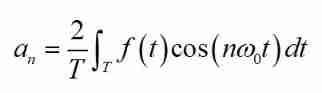
Empathy ：

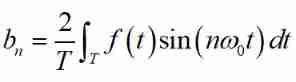
Specially , When n=0 when ,sin0=0,cos0=1, here

this time  an as well as bn The value of is also solved .

The form of the above Fourier series contains zero phase difference of the same frequency sin And cos component , The frequency of sine and cosine components of the same frequency will not change after superposition , Therefore, the distribution of spectrum and phase cannot be directly reflected . Sine and cosine components are essentially the same , It's just the phase difference 90° nothing more . At this time , In order to present the spectrum more intuitively , It is necessary to set the same frequency  cos And sin A merger ：

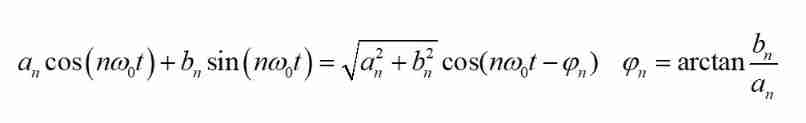
  And you can see , The amplitude and phase at the frequency are determined by the sine component and cosine component at the frequency , here FS It can be rewritten as follows ：

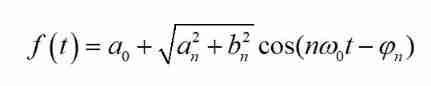
This formula intuitively reflects f(t) Spectrum component and its proportion .

thus , The real number domain calculation of Fourier series is completed .

Two 、 Fourier series （Fourier Series、FS） The complex field of

In practical signal analysis problems , The signals we encounter are often complex signals （ There is no complex signal in nature , But in Operational analysis Complex signals can be used in the process Express To simplify the calculation ）, But the above analysis only applies to the signal form in the real number domain . Is there a FS The form can be used for the operation of real number field and complex number field at the same time ？ The answer is yes , Now we have to draw out a most coquettish formula of the universe —— Euler formula ：

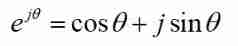
Many people may ask ： What is the meaning of this formula written like this ？ In fact, this formula is just a tool from the perspective of Mathematical Application , It is a form of artificial definition , In the formula  j The specific significance of should be analyzed in the specific use environment , You can analyze it from various angles , For example, in mathematical operations ,j It means -1 The square root of ; In the field of signal processing ,j It represents one in the complex plane Rotation operator . As for how to get this formula , The answer is what the article said at the beginning —— coincidence , It happens to be this form , It happens to be right to calculate with this rule , It happens that this calculation is the most perfect ... This is the beauty of Mathematics , I have to admire Euler's imagination .

With this formula , You can use the plural to express cos And sin Function ：

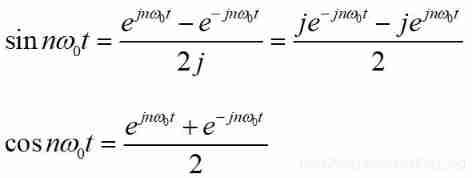
  Bring this conclusion to the above FS Simplify in the formula , We can deduce the more general expansion of Fourier series ：

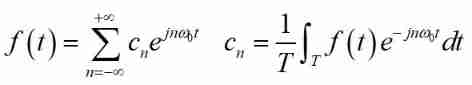
there    It's a signal  f(t) Corresponding spectrum . hypothesis f(t) Is a real function , Let's proceed to the complex field FS  Reverse derivation of , The surprise brought by this beautiful coincidence is about to appear （^-^）！

  First of all, will    Plug in , have to ：

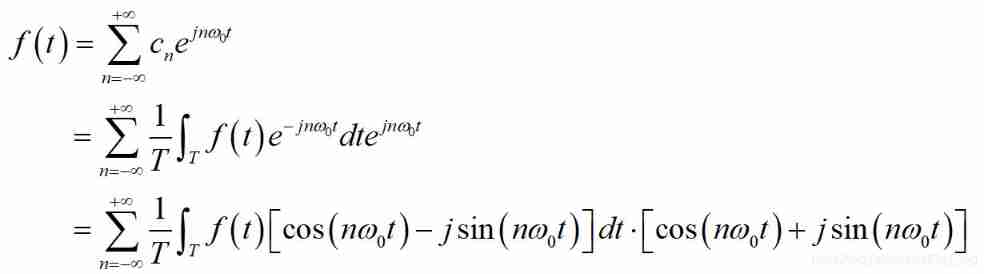
  Then for the convenience of calculation , Replace with the following variables ：

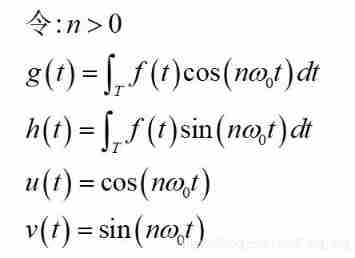
After replacement ：

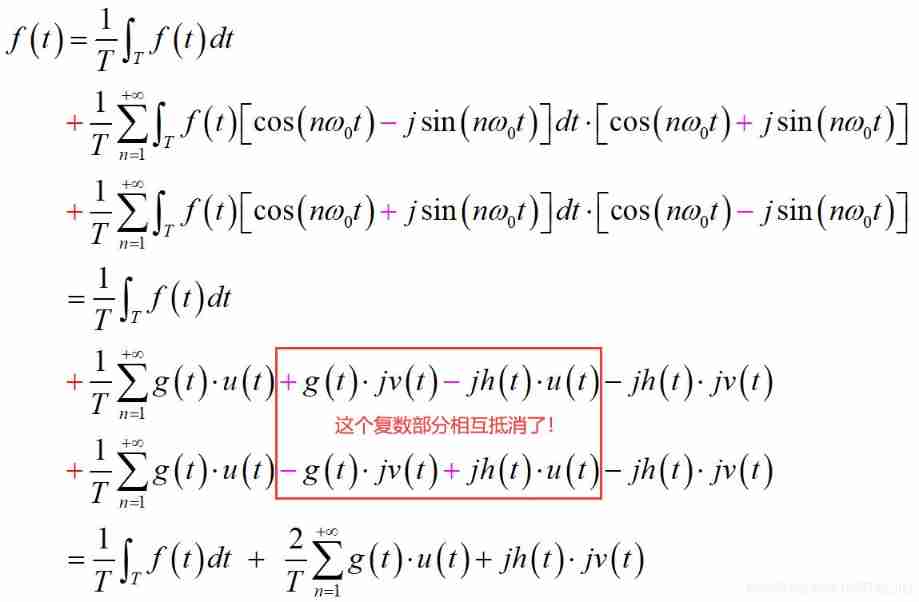
Replace the variable back to get ：

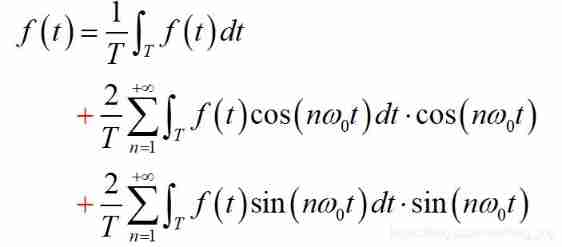
  Now I'm going back to the first part FS In the field of real numbers, we have to make a comparison , Just ask you if you are magical hahaha

3、 ... and 、 The Fourier transform （FT） The introduction of

  Fourier series is right Periodic continuity Decomposition by function , But almost all signals in nature are aperiodic continuous signals , So we need to expand Fourier series , Let's first look at the spectrum calculation formula of the complex field of Fourier series above ：

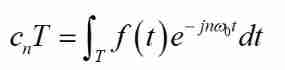
  We can regard aperiodic functions as functions with infinite periods , because , With T The increase of , Spectral interval    Infinitely smaller , Finally, it becomes a continuous spectrum , At this moment Discrete spectrum It becomes Continuous spectrum , The envelope expression of the spectrum becomes ：

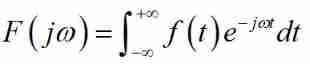
This expression is The Fourier transform (FT) The expression of .

And the original FS Of Discrete spectral coefficients It can be obtained from the continuous spectrum ：

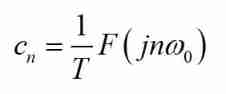
Empathy , Its inverse transformation At this point, it becomes ：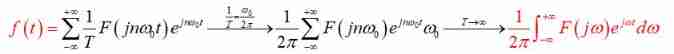

Four 、DTFT、DFT、FFT The introduction of

DTFT、DFT、FFT These three algorithms are extensions of Fourier transform in engineering applications . stay Engineering applications in , It is certainly unrealistic to forcibly calculate the spectrum of signals by hand , Generally, computers are needed for auxiliary calculation .FS And FT It's all in Simulation domain Calculate the spectrum of the signal , But computers can only handle Digital domain The discrete signal of the , Therefore, continuous analog domain signals must be converted to discrete digital domain by sampling in order to be processed by computer , That's what you need to use DFT, But in DFT There was an intermediate process before , Namely DTFT.

DTFT Only the time domain is discretized , The Fourier transform pair formula is as follows ：

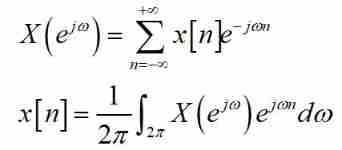
It can be seen that , here although DTFT The time domain is discrete , But its frequency domain （ spectrum ） Still continuous Of , And if you want the computer to calculate smoothly , The spectrum must also be discrete , Therefore, it is also necessary to discretize the frequency domain , This is it. DFT,DFT The transformation formula is as follows ：

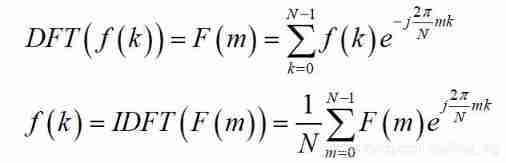
We discretize the time domain into N A little bit , And the time delay is expanded into a periodic function , This is the time for N Dot DFT Calculation will get  N Spectrum output of points .（ This involves a knowledge point ： Time domain periodic discretization Corresponding Discrete period in frequency domain , Because this article mainly involves the explanation of engineering principles , This will not be discussed ）

Further , Due to the direct use of computers DFT The time complexity is too high [ O(n²) ], So you need to DFT The calculation is accelerated , The optimized DFT Calculation method [ O(nlogn) ] Fast Fourier Algorithm , namely FFT.

==============================================================

Related connection （ The following links look easy to understand ）：

https://www.cnblogs.com/abella/articles/9770989.html

https://www.zhihu.com/question/23234701/answer/26017000

https://www.bilibili.com/video/BV1Tb41187i1